根據前面的分析,電子或者空穴產生于導帶和價帶中是一個統計概率,這個概率符合費米分布規律。
所以雖然前文推導出了在某個能級的電荷濃度準確表達式,但實際上這是一個統計算法,其描述的是一個動態平衡過程。具體到每一個能級及其相應的能態,則是電子在不斷的產生和消失的過程中處于平衡狀態。
這個過程與環境溫度和材料本身的性質相關,教科書中通常將這個過程理解為:由于熱運動,電子獲得能量而激發到能量更高的能級;但電子彼此碰撞、或者與晶格碰撞等過程失去能量又回到能量更低的能級,這個過程持續往復。
更進一步地,考慮半導體中摻入了某種雜質、或者引入了某種缺陷的情況。雜質或缺陷的引入導致在禁帶之中形成了局域的能級,因為這些能級相較導帶及價帶的能級離費米能級更近,所以電子占有概率更大。同時,因為能態密度較低,占據這些能級的電子是不能自由運動的,表現為電荷減少,被“復合”了。
結合質量守恒定律,有一種理解方式如下:材料自身在單位體積內能夠提供的電子數量是一定的,假設一個原子提供一個電子,那么材料可以提供的總電子數量即為


當占據雜質或缺陷能級消耗了一部分電子,那么激發到導帶上的電子自然少了,表現為電子被雜質或缺陷能級復合了。
事實上,若要嚴謹推導半導體中摻雜后的復合現象,還是要從雜質引入所導致的能級變化和能態變化來分析電子占據不能能級的概率,這里不做延展推導。
想要說明的是,類似空穴是人們抽象出來的一個概念一樣,“復合”也可以當做人們抽象出來的一個概念,是相對“產生”而言,其本質還是因為某種原因如摻雜、缺陷等,導致能級和/或能態發生變化,導致電子在不同能級進行重新分布。
假如電子進入導帶,能級分布密集,能態很多,且基本沒有電子占據,那么 電子只需獲得很小的能量即可進入另外一個能態,電子占據這些能態后可以自由移動,表現為自由電荷的產生 。
假如進入雜質或缺陷能級,能態很少,電子需獲得較大的能量才可進入另外一個能態,那么電子占據這些能態后不能自由移動,表現為自由電荷的復合。
既然引入了復合的概念,那就應該有復合的壽命,定義為τ,這個壽命是如何得來,又是如何變化的,下面簡要推導。



顯然凈復合率U還可表達為

對照U的兩個表達式,可以得出電荷壽命

根據這個表達式,隨著新增電荷數的增加,電荷壽命會降低,所以 半導體大注入情況下比小注入情況下的壽命要小,IGBT工作通常處于大注入狀態。IGBT關斷過程中的拖尾電流通常取決于存儲的電荷及其壽命。
對于本征半導體,?n=?p=0,n 0 =p 0 =n i ,定義其載流子壽命為

對于p型摻雜半導體,p 0 >>n 0 ,這個濃度顯然是 僅與溫度相關的常數,不隨時間變化, 因為?n=?p,所以

兩邊對時間求導,且dp 0 /dt=dn 0 /dt=0

顯然上式成立的條件是τ p <<τ n ,即空穴壽命遠小于電子壽命。所以對于p型摻雜半導體可以僅考慮少子電子,其壽命為

同理,對于n型摻雜半導體,空穴為少子,其壽命為

顯然摻雜后的少子壽命都是要小于本征半導體的載流子壽命的。
-
半導體
+關注
關注
334文章
27010瀏覽量
216310 -
IGBT
+關注
關注
1265文章
3761瀏覽量
248312 -
電荷
+關注
關注
1文章
612瀏覽量
36108 -
載流子
+關注
關注
0文章
133瀏覽量
7645
發布評論請先 登錄
相關推薦
[專]電荷為何自發產生——第一彈
一種新型低電荷共享電荷泵電路
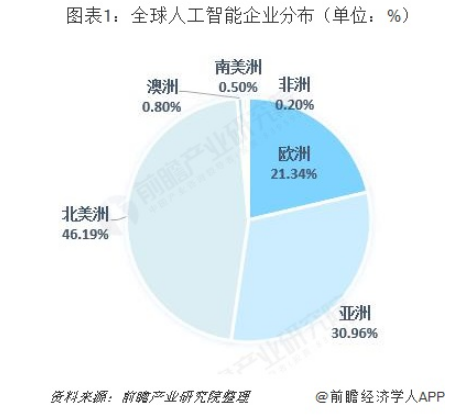
一文帶你解讀全球人工智能產業發展現狀
電容器存儲電荷的原理是怎樣的(一)
一文解讀FPGA設計者的5項基本功及設計流程資料下載





 一文解讀電荷的復合
一文解讀電荷的復合











評論