Part11. 圖像的邊緣

灰度圖像的分割算法大多都基于兩個性質(zhì)：灰度的不連續(xù)性和灰度的相似性。

對于不連續(xù)性的灰度，可以以灰度突變?yōu)榛A(chǔ)分割一幅圖像，比如通過圖像的邊緣，基于邊緣進(jìn)行圖像分割。對于相似的灰度，可以通過區(qū)域進(jìn)行圖像分割。本文主要介紹圖像邊緣相關(guān)的內(nèi)容和原理。

圖像的邊緣是圖像中亮度變化比較大的點(diǎn)。圖像邊緣點(diǎn)的出現(xiàn)一般是由于深度的不連續(xù)、物體表面方向的變換、物體屬性變化或者場景照明變化引起。

邊緣是連通的邊緣像素集合。

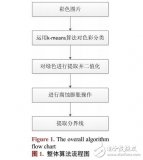
常見的邊緣類型有三種：

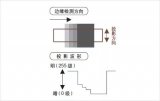
階梯形邊緣：即從一個灰度到比它高好多的另一個灰度。

屋頂形邊緣：它的灰度是慢慢增加到一定程度，然后慢慢減少。

線性邊緣：它的灰度從一個級別跳到另一個灰度級別之后然后回來。

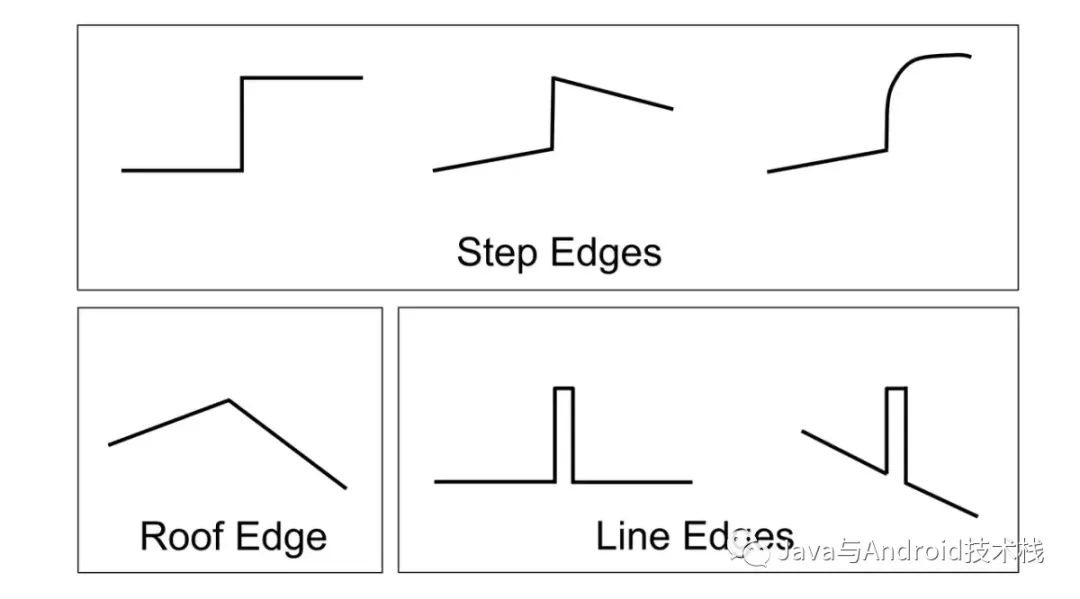常見的邊緣類型.PNG

真實(shí)的圖像邊緣可能含有噪聲，不一定符合上述理想的邊緣模型。

Part22. 圖像的梯度

圖像可以看成是一個二維離散函數(shù)，為了衡量圖像灰度的變化率，可以對二維離散函數(shù)進(jìn)行求導(dǎo)(連續(xù)的函數(shù)可以直接求導(dǎo)，離散的函數(shù)只能通過一些方法來近似)。一階或二階導(dǎo)數(shù)都可以檢測局部灰度突變。

12.1 差分

差分，又名差分函數(shù)或差分運(yùn)算，一般是指有限差分，是數(shù)學(xué)中的一個概念，將原函數(shù) f(x) 映射到 f(x+a) - f(x+b) 。

差分運(yùn)算，相應(yīng)于微分運(yùn)算，是微積分中重要的一個概念。差分對應(yīng)離散，微分對應(yīng)連續(xù)。

差分可分為前向差分、反向差分和中心差分。

2.1.1 前向差分

當(dāng)自變量從變到時，函數(shù)的改變量，稱為函數(shù) f(x) 在點(diǎn)的步長為 的一階(前向)差分。

通常記為，，其中為差分算子。

同理，為 處的二階差分。

為 處的 n 階差分。

2.1.2 反向差分

一階反向差分為：

2.1.3 中心差分

一階中心差分為：

22.2 導(dǎo)數(shù)

數(shù)字函數(shù)的導(dǎo)數(shù)可用有限差分定義。

首先，將 展開為 x 的泰勒級數(shù)，我們可以得到一維函數(shù) f(x) 在任意點(diǎn) x 處的一階導(dǎo)數(shù)的近似：

則：

當(dāng) 時

對于一階導(dǎo)數(shù)，我們只使用線性項(xiàng)，可得：

由此，用前向差分得到灰度差：

當(dāng) 時

對于一階導(dǎo)數(shù)，我們同樣只使用線性項(xiàng)，可得：

由此，用反向差分得到灰度差：

使用(2)式-(3)式，用中心差分可得：

中心差分的誤差較小，導(dǎo)數(shù)通常表示為中心差分。基于中心差分的二階導(dǎo)數(shù)，使用(2)式+(3)式，可得：

即：

通常，一階導(dǎo)數(shù)和二階導(dǎo)數(shù)對分析邊緣有以下的結(jié)論：

一階導(dǎo)數(shù)通常在圖像中產(chǎn)生較粗的邊緣；

二階導(dǎo)數(shù)對精細(xì)細(xì)節(jié)，如細(xì)線、孤立點(diǎn)和噪聲有較強(qiáng)的響應(yīng)；

二階導(dǎo)數(shù)在灰度斜坡和灰度臺階過渡處會產(chǎn)生雙邊緣響應(yīng)；

二階導(dǎo)數(shù)的符號可用于確定邊緣的過渡是從亮到暗還是從暗到亮。

計算圖像中每個像素位置的一階導(dǎo)數(shù)和二階導(dǎo)數(shù)的方法是空間卷積。

當(dāng)我們把圖像看做是一個二維離散函數(shù)時，通過上述方式可得 x、y 方向的二階導(dǎo)數(shù)：

以及

根據(jù)拉普拉斯算子，圖像可以定義為

由(5)式+(6)式，可得：

(7)式可寫成如下 filter mask 的形式 ：

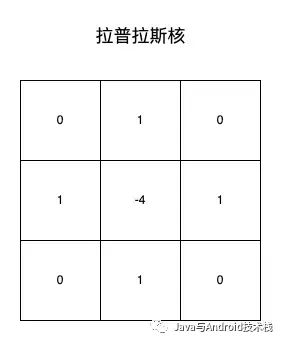laplace核.png

拉普拉斯可以對圖像進(jìn)行銳化，利用下面的公式：

其中，f(x,y) 表示原圖，g(x,y) 表示銳化后的圖像，c = -1，則

對于不同的拉普拉斯核，c 可能會取不同的值。

下面的代碼，展示了對灰度圖像進(jìn)行銳化以及對灰度圖像的拉普拉斯變換：

#include
#include
#include

usingnamespacestd;
usingnamespacecv;

intmain(intargc,char*argv[])
{
Matsrc=imread(".../girl.jpg");
imshow("src",src);

Matgray;
cvtColor(src,gray,COLOR_BGR2GRAY);
imshow("gray",gray);

Matdst,laplace;

dst.create(src.size(),CV_8UC1);
laplace.create(src.size(),CV_8UC1);

intheight=gray.rows;
intwidth=gray.cols;

for(inti=1;i(i,j)=saturate_cast(5*gray.at(i,j)-gray.at(i+1,j)-gray.at(i-1,j)-gray.at(i,j+1)-gray.at(i,j-1));
laplace.at(i,j)=saturate_cast(gray.at(i+1,j)+gray.at(i-1,j)+gray.at(i,j+1)+gray.at(i,j-1)-4*gray.at(i,j));
}
}
imshow("dst",dst);
imshow("laplace",laplace);

waitKey(0);
return0;
}

除此之外，還有一些其他的拉普拉斯核：

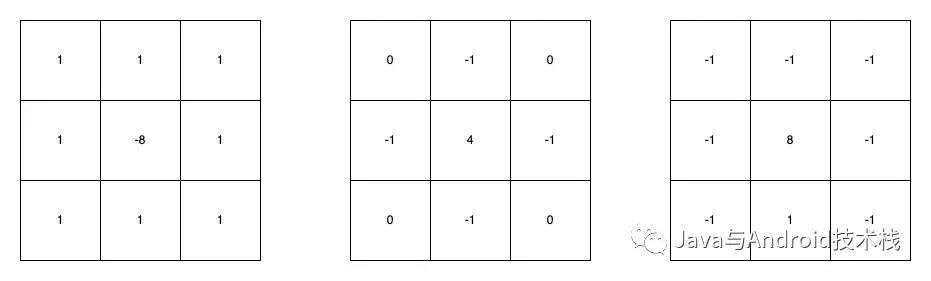其他的拉普拉斯核.png

后續(xù)的文章會詳細(xì)介紹拉普拉斯相關(guān)的內(nèi)容，以及如何在 OpenCV 中如何使用相關(guān)的函數(shù)，它的主要用途包括：

圖像銳化

邊緣檢測

模糊檢測

32.3 圖像的梯度及其性質(zhì)

梯度是一個有大小有方向的向量。梯度的方向是函數(shù)變化最快的方向。

圖像梯度是指圖像某個像素在 x 和 y 兩個方向上的變化率(與相鄰像素比較)，它是一個二維向量，由 X 軸的變化、Y 軸的變化這2個分量組成。

向量的幅度(長度)

幅度由 M(x,y) 表示，根據(jù)歐幾里得范數(shù)(L2 范數(shù))可得：

其中， M(x,y) 是與原圖像大小相同的圖像，它是 x 和 y 在 f 的所有像素位置上變化時產(chǎn)生的，也被稱為梯度圖像。

求梯度的幅度時，由于公式(8)的計算量比較大，可以用 L1 范數(shù)來近似梯度的幅度：

梯度的方向角

經(jīng)典的圖像梯度算法是考慮圖像的每個像素的某個鄰域內(nèi)的灰度變化，利用邊緣臨近的一階或二階導(dǎo)數(shù)變化規(guī)律，對原始圖像中像素某個鄰域設(shè)置梯度算子(例如 Sobel 算子、Roberts 算子、Robinson 算子、Laplace 算子等等)，通過圖像卷積實(shí)現(xiàn)對圖像兩個方向上梯度的計算。

Part33. 總結(jié)

本文介紹了圖像邊緣的含義，通過圖像邊緣引出圖像的梯度的概念。用數(shù)學(xué)的方式推導(dǎo)出圖像梯度并介紹了其相關(guān)的性質(zhì)。梯度是一個基礎(chǔ)且重要的概念，遍布機(jī)器學(xué)習(xí)、深度學(xué)習(xí)的領(lǐng)域。

介紹它們是為了后續(xù)介紹各種圖像邊緣檢測算法做準(zhǔn)備的，畢竟邊緣檢測是傳統(tǒng)的圖像分割算法。

審核編輯：湯梓紅