在《IGBT的物理結構模型》中，我們將IGBT內部PIN結切分成了PIN1和PIN2（見上一節插圖）， 因為PIN1與溝槽所構成的MOS串聯，而IGBT關斷是通過MOS溝道夾斷而關斷，而分析PIN1時所采用的邊界條件為陰極只有電子電流，空穴電流為0，因此PIN1部分的電流隨著MOS關斷會迅速降低到0，對后續關斷瞬態的分析影響很小。

而PIN2部分的電流則會通過復合緩慢衰減，是后續關斷中電流的主要構成部分，因此這里我們只討論PIN2的穩態和瞬態過程。

在之前的分析中，我們采用了對稱的一維坐標體系，即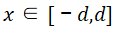，對穩態的載流子濃度分布進行推導。考慮到關斷瞬態過程中，耗盡區會逐漸擴大，基于該坐標體系的部分會逐漸減小，即非耗盡區逐漸減小，不再相對中點對稱，顯然對稱坐標體系不便于后續的梳理推導。這里我們先更換坐標體系為，其中為非耗盡區寬度，重新求解擴散方程(6-2)，并將結果作為后續關斷瞬態的初始條件。

如圖所示，假設IGBT基區寬度為，回顧《IGBT中的若干PN結》中關于反偏PN結的耗盡區寬度計算，顯然，

其中，為base區摻雜濃度， 為BJT基極與集電極之間的反偏電壓。需要注意的是該等式中忽略了內建電勢以及p-base的濃度影響。在導通狀況下， 近似認為0，但關斷過程中，主要依靠所在位置的反偏PN結承受電壓，近似認為等于外界施加電壓。

回顧《IGBT的物理結構模型》的PIN結構模型，取陽極邊界條件（IGBT集電極）為電子電流，在這里即，其中表示總電流。為簡化運算，直接令（稍后我們會給出與之間的關系），這樣邊界條件根據坐標系的變更調整如下：

（6-2）的通解是 ，根據邊界條件（6-8），很容易計算出通解的系數和分別為：

將系數和分別帶入的通解表達式，并利用，可以得出穩態下的表達式：

下面我們看看與電流之間的關系。在處，將（6-10）求微分，然后將結果帶入邊界條件，得到：

所以，當通過IGBT的總電流確定后，通過(6-10)和(6-11)即可計算出IGBT內部任意位置的多余載流子分布。

需要注意的是，上述分析均是基于大注入的模型假設，即任意位置均成立，但是顯然在接近BJT集電極的位置，因為PN結反偏， ，所以大注入條件在這個位置是不成立的。

盡管如此，這個區域占比很小，因此大注入模型依然能夠比較準確地分析和電流分布的影響。

后面，基于穩態的分布，我們將逐一構建起電流（包括電子電流和空穴電流）、電壓與之間的關系，再通過與或者之間的關系，并將其作為后續關斷瞬態分析的邊界條件。

圖中繪出了隨總電流的變化趨勢， 橫坐標處的載流子濃度即為，顯然隨增大而增大。（6-11）所給出的與的關系是基于PIN結構模型。但實際上基于BJT模型，存在基極的電子電流，這部分電流電流必須要經過BJT發射極（IGBT集電極）流出，所以。下面我們會再基于BJT結構模型來進一步修正、與的關系。