對于信號而言，phase shift是一個相對值，而time delay是絕對值。有時候我們關(guān)心time delay，那么如何由phase得到延遲時間呢？

假設(shè)信號經(jīng)過一階低通濾波器（-3dB帶寬為f0），那在所有頻率點(diǎn)，信號的delay是怎樣的？

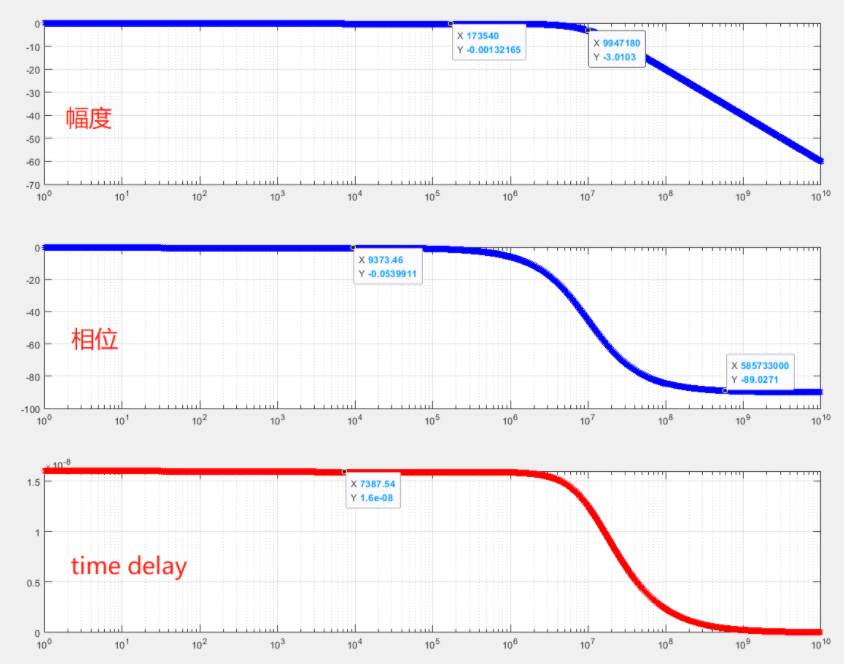
tao=16ns時，我用matlab plot了一下幅度、相位和time delay，其中**time delay=phase/w ** (其中w為角頻率，phase量綱為rad/s)

可以看出低頻的time delay=tao，高頻信號沒有delay。

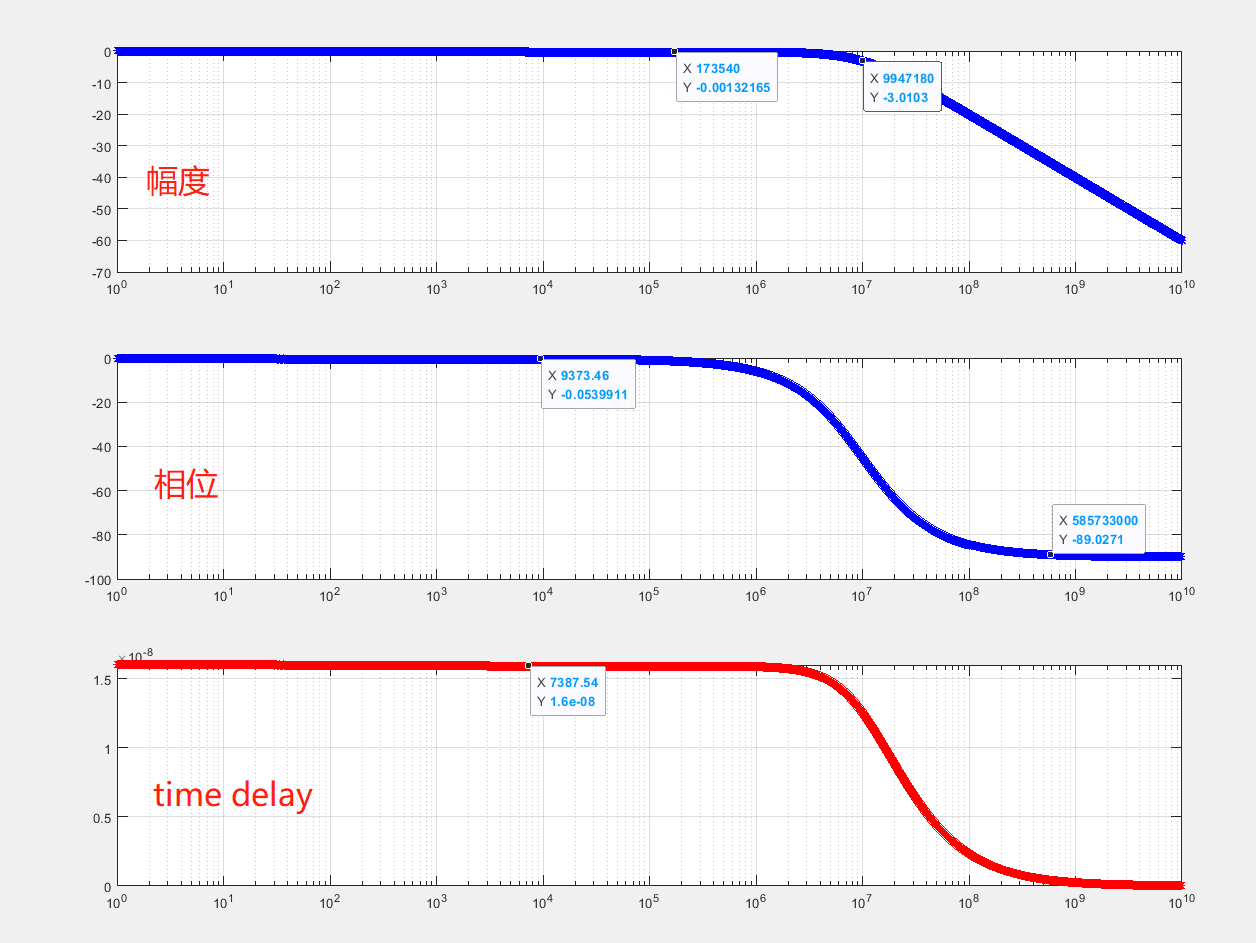
在數(shù)學(xué)上time delay=arctan（f/f0）/(2pif)

當(dāng)f/f0為無窮小時，上式近似為1/(2pif0)=tao ==>原來tao的物理意義在這里，意味著小于f0的頻率基本都delay tao。

當(dāng)f遠(yuǎn)大于f0時，time delay=0，可以理解為相位偏差90度但由于周期無窮小，所以delay為0；

中間階段就按照arctan（f/f0）/(2pif)的公式來，time delay和頻率是一個非線性的關(guān)系。

我因此繼續(xù)延伸一個話題：一個閉環(huán)運(yùn)放，當(dāng)gbw不變，而phase margion變化時，在gbw處的環(huán)內(nèi)信號（也可以理解為干擾） delay time一樣嗎？如果環(huán)內(nèi)信號的delay time特別關(guān)鍵，那么可以認(rèn)為即使gbw相同，當(dāng)phase margion不同時，在gbw處的干擾信號的抵消速度不一樣。

再進(jìn)一步，如果是一個dc-dc或pll，帶內(nèi)雙極點(diǎn)，一個零點(diǎn)，那么即使gbw不同，在零極點(diǎn)位置相同（dc增益不同）時，環(huán)路的響應(yīng)速度（高頻處的相位）是一樣的（但抵消的幅度不一樣，這么分析好像實(shí)際意義不大，但把環(huán)路反饋拆分為速度（時間）和幅度，有利于更細(xì)致的分析環(huán)路響應(yīng)問題和做改進(jìn)）。

再往前，環(huán)路問題拆分為幅度和速度（時間，也可以認(rèn)為是頻率）后，在sdm adc中，如果要優(yōu)化int1對idac的瞬態(tài)響應(yīng)，由于idac方波中包含了各種頻率分量，為了使方波中各次諧波都能有響應(yīng)，此時opamp的gbw要足夠大。

而當(dāng)設(shè)計(jì)一個濾波器，想要在某個頻段有很好的線性度時，可以不用做很高的gbw，而利用一些復(fù)極點(diǎn)把關(guān)心的頻段做一個peak即可。

以上的分析說明，明確對速度（頻率）和幅度的要求后，改進(jìn)方法會很有針對性。