前兩篇中，我們介紹了諧振電路系統(tǒng)的時域分析方法和頻域分析方法，并結合了不同的電路實例，總結了軟開關ZVS的實現(xiàn)條件。我們的思路是從最基本的電力電子電路出發(fā)，逐步將諧振和軟開關的概念引入到PWM電力電子電路中，所以我們重點關心了電路的模態(tài)和波形等時域表現(xiàn)。我們從直觀上對時域的模型更熟悉，但從電路分析的角度，模態(tài)和波形分析只是在某一個具體的頻率條件下進行的。

對于諧振電路而言，如果只了解電路的時域表現(xiàn)，就仿佛是只看到了冰山一角 ，和頻率相關的大部分知識都藏在海底。而今天我們需要做的，就是要讓剩下的冰山，全部浮出水面。

一.再論歐姆定律

大家可能覺得很奇怪，歐姆定律這種初中生就知道的常識，為什么還要拿來這里說。這里，我們討論的歐姆定律，不再從時間的角度考慮，而是從頻率的角度考慮，它描述的是電壓和電流的一種線性關系。比如，在直流穩(wěn)態(tài)電路中，我們知道，要計算某段導體的電阻，只需要用這段導體兩端的電壓除以流經導體的電流即可得到。

那么，當我們在這段導體上施加的電壓是交流電壓，而且電壓是以正弦波的形式交變，我們還能得到相同的結論的嗎？如果把這段導體認為是理想的純電阻，答案是肯定的。施加頻率為f1的正弦波電壓，就得到頻率為f1的正弦波電流；施加頻率為f2的余弦波電壓，就得到頻率為f2的余弦波電壓。在任何頻率下，電阻兩端的電壓都與流經電阻的電流成正比，這個比例系數(shù)，就是電阻值。

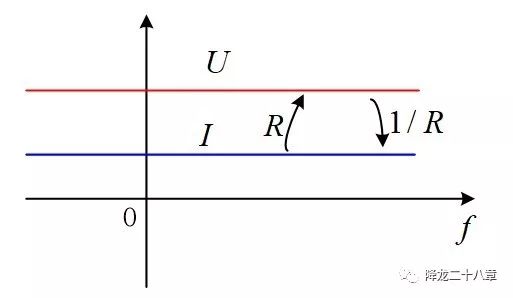
這樣，在整個頻域，電壓和電流形成了一種映射，而且是一種線性映射，這就是歐姆定律在頻域的本質。

但是實際上，任何導體都不可能是理想的純電阻。

當我們把兩端正弦波電壓頻率增高（比如到了100MHz），我們會發(fā)現(xiàn)流經導體的電流的相位和施加的電壓相位有些偏差，學過電路理論的人應該都知道這是由于導體的高頻感抗造成的。

在一些電工學的教材中，正弦穩(wěn)態(tài)分析和阻抗的概念被引入。把電壓和電流當做旋轉矢量這種方法，與我們第一篇提到的簡諧振動旋轉矢量類似。

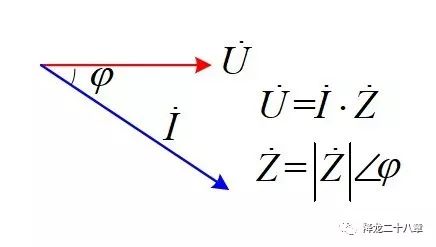
但穩(wěn)態(tài)意味著只在某個頻率點，我們之前提到，電力電子電路中存在大量的開關動態(tài)，一個開關（階躍）動作，就意味著無數(shù)多個高頻激勵分量。這樣，正弦穩(wěn)態(tài)分析的方法不再適用，我們需要找到更廣義的解法--頻域阻抗。

在頻域中，我們假定存在這樣一個激勵：激勵電流Iin(f)=1，即激勵電流由無窮多個頻率下的單位激勵合成，如果我們想要關心電路系統(tǒng)在任何頻率下的電壓響應，那我們就需要一個關于頻率f的阻抗函數(shù)，這個阻抗函數(shù)不僅要包含在各個激勵頻率下的電壓電流幅值的比例系數(shù)信息，還要包含了各個頻率下電壓電流的相位差信息。

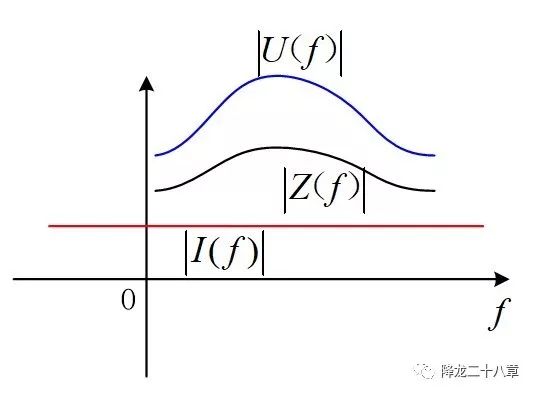
因此，我們需要引入頻域阻抗（或者復阻抗）的概念。如果說正弦穩(wěn)態(tài)分析中的阻抗是海面上我們看得到的冰山，那整個頻域的頻域阻抗就是包含了海底部分的整個冰山。

頻域中，電感的阻抗和頻率成正比，這是由電感的充放電關系決定的

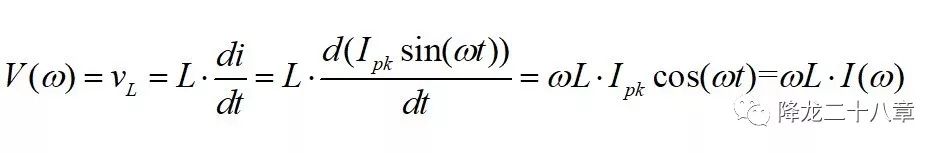
電容的阻抗和頻率成反比，這是由電容的充放電關系決定的。

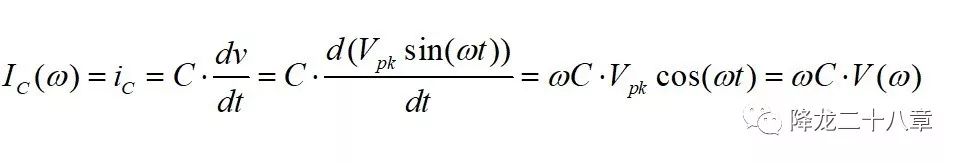
我們知道，諧振網絡主要是由電感、電容和電阻三種元器件組成，這樣我們可以把諧振網絡等效成一個線性二端口網絡。

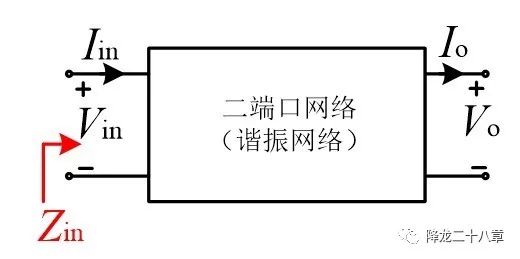
二端口網絡的左側認為是輸入側，一般接能量供給單元，例如電壓源，電流源等，右側認為是輸出側，一般接能量消耗單元，例如電阻（或者等效的電壓源，電流源）。當負載接入后，從左側看過去，可以認為輸入電流和輸入電壓滿足一定的函數(shù)關系：

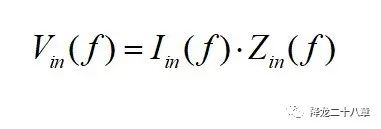
這里的Zin(f)即為這個二端口網絡等效的輸入阻抗。它反映了特定負載條件下，施加不同頻率的激勵（可以是電壓，也可以是電流），二端口網絡從輸入端表現(xiàn)出來的外特性。

怎樣量化這個阻抗呢？

從電路的頻域模型入手。

比如一個簡單的LCR網絡，容易得到其頻域模型，令初始狀態(tài)為零，可以得到從輸入電流到輸入電壓的傳遞函數(shù)。只需要將傳遞函數(shù)中的s，代換成2πjf,這里的f是頻率，j是單位虛數(shù)。

這樣根據頻域模型得到的傳遞函數(shù)便有了物理意義，它表示系統(tǒng)在各個頻率點的輸入阻抗Zin(f）。各個頻率的輸入阻抗Zin(f)都是復數(shù)，它的幅值規(guī)定了輸入電壓幅值和輸入電流幅值的比例，幅角定義了該頻率下輸入電壓超前于電流的相位角。

二.正弦波等效分析

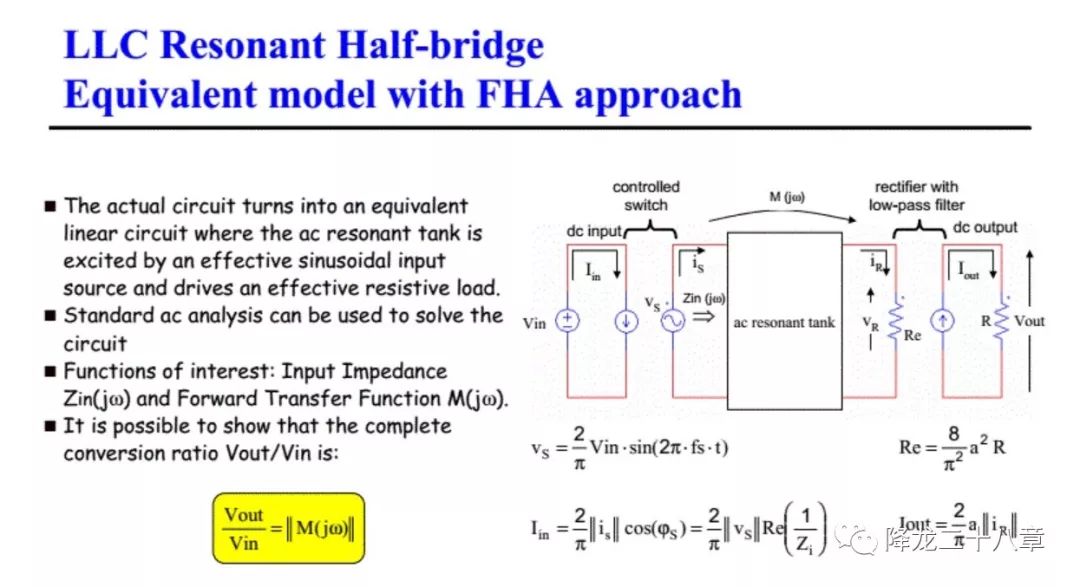
前文中我們講到了諧振網絡的輸入阻抗概念，接下來我們便要將這個概念應用到諧振變換器中。以串聯(lián)諧振DC/DC變換器為例，下圖是該變換器的電路拓撲。

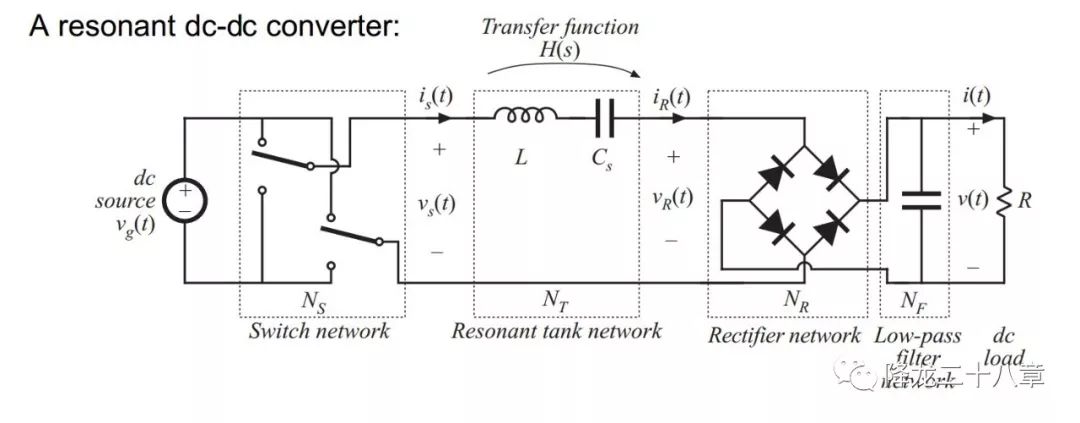
這是一種典型的諧振變換器電路，電路由四個二端口網絡構成，開關網絡，諧振網絡（或者稱諧振腔），整流網絡，濾波網絡。

從傳遞函數(shù)的角度來看，開關網絡和整流網絡都是含有開關器件的非線性網絡，而諧振網絡和濾波網絡則是線性網絡。我們的目的是要從頻域分析整個電路的特性，所以對各個網絡做單獨的等效處理，將所有的非線性網絡等效成線性網絡。

首先關注開關網絡。由于輸入電壓源的存在，開關網絡的輸出電壓為方波電壓。同時諧振系統(tǒng)具有選頻特性，可認為諧振腔只對諧振頻率的激勵進行響應。 所以我們不妨假設開關網絡的開關頻率接近諧振頻率 ，這樣開關網絡的方波輸出電壓中只有其基波分量被響應，其他頻次分量都可忽略。

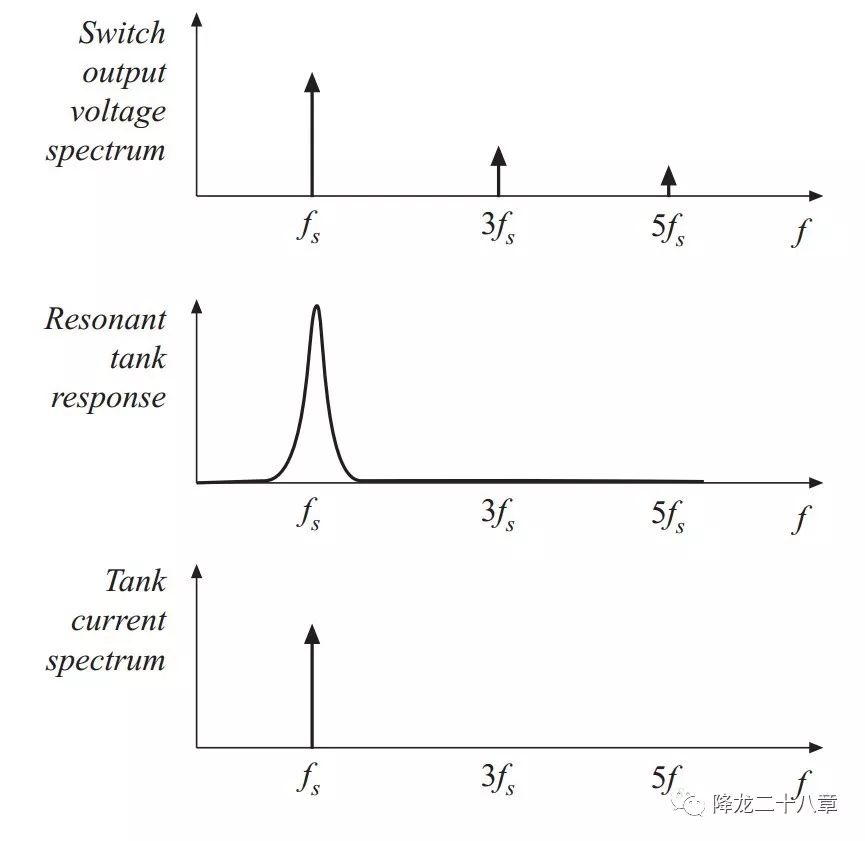
開關網絡的輸出方波電壓做傅里葉分解后的基波電壓如下

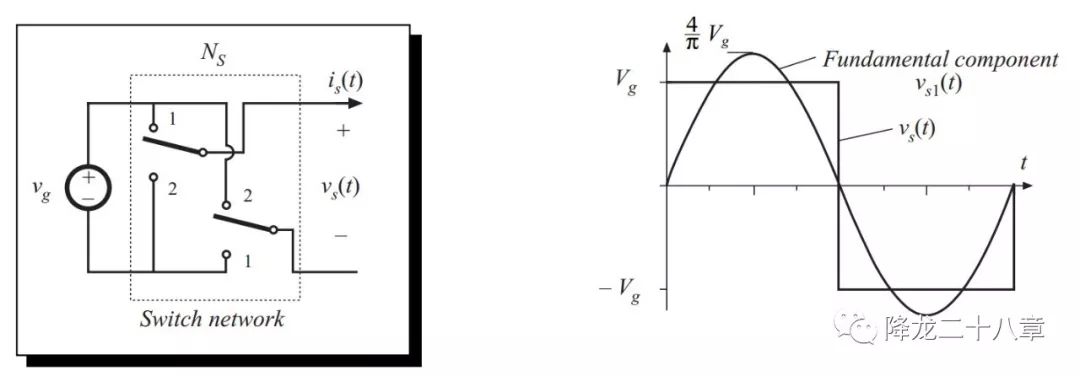
開關網絡的輸入電流波形如下

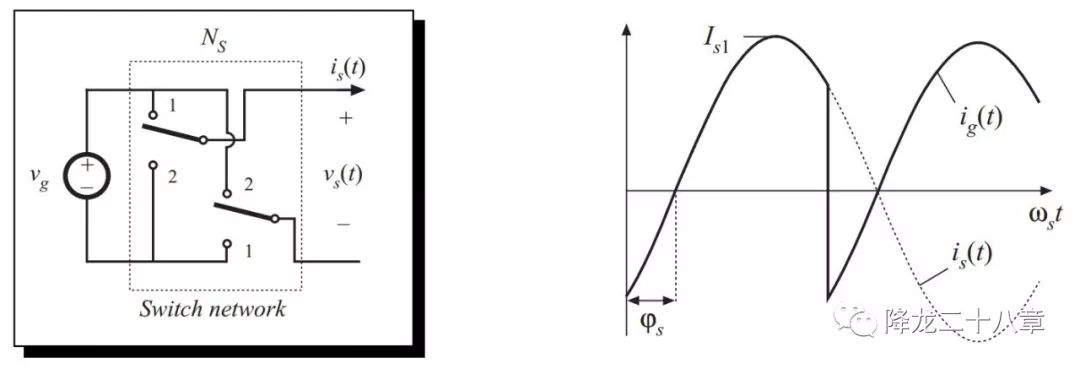
其中，ψs為諧振腔的響應電流（同時也是開關網絡的輸出電流）滯后于開關網絡輸出電壓基波的相角，Is1為響應電流的幅值。

可以對開關網絡輸入電流求取一個周期內的直流分量

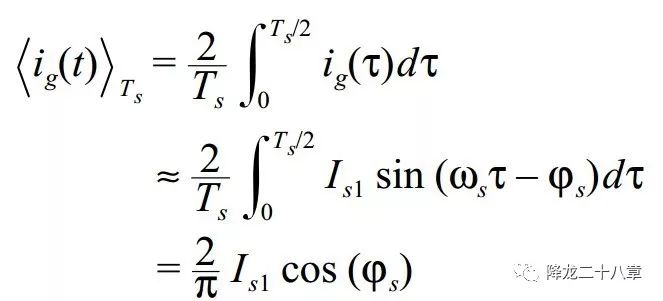
這樣，我們可以把電源及開關網絡等效成如下形式

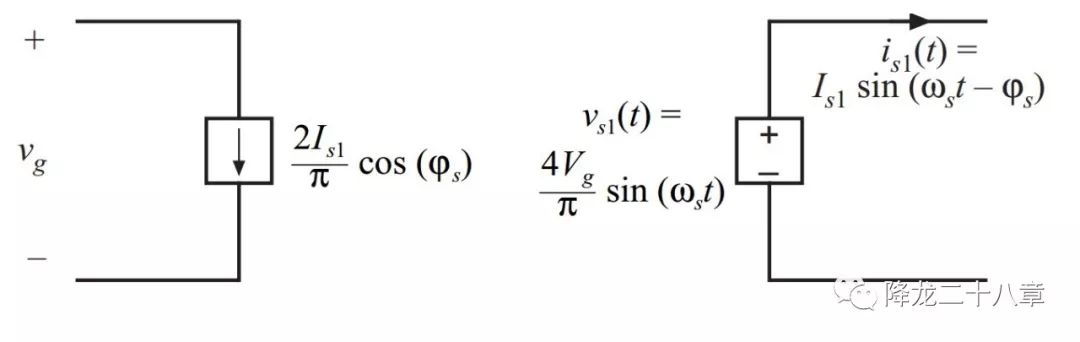
左邊代表直流電源輸出直流電，直流電負載即為開關網絡輸入電流的平均值。右邊代表交流電壓源給諧振網絡輸出交流電，交流電壓源的幅值為開關網絡輸出方波電壓的基波幅值，交流電頻率為開關頻率。

同樣的方法，我們可以對整流網絡和濾波網絡等效，由于容性負載的存在，整流網絡的輸入電壓為方波電壓（V為輸出直流電壓）

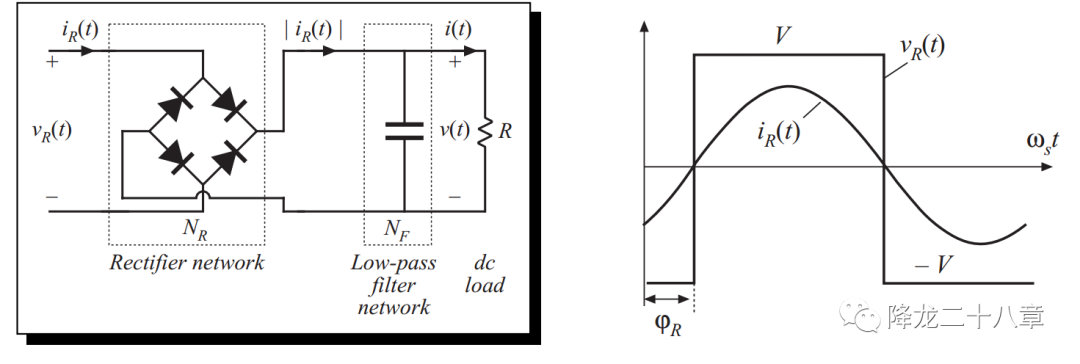
對整流網絡的輸出方波進行傅里葉分解，

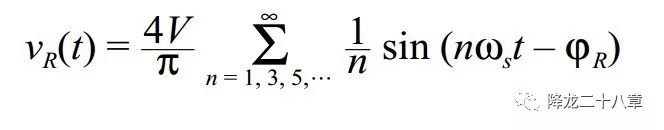
整流網絡的輸入電流為諧振網絡的輸出電流，（這里我們考慮的是LC串聯(lián)諧振網絡，諧振網絡的輸出電流與輸入電流相等,is1=ir1,ψs=ψr,，如果是其他形式的諧振網絡，則輸入輸出電流未必相等）：

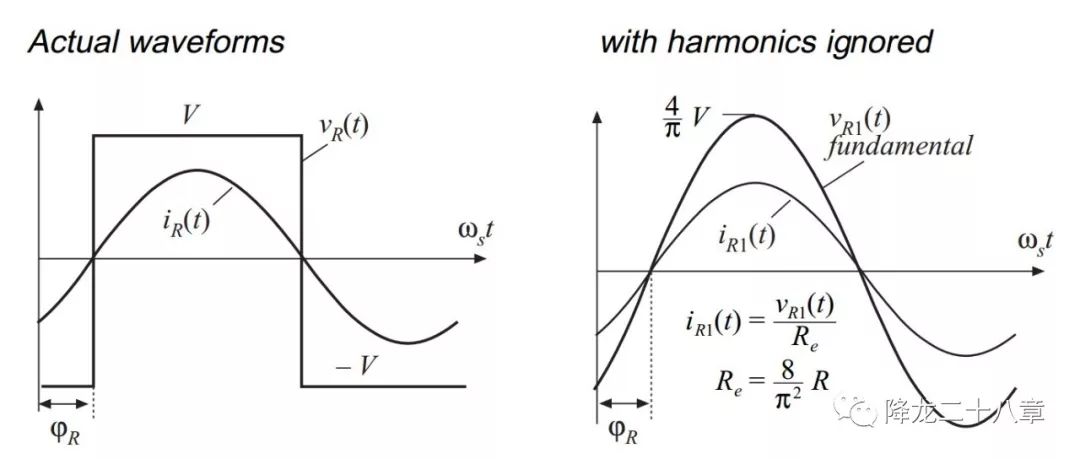
考慮整流網絡的輸入電壓基波幅值與輸入電流的幅值比例及相位關系，可以得到的整流網絡及濾波網絡（負載電阻為R）的等效輸入阻抗，這個阻抗是一個純電阻，可以表示為Re。

這樣就可以得到由整流網絡，濾波網絡及負載電阻構成的等效電路如下圖

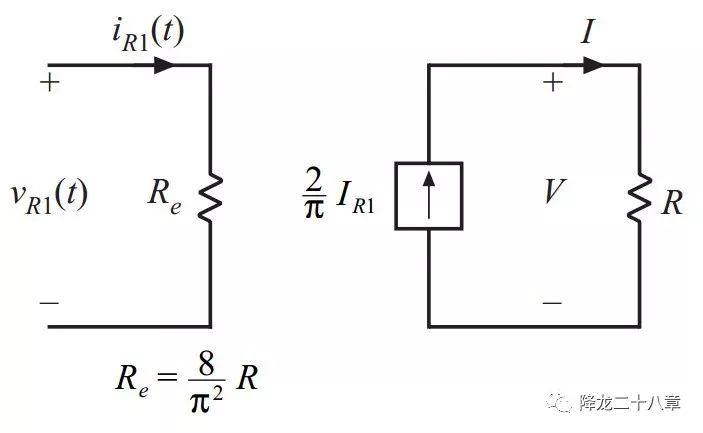
接下來，我們便可以對整個諧振變換器電路進行等效，非線性網絡被等效成了線性網絡。

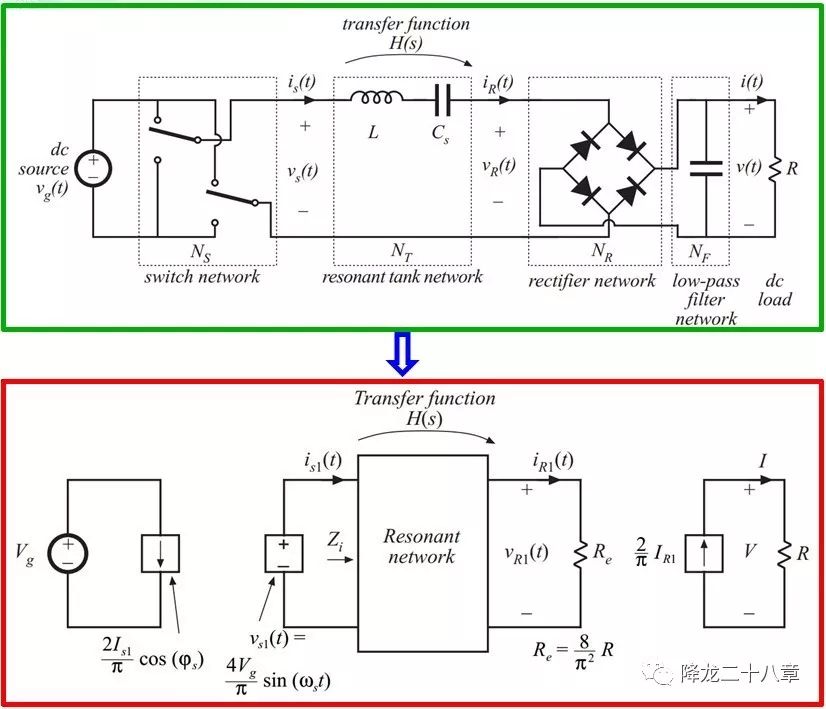
我們只需要關心等效后的諧振網絡部分的頻域特性，問題被大大簡化。 這樣的分析方法，被稱為基波等效分析法 。這樣，所有針對諧振變換器的分析工作，都可以圍繞諧振網絡的特性展開。

那么我們需要關心諧振網絡的哪些特性呢？

1. 阻抗特性。分為輸入阻抗和輸出阻抗，輸入阻抗的幅值決定了輸入電流對輸入電壓的響應比例，這對于開關管的電流應力是決定性因素；輸入阻抗的相角是實現(xiàn)開關管軟開關的關鍵因素；對于輸出阻抗，則決定了系統(tǒng)的阻抗匹配，當系統(tǒng)輸出阻抗成純阻性時，這時調節(jié)負載等效電阻Re，使其等于輸出阻抗，Re變能獲得最大的輸出功率。
2. 增益特性。這個諧振變換器例子中的輸出為電壓源型負載，穩(wěn)態(tài)的輸出電壓V與輸入電壓Vg的比例是這個電路的增益M，這個增益顯然和諧振網絡的輸入輸出電壓傳遞函數(shù)H(s)有關。

以串聯(lián)諧振變換器為例，輸入輸出電壓增益M等于諧振網絡輸入輸出電壓傳遞函數(shù)H(s)的幅值（證明如下圖），

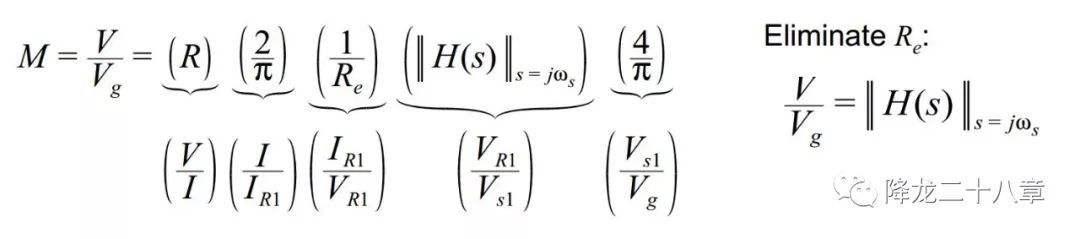
下圖為串聯(lián)諧振變換器的諧振網絡輸入輸出電壓傳遞函數(shù)。

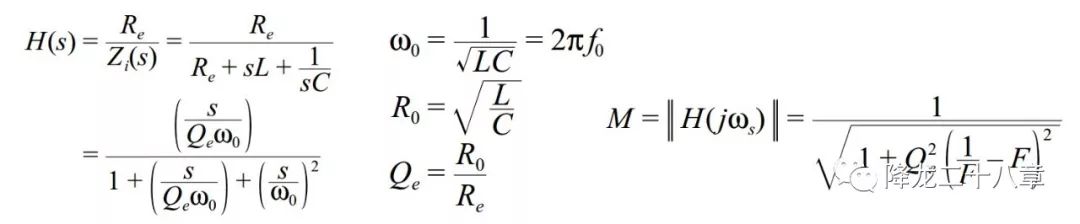
除了公式表示以外，還可以通過曲線圖表示增益特性和阻抗特性

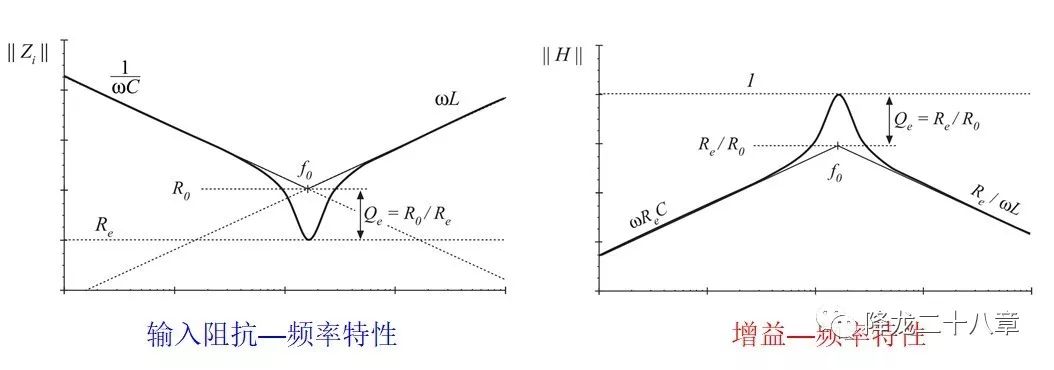
以上兩點就是阻抗特性和增益特性分析諧振變換器的 兩大利器 。可以看到，這兩個特性都是和開關頻率相關的，可以寫成開關頻率的函數(shù)，這就是典型的頻域分析。

值得注意的是，傳遞函數(shù)這種頻域函數(shù)只有在把自變量s換成了2πjf時才具有明確的物理意義。并且，傳遞函數(shù)是基于零初始狀態(tài)的條件得到的，當系統(tǒng)的初始條件不可忽略時，傳遞函數(shù)的方法便不再適用，這時再采用時域微分方程結合電路模態(tài)分析是一種解法，但更多的時候，使用狀態(tài)空間的方法會更簡潔，有興趣的讀者可以參考現(xiàn)代控制理論的相關內容，這里不再贅述。

三.LLC電路實例

前文中，我們以串聯(lián)諧振變換器為例，給出了諧振變換器的頻域分析方法--基波等效分析法。這部分內容都是在從數(shù)學的角度建立模型，說白了就是空洞洞的理論。現(xiàn)在，我們便將這一理論應用到一個非常典型的實際變換器中，畢竟，實踐是檢驗理論的唯一標準嘛。

提起LLC諧振變換器，相信大家都有所了解。業(yè)內有非常多的產品和研究工作就是基于LLC諧振變換器的，所以今天我們不再對它的電路模態(tài)這些細節(jié)做詳細的介紹了。

我們把前文提到的兩大利器應用到這個電路里面，讓大家理解這個變換器最基本的道理就Ok。

如果看官們對LLC變換器的相關知識感興趣，我給各位推薦兩份資料，第一份是意法半導體（ST）制作的LLC分析文檔，在百度文庫上可以查到；第二份是一篇博士論文，題為Investigation of High-density Integrated Solution for AC/DC Conversion of a Distributed Power System。

首先，我們來看全橋LLC諧振DC/DC變換器的電路拓撲結構

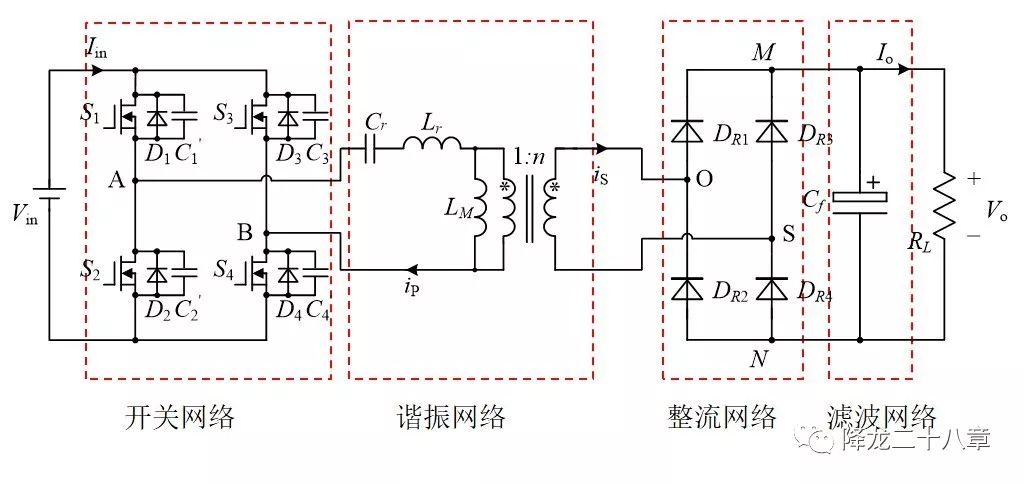
可以看到，這個變換器的結構與前文中的串聯(lián)諧振變換器一樣，可以分為開關網絡，諧振網絡，整流網絡和濾波網絡四個二端口網絡。不同的是，這個電路拓撲的諧振網絡是一個帶變壓器的二端口網絡，并且有三個諧振元件，諧振電感，諧振電容，變壓器勵磁電感。

由于結構與上文分析的一致性，我們可以把上文中的分析方法應用到這個LLC拓撲中，同樣關注諧振網絡的頻域特性。

和上一篇一樣，我們再看看LLC諧振變換器的ZVS條件。

我們知道，諧振網絡的輸入電壓基波與輸入電流存在相位角，這個相位角就是輸入阻抗在基波頻率點的相位角。

那么這個相位角對于開關網絡意味著什么呢？

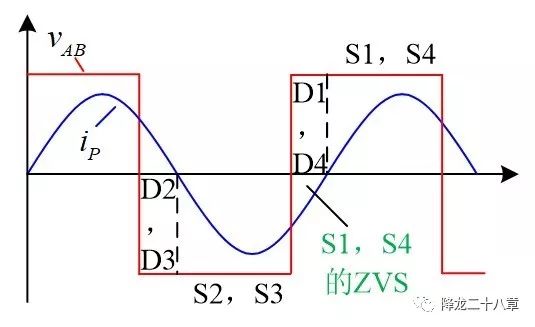
如下圖，紅色為方波輸入電壓，藍色為原邊的諧振電流，圖中表現(xiàn)的是電流相位滯后于電壓相位的情形。當VAB為負向輸入電壓時，表示2，3管導通，要么是2，3管的溝道導通電流，要么是2，3管的寄生二極管導通，可根據電流方向區(qū)分。當2,3管同時關斷后，考慮死區(qū)時間，1，2，3，4管都是處于關斷狀態(tài)。如果此時的諧振電流為負值，便會給2，3管結電容充電，給1，4管結電容放電，如果能量足以將1，4管結電容電壓降至零，再經1，4管的寄生二極管續(xù)流，便具備了實現(xiàn)軟開關ZVS的條件。

接下來是電流超前于電壓的情況。如下圖，在VAB為負輸入電壓時，2，3管先由溝道導通負向電流，再由寄生二極管導通正向電流。電流從溝道換向二極管的過程，電流從峰值降到零，再變?yōu)樨撓颍且粋€自然換流的過程，此時即使S2,S3的驅動為高，電流也不再通過溝道流通。二極管續(xù)流一段時間后，S2，S3驅動變低，關斷S2,S3，這就實現(xiàn)了S2,S3管的ZCS。關斷S2,S3后，經過短暫的死區(qū)時間后再開通S1,S4。S1,S4開通時，二極管S2,S3還流通正向電流，但其電壓迅速上升至輸入電壓，強制S2,S3關斷，這時D2,D3會產生嚴重的二極管反向恢復問題，而此時S1,S4已開通，相當于橋臂形成直通，如果能量足夠大，就有損壞器件的風險。另外，反向恢復過程還伴隨較嚴重的電壓震蕩問題，不僅增加了損耗，而且可能超過器件的安全工作區(qū)導致失效。 所以ZCS的情況需要盡量避免。 這部分內容在我推薦的第一份資料里有詳細的介紹，大家可以參考。

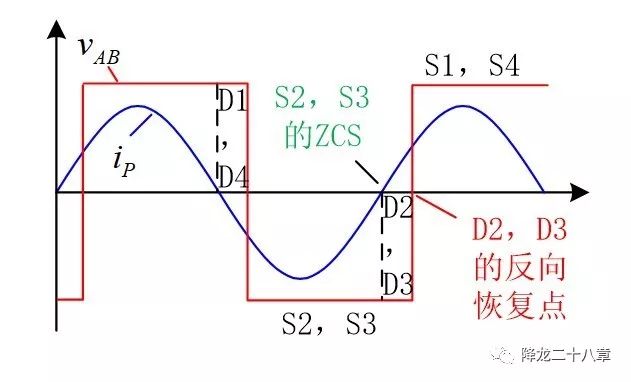
一般的LLC諧振變換器設計，會規(guī)定感性區(qū)和容性區(qū)，就是從輸入阻抗的角度考慮的，因為感性區(qū)意味著電流相位滯后于電壓相位，可以實現(xiàn)ZVS。而容性區(qū)則意味著電流相位超前于電壓相位，是ZCS區(qū)，需要避免。

上文中我們討論了輸入阻抗特性對于開關網絡ZVS的實現(xiàn)的作用，下面我們討論增益特性對系統(tǒng)的影響。

下圖是LLC變換器的歸一化增益曲線，所謂歸一化，就是將橫坐標的開關頻率fs換成了開關頻率與諧振頻率的比值fn。另外，我們把勵磁電感Lm與諧振電感Lr的比例記為k，諧振網絡特征阻抗與等效電阻Re的比值記為Q，可以得到增益函數(shù)是關于fn,k,Q的函數(shù)M（fn,k,Q)

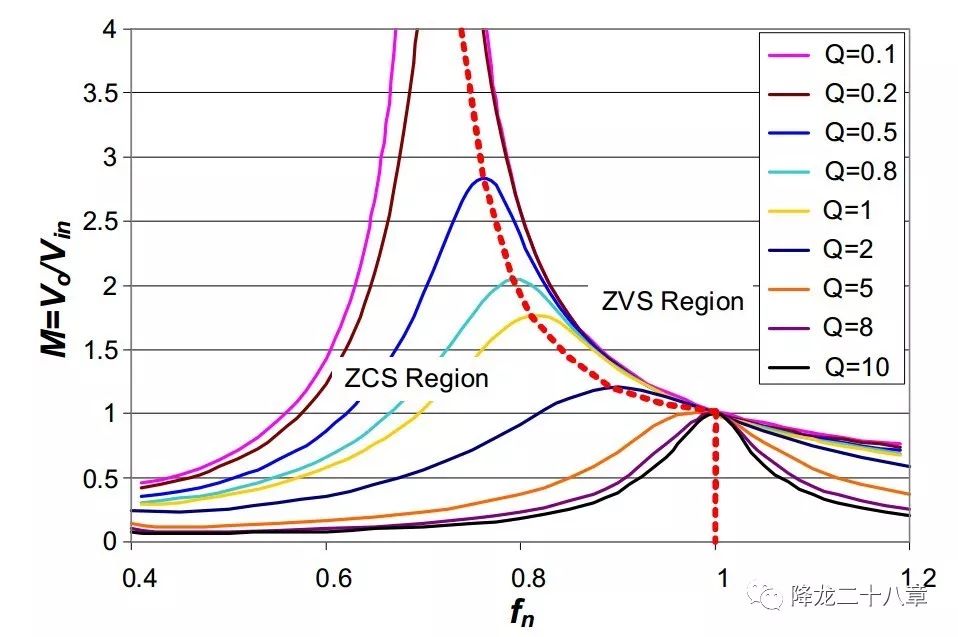
圖中紅色虛線為輸入阻抗的純阻性曲線，曲線的右邊意味著感性區(qū)和ZVS，右邊意味著容性區(qū)和ZCS。

值得注意的是，這個曲線是在某個特定的k下得到的，也就是說，改變勵磁電感與諧振電感的比例，增益曲線的形狀也會變化。

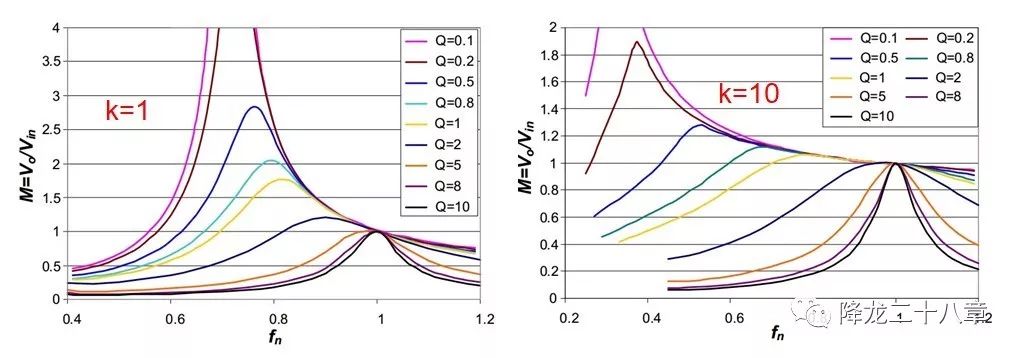
從圖中可以看到，當k值變大后，增益曲線變“平坦”，這意味著要獲得相同的增益變化范圍，k值大的諧振網絡需要的頻率變化范圍比k值小的諧振網絡需要的頻率變化范圍更大。這即是我們所說到的敏感性，LLC諧振變換器的增益對開關頻率的敏感性是和k值相關的。

在一些恒流輸出場合，比如3.3kW的恒流輸出的車載充電器，經過PFC整流后的母線電壓是380V-420V直流，要通過LLC諧振變換器轉化成70V-120V/30A的直流電壓電流給電池供電，再比如中大功率恒流型LED驅動電源，同樣PFC后的直流母線電壓需要轉化成20-48V的直流電壓。這些場合輸出電壓變化范圍寬，需要的電路增益變化范圍較大，而控制器的開關頻率變化范圍是有限的。這時可以使用k值較低的諧振網絡，使得開關頻率的變化范圍在控制器的輸出能力之內。

但如果k值過小，會有什么問題？

k值較小，意味著勵磁電感相對于諧振電感較小，勵磁電流相對于諧振電流不可忽略。變換器進入輕載時，勵磁電流帶來的磁芯損耗較大。另外，原邊電流中激磁電流的成分多，同時也增加了高頻線損。下圖為勵磁電感較小（k=2)的一個例子，紅色為橋臂中點電壓VAB，黃色為原邊電流ip。

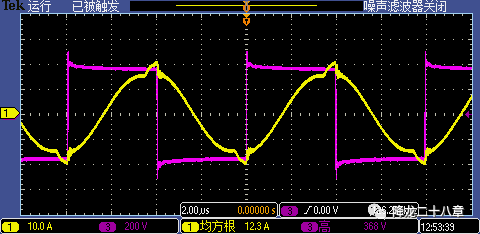
事實上，當我們規(guī)定了電路需要的最低增益，諧振頻率和允許的最高開關頻率后，我們可以定量地計算得到k值，具體參考ST的LLC文檔。但在電路調試的過程中也會看到k值的影響，不止是在損耗和效率方面，k值對控制電路，電壓應力等都是非常重要的。我們往往會對k值有一個預期，根據工程師經驗，可以大概給出一個特定場合應用的k值范圍。至于合不合理，就要看工程師的道行了。感興趣的讀者可以繼續(xù)深入地分析k值對電路方方面面的影響。

對于LLC的具體設計，我提到的兩篇文檔中都有足夠詳細的內容，所以我不再多說。文檔中提到的都是恒壓輸出的應用場合，感興趣的讀者可以思考恒流輸出應用場合的設計有何異同。我們只提示大家一個方法，就是 尋找設計的邊界條件 ，比如增益邊界，最高開關頻率，最大功率范圍（空載到滿載），ZVS實現(xiàn)條件。 如果弄清楚了各個邊界與我們提到的Q值，k值等頻域參數(shù)的關系，設計就迎刃而解了 。

總結

以上，我們把頻域的分析方法應用到了串聯(lián)諧振拓撲和常用的LLC拓撲中，重點關注了基波分析法的由來和阻抗特性，增益特性在變換器中的體現(xiàn)，希望大家看了之后看清諧振變換器的本質，不再被這些復雜的公式和流程嚇倒。