在之前的筆記中我簡要記錄了pipelined ADC中的數字校準技術,也就是消除子ADC失調的方法,但記錄的并不全面,理解的也不夠透徹,這里重新系統地再解釋一下其原理及由來。
本文主要參考了Imran Ahmed的”Pipelined ADC Design and Enhancement Techniques”一書
Imran Ahmed的書中提供了一個很好的角度來理解流水線ADC的工作原理,我們可以使用除法來進行類比,回憶我們計算十進制除法時的過程,首先,將被除數與除數進行比較,找到一個數使得其與除數的乘積最接近而不超過被除數,將其作為最高位的商,之后將被除數減去除數和此位商的乘積,得到的結果乘以10,繼續重復上述步驟。
根據以上的描述結果可以很清晰地看到,除法中每位商的計算過程與1bit的流水線子級的運算過程非常相似,被除數是要量化的模擬量,除數是LSB,商就是轉化結果,10就是級間增益,每次新得到的被除數就是殘差。
那么繼續思考這個過程,如果某一位商的運算結果錯了怎么辦,注意這個情況就對應于pipelined ADC某個子級中比較器的判決電壓產生偏移導致了誤碼,舉個例子,50/7,正常情況下的計算流程如下
| 位數 | 當前位商(當前子級的輸出) | 當前位商*除數(子DAC轉換結果) | 余數(殘差) | 新的被除數(放大到滿量程的殘差) |
| 1 | 7 | 49 | 1 | 10 |
| 2 | 1 | 7 | 3 | 30 |
| 3 | 4 | 28 | 2 | 20 |
| 4 | 2 | 14 | 6 | 60 |
| 5 | 8 | 56 | 4 | 40 |
| 6 | 5 | 35 | 5 | 50 |
根據上表,正常計算得到的結果為7.14285余5。
接下來假設第四位的商計算錯誤(對應于第四級流水線子級的比較器失調),將正確的2變為3,計算流程如下。
| 位數 | 當前位商(當前子級的輸出) | 當前位商*除數(子DAC轉換結果) | 余數(殘差) | 新的被除數(放大到滿量程的殘差) |
| 1 | 7 | 49 | 1 | 10 |
| 2 | 1 | 7 | 3 | 30 |
| 3 | 4 | 28 | 2 | 20 |
| 4 | 3 | 21 | -1 | -10 |
| 5 | -2 | -14 | 4 | 40 |
| 6 | 5 | 35 | 5 | 50 |
得到的結果為7.143(-2)5余5,很明顯,驗證后這個結果也是正確的。
那么就可以得到結論,即使某位發生了誤碼,只要將錯誤的結果完整地繼續傳遞下去,此運算結構依舊可以得到正確的結果。但是需要注意的是上述結論存在一個非常重要的前提,必須要將錯誤的結果完整地傳遞下去。
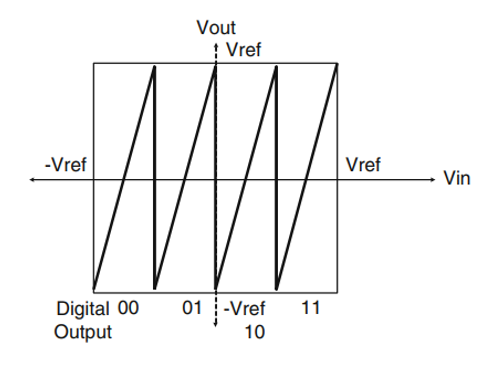
考慮一個兩位子級的傳輸特性曲線,如上圖所示,我們可以發現,輸出電壓最大值和最小值已經到達了Vref,一旦判決電壓發生偏移,如下圖所示,就會導致輸出超出下級的量程,換句話說,下一級并沒有足夠的位數來將超出量程的電壓記錄下來,那么之前得出的結論也就不再適用了。
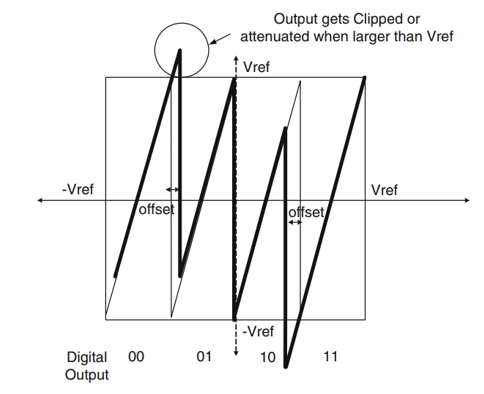
那么應該如何進行改進呢,很明顯,既然下一級的量程不夠,我們可以將當前級的級間增益縮小,如下圖所示,將級間增益由4縮小為2(注意這里實際上是將有效位減小為1位了),這樣一來,當前級的輸出就只有-Vref/2~ Vref/2的范圍了,而下一級的輸入范圍為-Vref~ Vref,正負兩端都留有Vref/2的余量,對應于比較器的判決電壓有Vref/4的偏移余量,換句話說,只要比較器判決電壓的偏移在正負Vref/4的范圍內,錯誤信息都可以完整地傳輸到下一級。
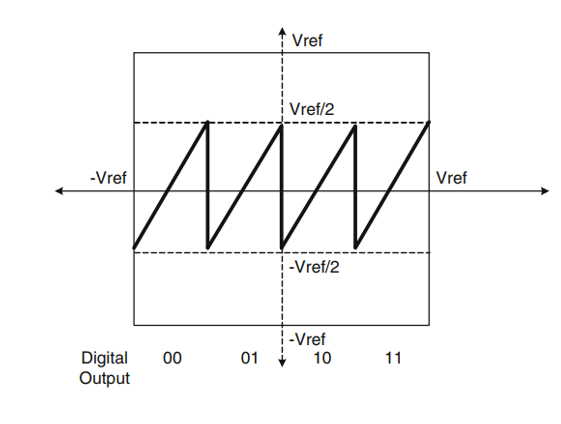
對于級間增益減半后的計算過程,從數字的角度來理解比較容易。舉個例子,假設理想的輸出數字量為4’b1011,轉換所用的ADC由一個級間增益減半的2-bit子級和一個3-bit Flash ADC構成,模擬輸入進第一級后輸出數字量為4’b10zz(這里用數碼z表示0的權重,注意這里數碼0的權重是負的),相減得到的殘差用數字量來表示為4’bzz11,由于級間增益減半,有效位只有一位,只需要左移一位得到4’bz11z,那么Flash ADC的轉換結果也就是3’bz11,等價轉化一下就是3’b101,將這個結果的最高位與2-bit子級的低位對齊進行錯位相加得到結果為4’b1011,正好為理想的輸出量。
觀察上述錯位相加的過程,由于數碼0的權重是負的,這就導致不能用簡單的二進制加法進行運算,注意到這里0+1=z,這相當于在數字邏輯中引入了減法運算,這是十分麻煩的,我們期望即便是在這樣的權重分配下依舊可以使用最簡單的二進制加法進行錯位相加。(Imran Ahmed的書中只是簡單提了一句,引文Chien, G.: High-speed, lower-power, low-voltage pipelined analog-to-digital converter. Masters of Science thesis, University of California Berkeley (1996),但我并未找到這篇文獻,有兄弟有資源的可以分享一下,以下都是我的個人理解)
那么應該如何實現呢,首先我們羅列出所有錯位相加的可能,如下表所示,假設有兩個級間增益減半的2-bit的子級級聯,其中第一行為第一級的輸出結果,第二行為第二級的輸出結果,結果1為直接使用普通二進制加法錯位相加得到的輸出,結果2位為正確的相加結果。
| 第一級 | 00 | 01 | 10 | 11 | ||||
| 第二級 | 01 | 10 | 01 | 10 | 01 | 10 | 01 | 10 |
| 結果1 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | 1000 |
| 結果2 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
可以明顯看出,結果1僅僅與結果2相差1,也就是說,如果將第二級的輸出結果減去1,那么直接采用普通二進制加法錯位相加得到的總的輸出結果就是正確的。舉個例子,第二級輸出為01,那么只要將01變為00即可,但這里需要注意,由1變到z對應于減Vref/8,而由1變到0對應于減Vref/4。
那么最簡單的方法,直接將轉移特性曲線向下平移Vref/2,也就是將輸出給下一級的殘差減小Vref/2(這是級間放大后的結果,從放大前角度看就是Vref/4),通過上述分析,這么做就可以直接對輸出進行錯位相加了。
然而新的問題又出現了,注意到直接將轉移特性曲線向下平移后輸出最小值又到達下限-Vref,這樣的一來比較器的判決電壓一旦發生負的偏移輸出又會超下一級的量程,我們之前將級間增益減半的做法又失去了作用。然而我們還可以發現,正的余量增加到了原來的2倍,既然如此,我們不妨將比較器所有閾值電壓都正向偏移Vref/4,這樣一來正負兩端的余量就又都是Vref/4了。最后得到的轉移特性曲線如下圖所示。注意這里閾值電壓的偏移不會引起任何輸出上的錯誤,就像之前說的,錯誤的量被完整地傳遞下去了。
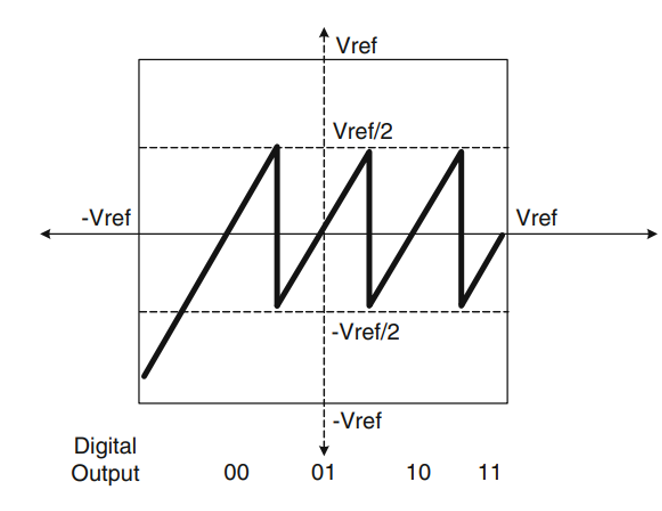
同樣,我們舉例具體描述一下轉換過程,假設理想結果為4’b1011,ADC由一個級間增益減半并將比較器閾值右移Vref/4的2-bit子級和一個3-bit Flash ADC構成,模擬輸入大小為Vref/2- Vref/4+ Vref/8+ Vref/16 = 7Vref/16,對應于區間10,輸出數字碼10,而由于閾值電壓右移Vref/4,子DAC輸出的模擬量為Vref/2- Vref/4+ Vref/4 = Vref/2,殘差為2*(7Vref/16 - Vref/2) = - Vref/8,同樣可以用數字量來表示,子DAC的輸出為4’b10zz + 4’bz1zz(加Vref/4) = 4’b1zzz,計算殘差,4’b1011 – 4’b1zzz = 4’bz011,左移一位得到4’b011z,經3-bit Flash ADC轉換出的結果為3’b011,直接使用普通二進制加法進行錯位相加,得到4’b1011。結果是正確的。
我們繼續觀察現在的傳輸特性曲線,注意到“11”這個區間實際上進行了一次多余的轉折判斷,實際上低位1的判斷完全可以交給下一級進行,縱軸上還存在Vref/2~Vref的余量,也就是說這個比較器的存在是可有可無的,那么再加入它就產生浪費了,因此我們將其移除。注意移除后正確性是可以保障的,因為當前級未量化的模擬輸出會繼續送往下級進行量化。得到的傳輸特性曲線如下圖所示。
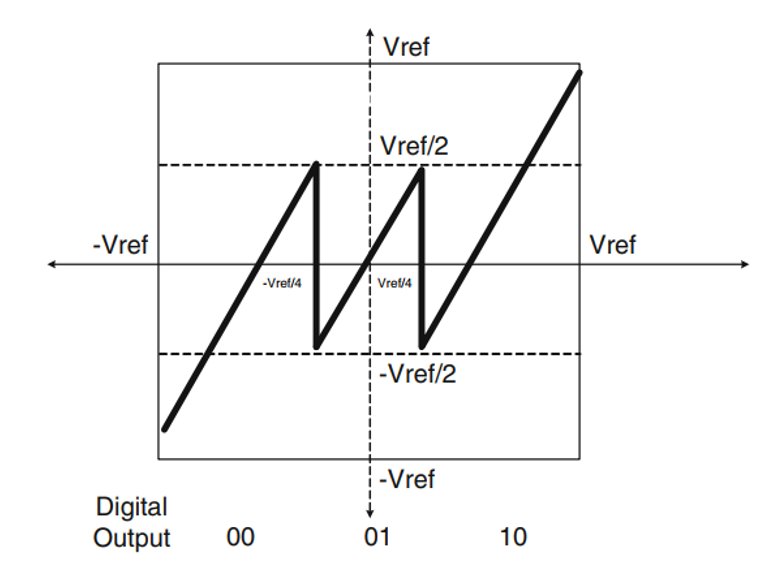
這個曲線就是非常經典的1.5-bit的單級結構了。前面我已經詳細介紹了它的由來,接下來我從另一個角度對其進行解釋。
一種更加簡單的理解方式就是認為接近轉折電壓0處的模擬輸入量非常容易由于比較器判決電壓的偏移而導致誤碼和失碼現象。因此在這附近單獨劃分一個區間,在當前級不進行判斷,對應于MDAC開關接到0電平(這里01對應于-Vref/2+Vref/4=Vref/4,由于曲線整體下移了Vref/4,因此接到0),也就是將模擬輸入原封不動放大后直接傳給下一級,由下一級進行判斷。
這種理解方式也可以認為是正確的,但解釋并不透徹,也并未說明可以直接進行普通二進制錯位相加的原理,因此要想深刻地理解此技術的原理應該去了解它的由來及演變過程。
審核編輯:黃飛
-
adc
+關注
關注
98文章
6438瀏覽量
544097 -
比較器
+關注
關注
14文章
1636瀏覽量
107102 -
輸出電壓
+關注
關注
2文章
1092瀏覽量
38024
發布評論請先 登錄
相關推薦
基于Ginkgo 2的ADC實現虛擬示波器功能
pipeline ADC的實現原理及基本結構筆記分享
pipeline_a2dp_sink_stream藍牙卡頓怎么解決?
Pipeline ADCs Come of Age
Pipeline ADCs Come of Age
14位Pipeline ADC設計的帶隙電壓基準源技術
修改V4L2的Video Pipeline的devicetree
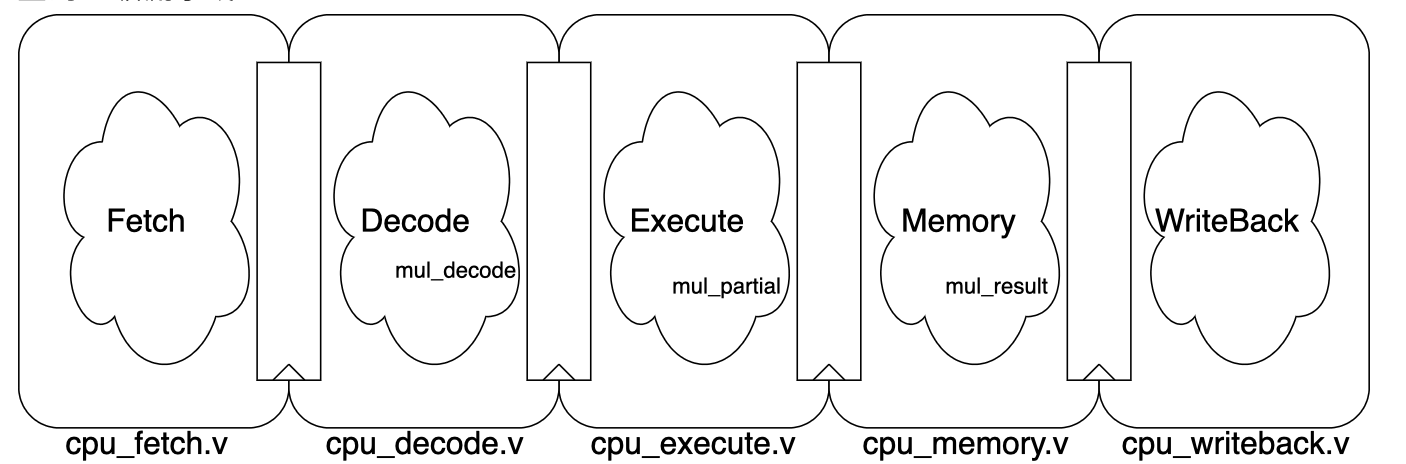
SpinalHDL里pipeline的設計思路
核芯互聯最新推出一款 Pipeline結構的模數轉換器(ADC)

國產ADC芯片——adc芯片的多種結構
pipeline ADC的實現原理及基本結構(1)




 pipeline ADC的實現原理及基本結構(2)
pipeline ADC的實現原理及基本結構(2)











評論