位錯(cuò)的應(yīng)力場(chǎng)和應(yīng)變力

位錯(cuò)在晶體中的存在，使其周?chē)悠x平衡位置，而導(dǎo)致點(diǎn)陣畸變和彈性應(yīng)力場(chǎng)的產(chǎn)生。

要進(jìn)一步了解位錯(cuò)的性質(zhì)，就須討論位錯(cuò)的彈性應(yīng)力場(chǎng)，由此可推算出位錯(cuò)所具有的能量、位錯(cuò)的作用力、位錯(cuò)與晶體其他缺陷間交互作用等問(wèn)題。

位錯(cuò)的應(yīng)力場(chǎng)

位錯(cuò)周?chē)膹椥詰?yīng)力場(chǎng)彈性體假設(shè)模型：

⑴晶體是完全彈性體；

⑵晶體是各向同性的；

⑶晶體中沒(méi)有空隙，由連續(xù)介質(zhì)組成。

01

刃型位錯(cuò)的應(yīng)力場(chǎng)

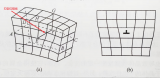
建立如圖1所示的刃型位錯(cuò)力學(xué)模型。該模型中圓筒的軸線對(duì)應(yīng)刃位錯(cuò)的位錯(cuò)線，圓筒的空心部分相當(dāng)于位錯(cuò)的中心區(qū)。

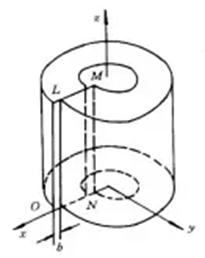
圖1 刃型位錯(cuò)應(yīng)力場(chǎng)

下面給出刃位錯(cuò)的應(yīng)力場(chǎng)公式：

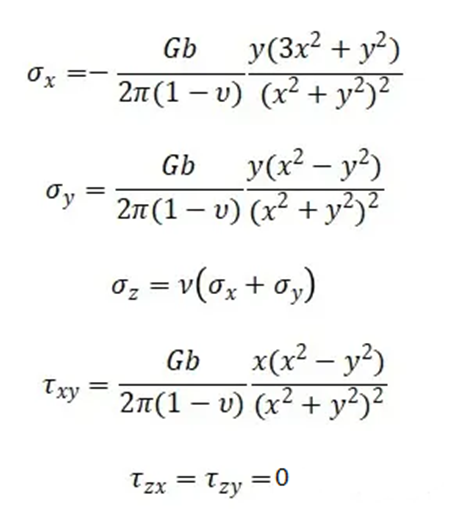
由上面所得結(jié)論可以看出：

σx與σy的符號(hào)相反。在滑移面上方，y>0，

σx為負(fù)（壓應(yīng)力）；在滑移面下方，y<0，

σx為正（拉應(yīng)力）。

②在y＝0處有

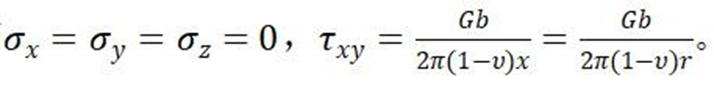
02

螺型位錯(cuò)的應(yīng)力場(chǎng)

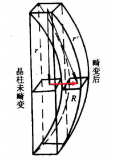
建立如圖2所示的螺型位錯(cuò)力學(xué)模型。從該模型可知，形成螺位錯(cuò)時(shí)只有軸向位移，沒(méi)有徑向和切向位移。

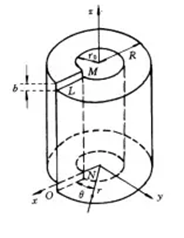
圖2 螺型位錯(cuò)應(yīng)力場(chǎng)

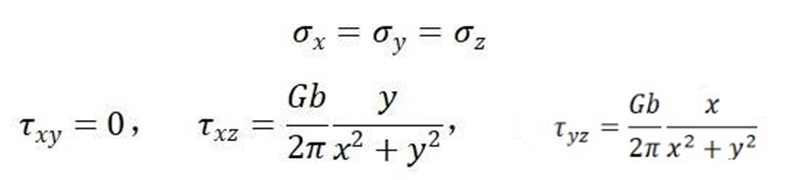
由上面的結(jié)果可知，螺位錯(cuò)的應(yīng)力場(chǎng)沒(méi)有正應(yīng)力分量，且剪應(yīng)力對(duì)稱(chēng)分布，在包含位錯(cuò)線的任何晶向平面上剪應(yīng)力都是Gb/2πr，與θ角無(wú)關(guān)。螺位錯(cuò)不引起晶體的膨脹或收縮。

所以，無(wú)論是刃型位錯(cuò)還是螺型位錯(cuò)，作用在滑移面上的沿滑移方向的剪應(yīng)力都可以寫(xiě)成是：

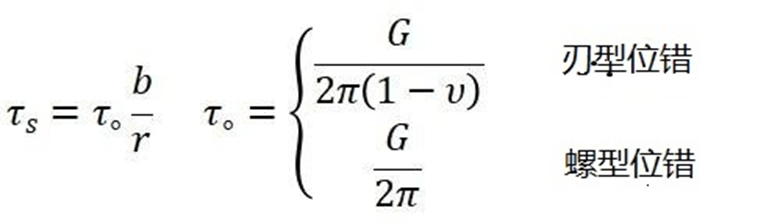
位錯(cuò)的應(yīng)變力

位錯(cuò)周?chē)c(diǎn)陣畸變引起彈性應(yīng)力場(chǎng)導(dǎo)致晶體能量的增加，這部分能量即為位錯(cuò)的應(yīng)變能。包括兩部分：Wtot=Wcore+Wel。

（1）位錯(cuò)核心能Wcore：在位錯(cuò)核心幾個(gè)原子間距ro=2|b|=2b以內(nèi)的區(qū)域，滑移面兩側(cè)原子間的錯(cuò)排能即相當(dāng)于位錯(cuò)核心能。錯(cuò)排能約占位錯(cuò)能的1/10，可忽略。

（2）彈性應(yīng)變能Wel：在位錯(cuò)核心區(qū)以外，長(zhǎng)程應(yīng)力場(chǎng)作用范圍所具有的能量，約占位錯(cuò)能的9/10。

由于位錯(cuò)在運(yùn)動(dòng)或與其他缺陷交互作用時(shí)，只有彈性能發(fā)生變化，因此，我們只關(guān)心各類(lèi)型位錯(cuò)的彈性能。

刃型位錯(cuò)的彈性能

下面使用做功法計(jì)算刃型位錯(cuò)的彈性能。

首先構(gòu)造一個(gè)刃位錯(cuò)的圓筒模型，如圖3所示。

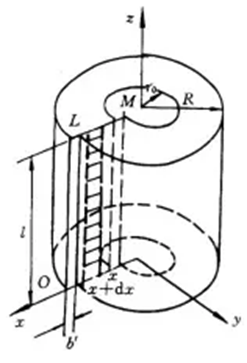
圖3 刃型位錯(cuò)的圓筒模型

假設(shè)在形成刃位錯(cuò)過(guò)程中的某一時(shí)刻滑移面兩邊的相互位移為b′，0 < b′ < b。此時(shí)滑移面上x(chóng)處產(chǎn)生的剪應(yīng)力為：τxy=τob′/x

此后，使滑移面兩邊的晶體相對(duì)位移由b′增至b′+db′，則此過(guò)程中外力反抗τxy

做功為：

對(duì)上式積分可得形成伯氏矢量為b的刃型位錯(cuò)過(guò)程中外力所做的總功，也既是位錯(cuò)的彈性能為：

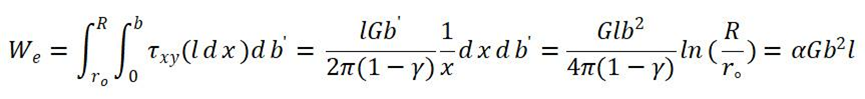
螺型位錯(cuò)的彈性能

采用與上面完全相同的做功法可以得到螺型位錯(cuò)的彈性能：

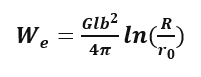
混合位錯(cuò)的彈性能

混合位錯(cuò)的彈性能應(yīng)該等于其螺型分量的彈性能和刃型分量的彈性能之和。因此，對(duì)混合位錯(cuò)做相應(yīng)分解，可以計(jì)算出混合位錯(cuò)的彈性能為：

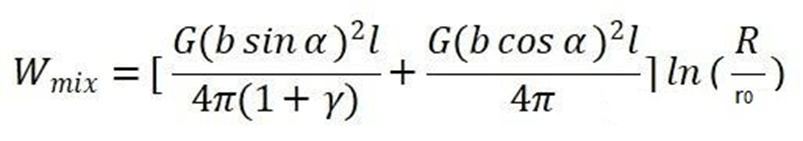
總之：

（1）位錯(cuò)的彈性應(yīng)變能Wel ∝ lnR，即隨R緩慢地增加，所以位錯(cuò)具有長(zhǎng)程應(yīng)力場(chǎng)。

（2）位錯(cuò)的能量是以單位長(zhǎng)度的能量來(lái)定義的，直線位錯(cuò)更穩(wěn)定，位錯(cuò)線有盡量變直和縮短其長(zhǎng)度的趨勢(shì)。

（3）位錯(cuò)的應(yīng)變能與b2成正比。位錯(cuò)的彈性應(yīng)變能可進(jìn)一步簡(jiǎn)化為一個(gè)簡(jiǎn)單的函數(shù)式：W=aGb2。

式中W為單位長(zhǎng)度位錯(cuò)線的彈性應(yīng)變能，G是剪切模量，b是伯氏矢量，α=1/4πl(wèi)nR/r0 其中R是晶體的外徑、r0是位錯(cuò)核心的半徑，系數(shù)a由位錯(cuò)的類(lèi)型、密度（R值）決定，其值的范圍為0.5-1.0。

意義：上式表明W ∝ b2，故可用伯氏矢量的大小來(lái)判斷晶體哪些地方最容易形成位錯(cuò)。

審核編輯：劉清