來源：德思特測量測試德思特干貨｜如何使用SBench 6對數字化儀采集信號進行處理？（三）——快速傅立葉變換（FFT）

原文鏈接：https://mp.weixin.qq.com/s/mYS1iDXFNVfReCGGtF78mw

歡迎關注虹科，為您提供最新資訊！

#信號采集 #信號處理 #測量測試

上一篇文章介紹了德思特SBench 6的平均運算功能。本章將繼續為大家介紹SBench 6的快速傅立葉變換（FFT）。

前文回顧：https://mp.weixin.qq.com/s/j-iN_2Jrn9ZHGMaaAYsDJg

快速傅立葉變換（ FFT ）

快速傅立葉變換（FFT）將獲取的波形從時域（幅度對時間）映射到頻譜域（幅度對頻率）。這使得用戶可以觀察構成信號的頻率成分。FFT本身并不能直接改善信號質量，但它能顯示信號的頻率成分結構，并提供了如何移除不需要的頻譜成分的信息。

FFT產生的頻譜有一個離散的時間軸，就像時域信號有離散的采樣時間一樣。頻譜中的譜線，通常稱為“bins”或“cells”，每個譜線之間由分辨率帶寬（f）隔開，而分辨率帶寬與采集到的原始信號長度成反比，因此，要增加FFT頻譜的頻率分辨率，必須增加采集的原始信號長度。而頻譜顯示的總頻率范圍，或者說頻率跨度，是原始信號采樣率的一半，因此，要增加總頻率跨度，也必須增加采樣率。

在德思特SBench 6軟件中，FFT結果的縱軸縮放可以設為線性單位伏特，也可以是對數單位分貝（dB）。對數刻度可以參考數字化儀的滿偏刻度（dBFS）、1 毫瓦（dBm）、1 微伏（dbμV）或設為針對假定載波頻譜中的最大峰值（dBc）。

（1）權重函數

理論上的傅立葉變換假設輸入記錄的長度為無窮大。有限的采樣長度則會在頻域邊緣引入不連續性，為頻域引入偽頻率，并一定程度扭曲實際的頻譜。例如，當信號的開始和結束相位不同，或者信號頻率落在兩個相鄰的譜線之間時，使頻譜變寬。

頻譜展寬，以至于擴展到許多相鄰的頻帶，稱為泄漏。對于這種問題的理論應對方法是確保在顯示網格內包含整數個周期，或在邊緣處不出現不連續性。兩者都需要信號波形頻率和數字化采樣率之間非常精確的同步，并且需要準確地設置采集長度，這通常只可能在實驗室中實現，而不能作用于真實世界的信號。另一種方法是使用窗函數（加權）來平滑信號的邊緣。

為了盡量減少這些負面影響，對獲取的信號應用加權函數，使記錄的端點為零。德思特SBench 6軟件中的FFT功能為用戶提供八種加權函數的選擇，而這些加權函數則可以改變譜線的形狀。對此沒什么概念的讀者，可以把它想象為組合到一起的一些列并行的理想帶通濾波器，這些濾波器之間的頻率間距為分辨率帶寬，而加權函數則會影響濾波器頻率響應的形狀。圖1比較了四種最常用的加權函數對應的頻率響應。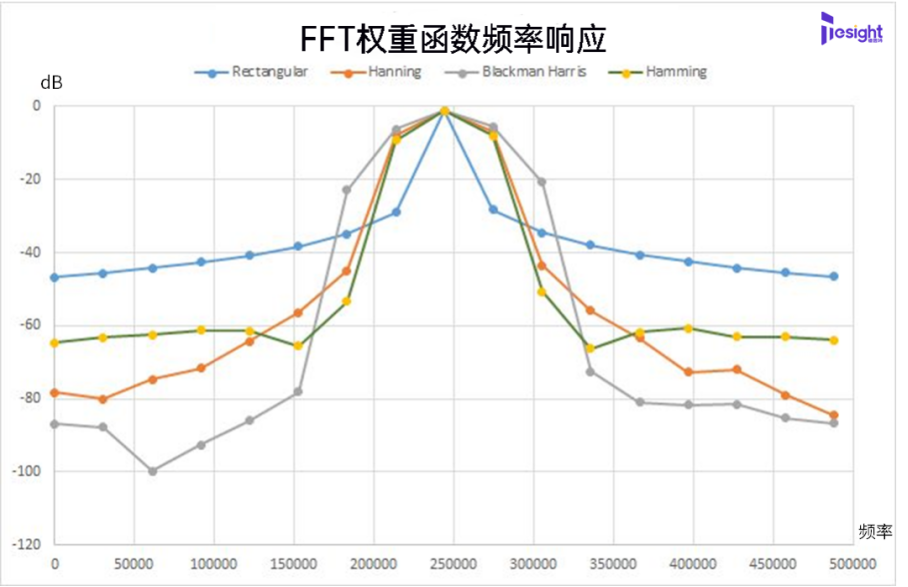

圖1：四種最常用的加權函數的譜形狀比較

理想情況下，主瓣應盡可能窄，且兩側平坦，以代表真實的頻譜成分，而所有旁瓣應無限衰減。窗函數類型定義了在FFT處理中使用的等效濾波器的帶寬和形狀。表1中展示了頻譜響應的最大旁瓣幅度。較大的旁瓣電平將有助于區分密集的頻譜成分。

表1：不同加權函數的關鍵特性

如前所述，FFT結果的頻率軸是離散的，具有以分辨率帶寬的倍數間隔的頻點。如果輸入信號頻率落在兩個相鄰的譜線之間，能量將被分配到兩個譜線中，且峰值幅度將降低。這被稱為柵欄效應或波浪狀效應，而擴寬頻譜響應可以減少幅度變化。表1中的柵欄損失列給出了不同加權函數該效應幅值。

同時，加權函數還會影響頻譜響應的帶寬。等效噪聲帶寬（ENBW）說明了相對于矩形窗加權帶寬的相對變化。將功率譜歸一化到測量帶寬（功率譜密度）需要將功率譜除以ENBW與分辨率帶寬的積（f??ENBW）。

相干增益描述了給定加權函數相對于矩形窗加權的頻譜幅度變化。這是一個應用在所有頻率上的固定增益，可以很容易地歸一化。

矩形窗加權函數是采集信號沒有任何加權的響應。它具有最窄的帶寬，但旁瓣幅值則相當高。由于采集時域記錄中的所有點的幅度響應都是均勻的，它常用于具有瞬態性質的信號（或相對記錄總長短得多的信號）。當需要以最佳頻率精度進行分析時，也會使用它。

Hanning和Hamming加權函數具有良好的通用的頻率響應，能提供較好的頻率分辨率以及合理的旁瓣響應。Blackman-Harris則旨在獲得最佳幅度精度和優秀的旁瓣抑制。

（2）FFT應用實例

圖2展現了一個典型的FFT應用實例。在該實例中，我們使用寬帶的儀器級麥克風和德思特TS-M4i系列14位數字化儀，獲得了超聲波測距儀的信號。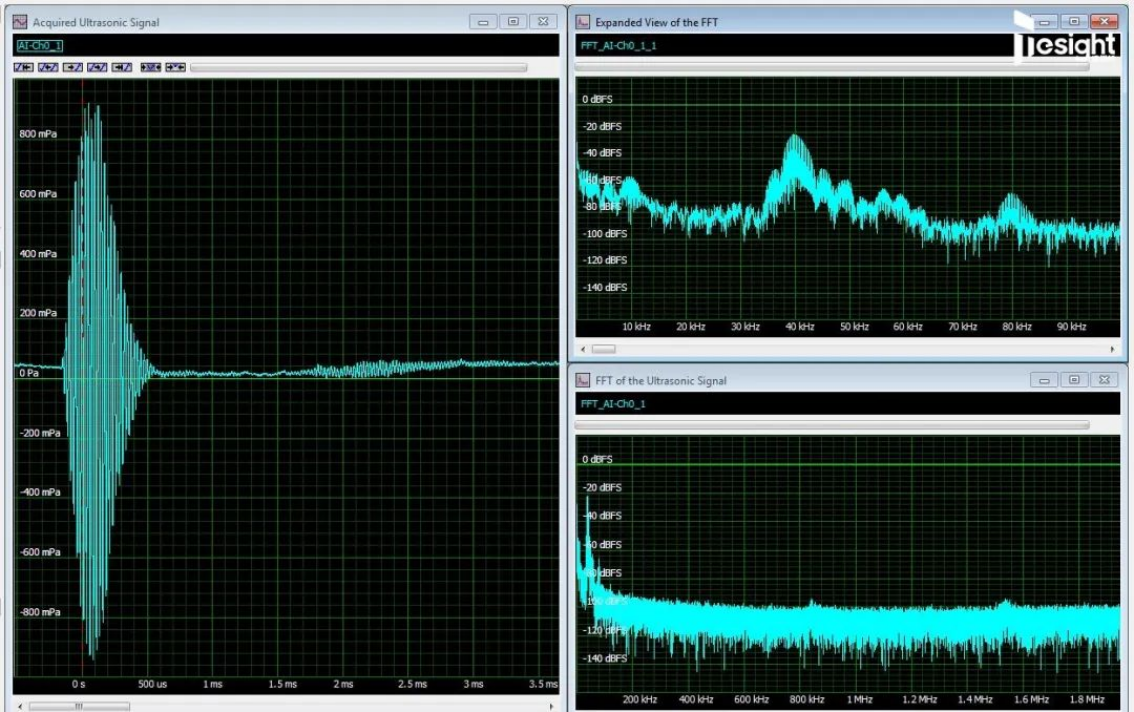

圖2：40 kHz的超聲波脈沖（左）及其FFT結果（右下全頻段，右上局部放大）

采集到的時域信號在左窗格中。時域記錄包含了在3.90625 MS/s采樣率下采集到的16384個樣本點，持續時間為4.2毫秒。得到的FFT結果（右窗格）共有8192條譜線，每條譜線之間間隔238 Hz分辨率帶寬（記錄時長的倒數），總頻率跨度為1.95 MHz（采樣率的一半）。其中，右下角的頻譜是全頻段總覽圖，右上角則是局部放大視圖，只顯示了前100 kHz頻率范圍的內容，以便更好地觀察主要頻譜成分。

FFT能幫助我們更好地理解構成這個信號的成分。首先我們看時域，可以知道這是一個持續時間小于采集記錄長度的瞬態信號，在這種情況下我們選用了矩形窗進行加權。FFT結果中幅值最大的頻率成分，明顯就是我們的主要信號——40 kHz左右的脈沖。而在80 kHz附近頻率的一個小峰，則是40 kHz信號成分的二次諧波。其幅度大約比40 kHz信號成分低45 dB。此外，在0~10 kHz之間也有很多低頻干擾成分，其中最高的、接近DC的那部分，對應的是設備所在房間中的環境噪聲。

在該實例中，我們的目標是能夠測量發射脈沖和40 kHz回波之間的時延。為了實現這一點，我們需要改進這個測量過程。第一步，我們希望移除頻譜中40 kHz成分之外的其它成分。現在我們將帶著這個目標，來進行濾波器的設置。

（3）濾波

在德思特SBench 6專業版軟件中，我們提供了低通、帶通或高通選項的有限沖激響應(FIR)數字濾波器。通過輸入所需的濾波器類型、截止頻率或頻率，以及濾波器階數，用戶可以直接在圖形界面中創建這些濾波器。SBench 6軟件會在濾波器無法實現時給出提示，并提出解決建議。或者，您也可以輸入從其他來源獲取的濾波器系數。我們將這些濾波器應用于采集到的信號，然后將濾波結果與原始采樣結果或平均采樣結果進行比較。在圖3中，應用的帶通FIR濾波器截止頻率為30和50 kHz，以幫助提取目標信號。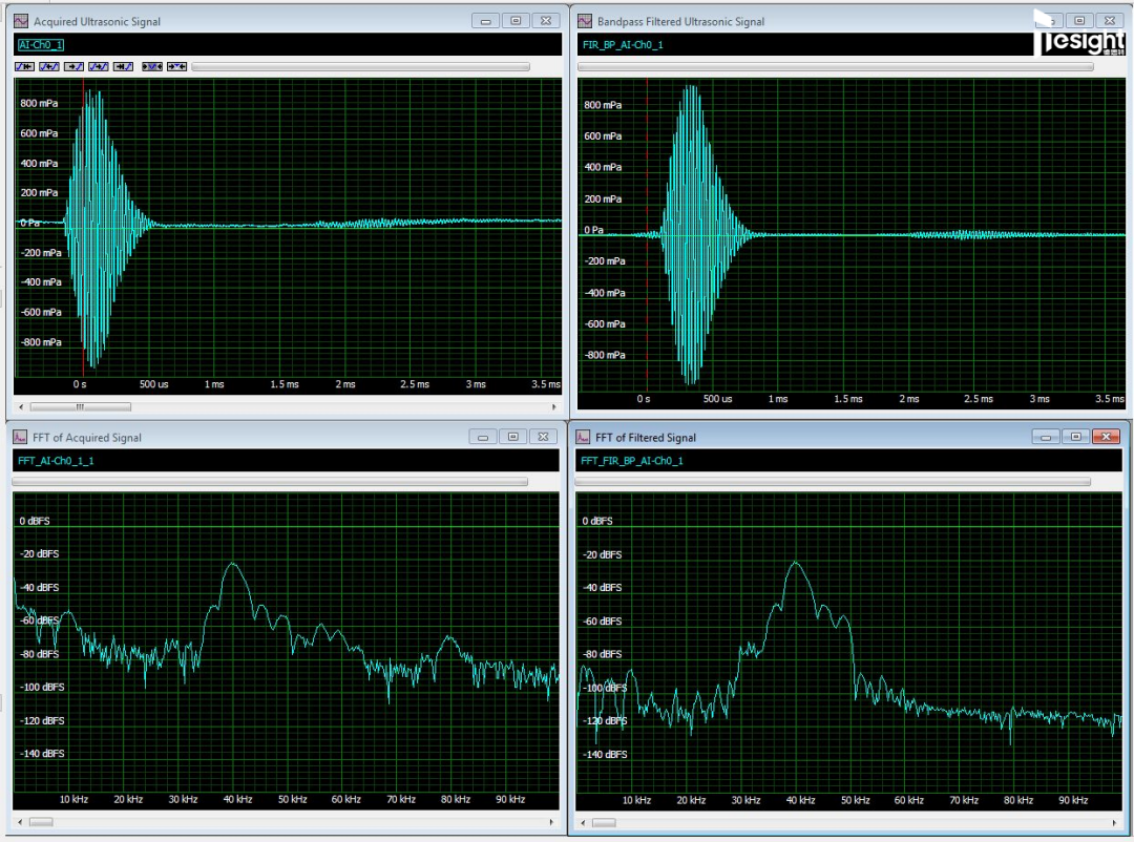

圖3：原始波形和濾波后信號及其FFT結果的對比

左上角的窗格顯示了原始波形，下面對應我們之前看到的原始信號FFT結果。右上角的窗格則為通過帶通濾波后的波形，濾波信號的FFT結果在右下角的窗格中。可以發現，帶通濾波器消除了低頻拾取噪聲和80 kHz位置的二次諧波。濾波后的信號在時間域視圖現在有了一個相對平坦的基線，從而能使反射信號更清楚地分辨出來，而這就是我們濾波處理的目標。由此我們也可以看出FFT對深入了解信號提供的幫助。