正弦交流電的三要素是振幅、頻率和初始相位。

首先，我們來探討一下振幅。振幅表示正弦波的最大偏離值，即波峰的高度或波谷的低度。在電路中，交流電的振幅通常表示為電壓或電流的最大值。通常情況下，我們使用有效值來表示交流電的振幅。有效值是指使得交流電的功率在純電阻電路中保持不變時所需的直流電壓或電流的大小。對于正弦波，其有效值等于振幅的約0.707倍。有效值通常用字母RMS（均方根值）來表示。

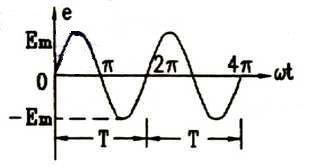
然后，我們來研究一下頻率。頻率是指正弦波每秒鐘完成的周期數(shù)，單位為赫茲（Hz）。在電路中，我們通常用交流電的頻率來描述電路的工作狀態(tài)。正弦交流電的頻率決定了電路中電壓和電流的周期性變化。在實際應用中，交流電的頻率通常為50Hz或60Hz。頻率的倒數(shù)被稱為周期，即每個周期完成的時間。

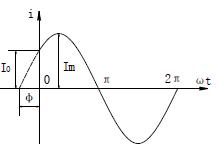
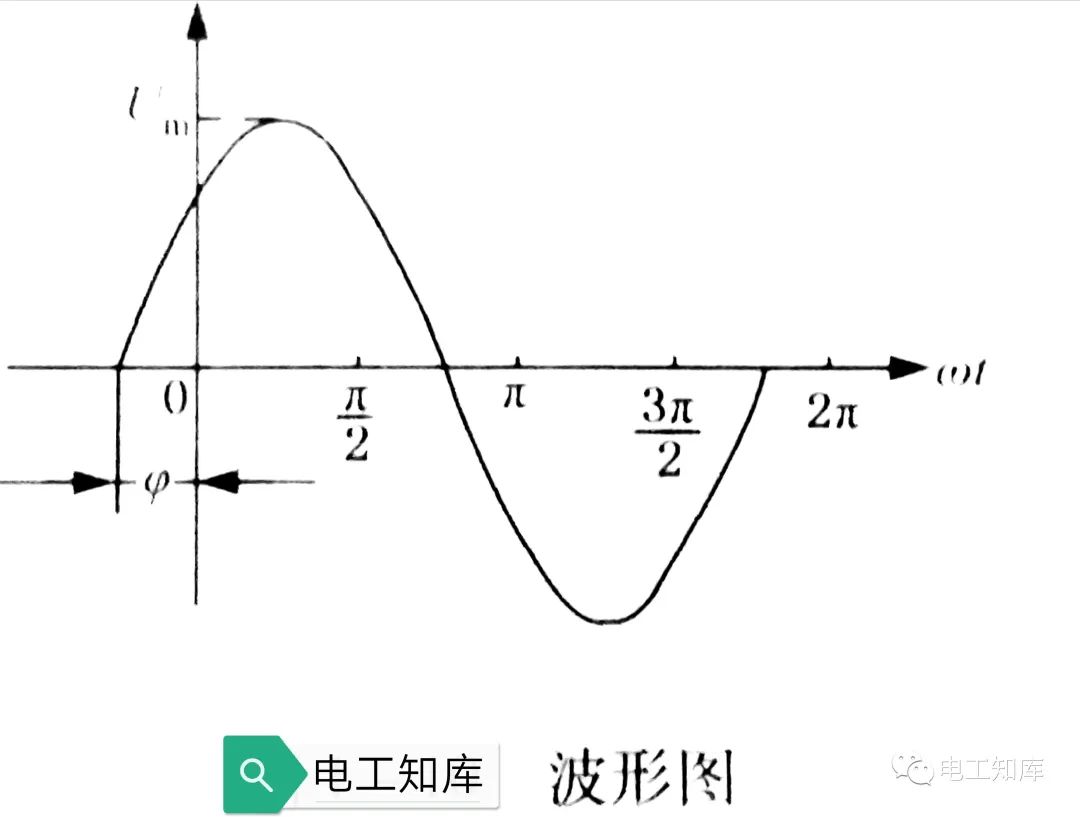
最后，讓我們研究一下初始相位。初始相位是指正弦波在時間軸上的位置，它決定了正弦波的起點。初始相位通常用弧度來衡量，取值范圍在0到2π之間。在電路中，交流電的初始相位對電路的行為有很大影響。不同的初始相位將導致電壓和電流之間存在不同的相位差，從而影響電路中的功率傳遞和能量轉(zhuǎn)換。

接下來，我們詳細討論一下如何求解正弦交流電的有效值。

為了求解正弦交流電的有效值，我們需要先了解正弦波的特性。正弦波是一種連續(xù)的周期性波動，其數(shù)學表達式為V(t) = Vm * sin(ωt + φ)，其中V(t)表示時刻t的電壓值，Vm表示振幅，ω表示角頻率，t表示時間，φ表示初始相位。

為了求解正弦交流電的有效值，我們可以利用該波形的特性進行計算。首先，我們需要求得正弦交流電的平方值，即V(t)的平方。因為正弦波在一個周期內(nèi)的值是對稱的，所以平方后的值是正的。我們可以利用此特性將一個周期內(nèi)的面積分為兩部分，然后再將其相加以得到整個周期內(nèi)的面積。

對于正弦波電壓，其平方值為V(t)^2 = (Vm * sin(ωt + φ))^2 = Vm^2 * sin^2(ωt + φ)。

接下來，我們需要對一個周期的平方值進行積分，并求得其平均值。平均值即為有效值的平方，我們可以通過將平均值開方來得到正弦交流電的有效值。

這里有一個非常重要的數(shù)學公式：sin^2(θ) = (1 - cos(2θ)) / 2。我們可以將平方波的積分用這個公式來簡化計算過程。

我們將正弦波的平方值進行積分，得到一個周期的面積。由于正弦波是周期性的，我們可以將其分為正周期和負周期兩部分進行計算。假設一個周期的長度為T，則正周期的積分為∫[0, T/2] (Vm^2 * sin^2(ωt + φ)) dt，負周期的積分為∫[T/2, T] (Vm^2 * sin^2(ωt + φ)) dt。

根據(jù)上述數(shù)學公式，我們可以將正周期的積分中的sin^2項轉(zhuǎn)換為cos項。這樣，正周期的積分可變?yōu)椤襕0, T/2] (Vm^2 * 0.5 * (1 - cos(2(ωt + φ)))) dt。

我們可以繼續(xù)化簡積分式，得到正周期的積分為Vm^2 * T / 4。

同樣地，負周期的積分也為Vm^2 * T / 4。

接下來，我們將正周期和負周期的積分相加，得到一個周期的積分為Vm^2 * T / 2。

最后，我們求取平均值，即將一個周期的積分除以周期長度T，得到平均值為Vm^2 / 2。

平均值即為正弦交流電的有效值的平方。我們將其開方，即可得到正弦交流電的有效值。

綜上所述，正弦交流電的有效值的計算公式為：Vrms = sqrt(Vm^2 / 2) = Vm / sqrt(2)。

這就是正弦交流電的有效值的求解方法。

總結(jié)起來，正弦交流電的三要素是振幅、頻率和初始相位。振幅表示正弦波的最大偏離值，有效值是指在純電阻電路中保持交流電功率不變時的直流電壓或電流大小。頻率表示正弦波每秒完成的周期數(shù)，決定了電路中電壓和電流的周期性變化。初始相位決定了正弦波的起點，對電路中的功率傳遞和能量轉(zhuǎn)換有影響。