正弦交流電的周期與角頻率的關系是一種基本的物理關系，涉及到電學和物理學的一些基本概念和原理。在這篇文章中將詳細介紹周期和角頻率的概念、它們的數學定義和計算方法，以及它們之間的關系。該文章將包括周期和角頻率在電路中的應用、周期與頻率之間的關系、在不同電路條件下周期和角頻率的變化等方面的內容。

一、概念和定義

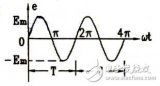
周期是指某個事件重復發生所經歷的時間間隔。在正弦交流電中，周期是指電流或電壓在一定時間內完成一個完整的振蕩過程所需要的時間。周期的單位是秒（s）。

角頻率是指正弦交流電振蕩過程中角度的變化速度。在正弦函數中，角頻率描述了正弦函數的周期性。角頻率的單位是弧度/秒（rad/s）。

周期和角頻率之間的關系可以通過以下公式表示：

頻率 f = 1 / T

角頻率 ω = 2πf

其中，T表示周期，f表示頻率，ω表示角頻率，π是一個常數，約等于3.14。

二、計算方法和示例

正弦交流電的周期和角頻率可以通過電壓或電流的波形圖來計算。以電流為例，可以通過測量電流波形的時間來計算周期，然后再通過公式計算角頻率。

例如，某個電流波形的周期為0.02秒，那么根據公式可以計算出頻率為1 / 0.02 = 50Hz。再根據公式計算出角頻率為2π × 50 ≈ 314.16 rad/s。

三、周期和角頻率在電路中的應用

周期和角頻率的概念在電路中具有重要的應用價值。首先，周期和角頻率是計算電路中各種參數的基礎，例如頻率響應、阻抗、電流和電壓等。其次，周期和角頻率也是計算交流電功率的重要參數。

在電路中，周期和角頻率還可以幫助我們分析電路的穩定性和振蕩頻率。通過計算電路中的周期和角頻率，我們可以確定電路是否處于穩定狀態，以及電路是否能夠產生有效的交流信號。

四、周期與頻率之間的關系

周期和頻率是兩個基本的物理量，在正弦交流電中有一種簡單的數學關系。如前所述，頻率可以通過周期的倒數來計算。反過來，周期也可以通過頻率的倒數來計算。因此，周期和頻率具有互為倒數的關系。

例如，頻率為100Hz的正弦交流電的周期可以通過計算1 / 100 = 0.01秒得出。相反，周期為0.01秒的正弦交流電的頻率可以通過計算1 / 0.01 = 100Hz得出。這表明周期和頻率之間存在一種簡單的互相關系。

五、周期和角頻率的變化

周期和角頻率在不同的電路條件下可能會發生變化。在電容和電感電路中，周期和角頻率可以受到電阻、電感或電容的影響。

當電容和電感的數值變大時，周期和角頻率會相應地變大。這是因為電容和電感的數值越大，電路的振蕩時間就越長，所以周期和角頻率都會增大。

另一方面，當電阻的數值增大時，周期和角頻率會減小。這是因為電阻會減弱電路中的振蕩效果，使得周期和角頻率減小。

當周期和角頻率發生變化時，電路中的電流和電壓也會隨之變化。例如，當周期變大時，電流和電壓的振幅會變小；當角頻率變小時，電流和電壓的頻率也會變小。

六、正弦交流電的周期與角頻率對電路中電流和電壓的影響

正弦交流電的周期和角頻率對電路中的電流和電壓有著重要的影響。不同的周期和角頻率可以產生不同的電壓和電流波形。

當周期較短或角頻率較大時，電流和電壓的變化速度較快，產生的電流和電壓波形比較緊湊。當周期較長或角頻率較小時，電流和電壓的變化速度較慢，產生的電流和電壓波形比較寬松。

另外，周期和角頻率還會影響電路中電流和電壓的幅值。當周期較短或角頻率較大時，電流和電壓的幅值較大；當周期較長或角頻率較小時，電流和電壓的幅值較小。

本文詳細介紹了正弦交流電的周期與角頻率的概念、定義、計算方法和它們之間的關系。周期和角頻率是正弦交流電中的兩個重要物理量，對于電路中電流和電壓的計算、分析和應用具有重要意義。周期和角頻率在電路中的應用包括頻率響應、阻抗計算、功率計算、穩定性分析等。周期和角頻率還與電路的電容、電感、電阻有關，它們會隨著電路條件的改變而發生變化。