本文簡單介紹了頻率濾波的原理、傅立葉變換與頻域濾波以及濾波應用。

干涉圖是光學實驗中常見的現象，它反映了光波相互疊加形成的干涉條紋，展現了光的波動性質。在干涉圖的處理和分析中，頻率濾波起著至關重要的作用。讓我們一起深入探討干涉圖濾波的奧秘吧！

為了增強干涉圖圖像，減少外界因素對干涉儀干涉現象（由兩個或多個受控波前產生的干擾）引起的噪聲，采用低通技術作為預處理濾波步驟。干涉圖平滑和去噪是低通濾波器在干涉測量中應用的主要目的。濾波技術可以分為空間域或頻域，其中A空間濾波直接應用于干涉圖圖像，像素到像素，而B頻率濾波通常在傅里葉域中執行。帶通和帶阻是一些可以應用于傅里葉域的濾波技術，這些濾波器用于衰減特定噪聲的某些頻率。

頻率濾波原理與方法

頻率濾波的原理是通過將圖像的頻域表示與某種濾波函數進行卷積操作，以實現對特定頻率成分的調整或抑制。常見的頻率濾波包括低通濾波、高通濾波、帶通濾波和帶阻濾波。例如，低通濾波可用于去除圖像中的高頻噪聲，而高通濾波則可增強圖像的邊緣特征。

圖 1. 空間低通濾波器：(a) 原始 ronchigram，(b) 采用高斯、二次、三角函數和平均掩碼，以及 3*3、5*5 和 7*7 卷積掩碼大小。

傅立葉變換與頻域濾波

干涉圖的頻域濾波通常是在傅立葉域進行的。傅立葉變換可以將圖像從空間域轉換到頻率域，從而使得頻率信息更加清晰可見。通過對傅立葉變換后的頻譜進行濾波操作，可以實現對干涉圖的精確處理和優化。頻域濾波通常在傅里葉域中進行。傅里葉變換反映了從空間到頻域的變化。方程（1）和方程（2）表示一對二維離散傅里葉變換。

方程（1）

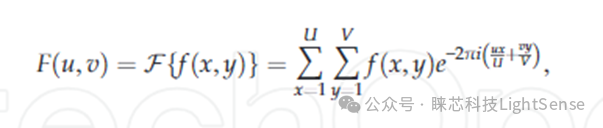
方程（2）

?

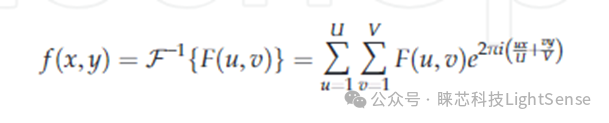其中 (u, v)是頻率坐標，U、V是圖像大小（以像素為單位），F 和 F ?1分別是傅里葉變換和傅里葉逆變換算子。

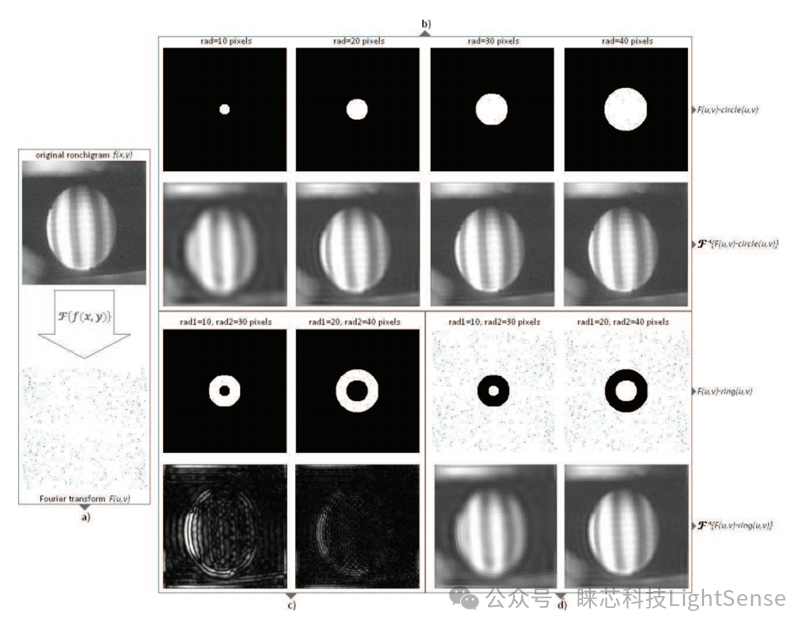
圖 2. 頻域濾波：(a) 原始 ronchigram 的傅立葉變換，(b) 不同半徑的低通濾波的二進制圓掩模，（c）具有兩種尺寸的二進制圓掩模的帶通濾波，以及（d）具有兩種尺寸的帶阻濾波二元環掩模。

濾波應用與效果展示

在實際應用中，頻率濾波在干涉圖的處理中發揮著重要作用。通過不同類型的濾波操作，我們可以調整干涉圖的清晰度、對比度和細節等方面，從而獲得更加清晰和準確的圖像信息。本文結合實例展示了低通、帶通和帶阻濾波在干涉圖處理中的效果，如圖2所示。

結語

頻率濾波是干涉圖處理中的一項重要技術，它不僅可以優化干涉圖的質量，還可以提高圖像的可讀性和分析性。通過深入學習和掌握頻率濾波的原理和方法，我們可以更好地理解和利用干涉圖，為光學研究和實驗提供更多可能性。

審核編輯：劉清