1. 引言
之前我們簡(jiǎn)單介紹了基于差壓的流量傳感器,這次我們要開始基于超聲的流量計(jì)。超聲流量計(jì)是一種測(cè)量液體或氣體流量的儀器,其工作原理基于超聲波在介質(zhì)中傳播的特性。這種流量計(jì)可以在無需接觸或干擾流體本身的情況下進(jìn)行測(cè)量,因此被廣泛應(yīng)用于各種工業(yè)環(huán)境,尤其是在需要無接觸或無損測(cè)量的場(chǎng)合。
超聲流量計(jì)的應(yīng)用領(lǐng)域非常廣泛,從水處理和污水處理設(shè)施,到化工和石油行業(yè),再到食品和飲料生產(chǎn)線。這些設(shè)備還在航空、電力和熱力行業(yè)中發(fā)揮著關(guān)鍵作用,幫助這些行業(yè)的專業(yè)人士監(jiān)控系統(tǒng)的效率,評(píng)估設(shè)備的性能,以及確保工藝流程的連續(xù)性。
此外,超聲流量計(jì)還在醫(yī)療領(lǐng)域有著重要應(yīng)用。例如,醫(yī)護(hù)人員可以利用超聲流量計(jì)監(jiān)測(cè)血液或藥物的輸送速度,對(duì)心血管疾病的診斷和治療中起到關(guān)鍵作用。 而今,隨著科技的不斷發(fā)展,超聲流量計(jì)的準(zhǔn)確性和可靠性得到了大幅提升,讓我們能夠在不同的場(chǎng)景和環(huán)境中,對(duì)流體流動(dòng)有著更精確的控制和理解。
2. 相關(guān)性原理
相關(guān)性是一個(gè)統(tǒng)計(jì)學(xué)術(shù)語,用來描述兩個(gè)或多個(gè)隨機(jī)變量之間的統(tǒng)計(jì)關(guān)系。在信號(hào)處理中,原則上這個(gè)關(guān)系也可以不必非要是線性的,相關(guān)性分析也可以衡量?jī)蓚€(gè)信號(hào)的非線性關(guān)系。 相關(guān)性的計(jì)算通常通過相關(guān)系數(shù)(Pearson相關(guān)系數(shù)為最常用的一種)來實(shí)現(xiàn)。
相關(guān)系數(shù)的值范圍在-1到1之間,0表示兩個(gè)變量獨(dú)立無關(guān),-1表示兩個(gè)變量完全負(fù)相關(guān),1表示兩個(gè)變量完全正相關(guān)。 在信號(hào)處理中,通常會(huì)用到互相關(guān)(Cross-Correlation)函數(shù),它是對(duì)兩個(gè)信號(hào)的相似性進(jìn)行度量。這在很多應(yīng)用中非常有用,比如在無線通信中的信號(hào)識(shí)別,圖像處理中的模式匹配,以及地球物理勘探中地震波的分析等。
計(jì)算互相關(guān)函數(shù)的公式為:
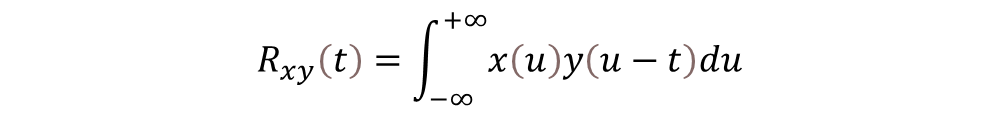
其中,x和y分別為兩個(gè)信號(hào),Rxy(t)為在延時(shí) t 時(shí)的互相關(guān)值。 在離散時(shí)間序列中,可以用求和代替積分進(jìn)行計(jì)算。 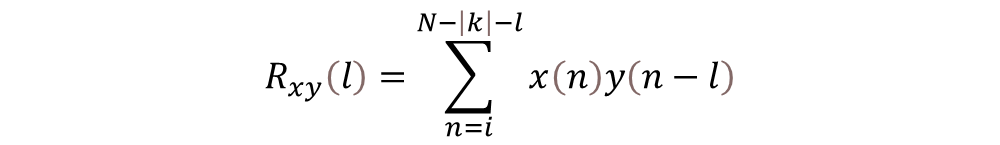
其中,l>=0時(shí),i=l,k=0,并且l<0時(shí),i=0,k=l。
以上公式中,t和l表示時(shí)間的移位;下標(biāo)xy的順序,表示一個(gè)變量或序列相對(duì)于留一個(gè)變量或序列的移位方向:上面兩個(gè)等式中,變量x或者序列x(n)未移動(dòng),而y或者y(n)在時(shí)間上移動(dòng)了t或l個(gè)單位:向右移動(dòng)則t或l為正;向左移動(dòng)則t或l為負(fù)。
數(shù)據(jù)相關(guān)性分析對(duì)于有加性噪聲的信號(hào)分析有其獨(dú)到的特點(diǎn)。
舉現(xiàn)成的栗子[1]: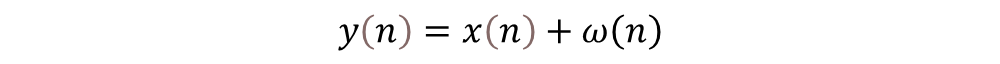
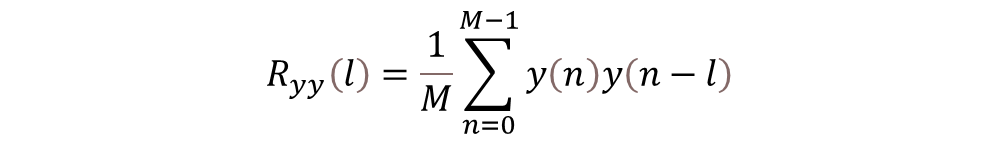
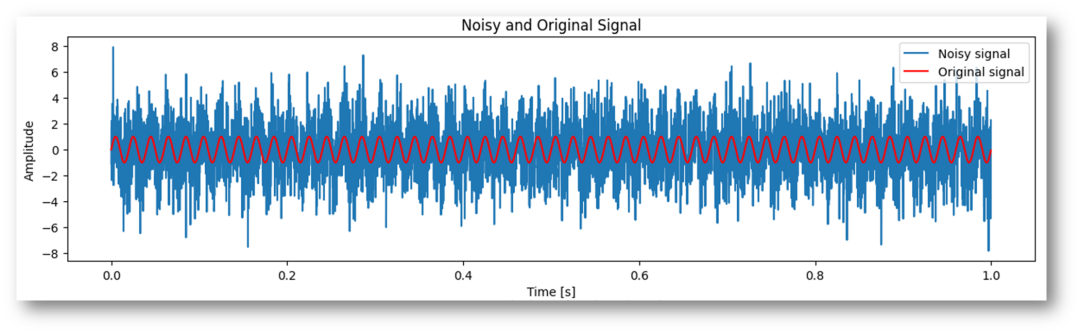
圖-1加性噪聲下的周期信號(hào)
這里x(n)(紅色部分正弦線條)是一個(gè)周期性的序列,周期N未知,ω(n)表示隨機(jī)噪聲,藍(lán)灰色信號(hào)線為y(n)=x(n)+ω(n)。我們?cè)趺慈チ私庠搸г肼曅盘?hào)y(n)的周期?[1](這里省掉了對(duì)于周期信號(hào)相關(guān)性計(jì)算特點(diǎn)的陳述)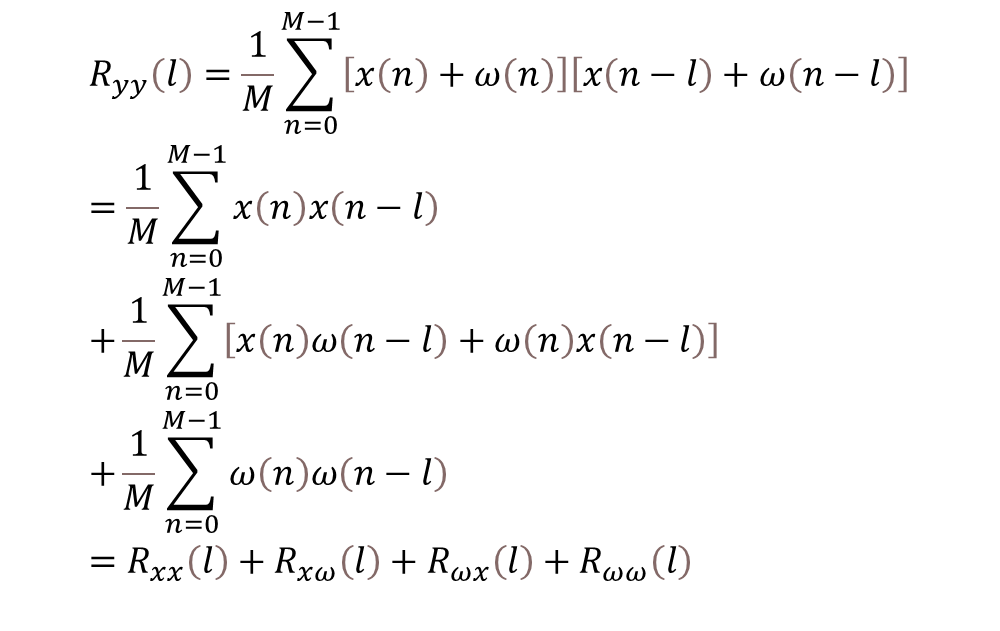
盡管小編也很想花些篇幅來說明相關(guān)性應(yīng)用的特點(diǎn),限于篇幅,我們對(duì)于上面的周期為N的信號(hào)自相關(guān)的結(jié)果中,Rxx在l=0,N和2N等處有相對(duì)較大的峰值;信號(hào)x(n)和加性噪聲ω(n)的互相關(guān)Rxω和Rωx相對(duì)很小;而隨機(jī)噪聲信號(hào)的自相關(guān)Rωω序列,除了在l=0處有峰值外(每個(gè)對(duì)應(yīng)點(diǎn)自相乘后累加),其余點(diǎn)將很快衰減到0。 這里忘了說明:周期信號(hào)的自相關(guān)序列也是一個(gè)同周期的序列。也就是如下公式所示的周期為N的序列x(n)自相關(guān)[1]:
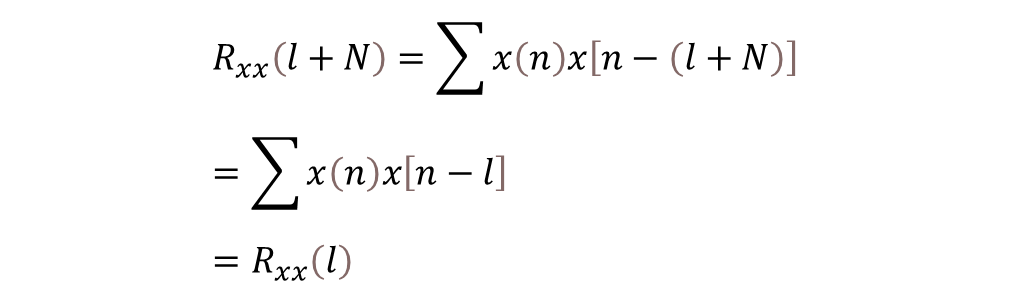
在這種情況下,我們計(jì)算y(n)的自相關(guān)序列后,可以得到噪聲淹沒下的周期,如下的圖示的每2個(gè)紅點(diǎn)之間的時(shí)間所代表的周期結(jié)果: 噪聲下的周期信號(hào)的相關(guān)性周期檢查演示代碼如下所示:
import numpy as np import matplotlib.pyplot as plt from scipy.signal import find_peaks # 創(chuàng)建一個(gè)正弦信號(hào) T = 1/50 # 50Hz信號(hào),周期為1/50,這里實(shí)際設(shè)置為0.02秒 fs = 5000 # 抽樣頻率 t = np.arange(0, 1, 1/fs) # 持續(xù)時(shí)間為1秒 signal = np.sin(2 * np.pi * 50 * t) # 添加噪聲 noise = np.random.normal(0, 2, signal.shape) noisy_signal = signal + noise # 計(jì)算信噪比SNR,以dB表示 SNR = 10 * np.log10(np.mean(signal**2) / np.mean(noise**2)) print('SNR: {:.2f} dB'.format(SNR)) # 計(jì)算并顯示帶噪聲的正弦波和清潔的正弦波 plt.figure(figsize=(12, 8)) plt.subplot(2, 1, 1) plt.plot(t, noisy_signal, label='Noisy signal') plt.plot(t, signal, 'r', label='Original signal') plt.legend(loc='upper right') plt.xlabel('Time [s]') plt.ylabel('Amplitude') plt.title('Noisy and Original Signal') # 計(jì)算自相關(guān)函數(shù) auto_corr = np.correlate(noisy_signal, noisy_signal, mode='full') # 找到自相關(guān)函數(shù)的峰值檢查閾值[max()/12]來估計(jì)周期 auto_corr = auto_corr[auto_corr.size // 2:] #取相關(guān)信號(hào)結(jié)果的后半截?cái)?shù)據(jù) peaks, _ = find_peaks(auto_corr, height=auto_corr.max()/12, distance=fs/60) # 最小距離設(shè)置為一個(gè)頻率60Hz的周期 estimated_period = np.diff(peaks) / fs print('Estimated period: {:.2f} s'.format(estimated_period.mean())) # 繪制自相關(guān)函數(shù)并顯示峰值 plt.subplot(2, 1, 2) plt.plot(t, auto_corr / fs, 'g') # 除以fs以便時(shí)間以秒為單位 plt.plot(peaks / fs, auto_corr[peaks] / fs, 'ro') plt.xlabel('Time delay [s]') plt.ylabel('Autocorrelation function') plt.title('Autocorrelation of Noisy Signal') plt.tight_layout() plt.show()運(yùn)行測(cè)試可以得到正確的結(jié)果:Estimated period: 0.02 s
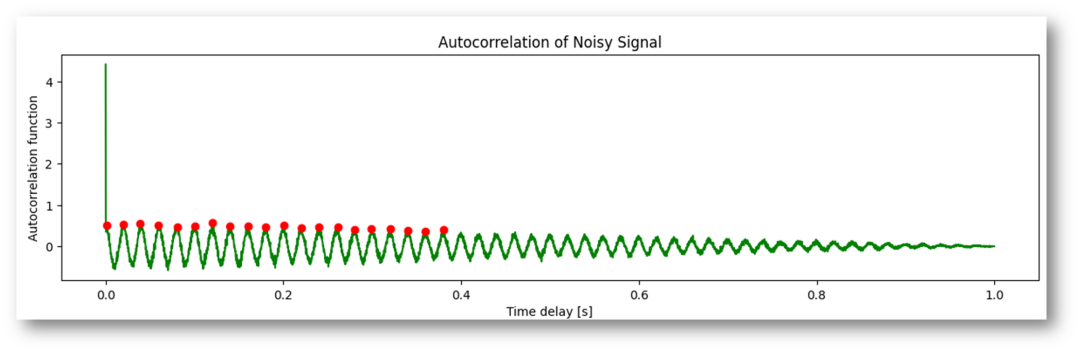
圖-2周期信號(hào)通過相關(guān)性序列的周期檢測(cè)
計(jì)算互相關(guān)函數(shù)需要注意以下幾點(diǎn):
相關(guān)并不表示因果關(guān)系。即使兩變量存在高度相關(guān),也只能表明它們之間存在某種關(guān)系,但并不能確定是哪個(gè)變量影響了另一個(gè)變量。
為了準(zhǔn)確計(jì)算互相關(guān)函數(shù),關(guān)鍵在于靈敏地選擇合適的時(shí)延值。合適的時(shí)延值取決于所考慮系統(tǒng)的特性及其應(yīng)用。
對(duì)于非平穩(wěn)信號(hào)(信號(hào)的統(tǒng)計(jì)特性會(huì)隨著時(shí)間變化),可能需要使用互相關(guān)函數(shù)的改進(jìn)版,如互協(xié)方差函數(shù)等。
需要注意,互相關(guān)函數(shù)對(duì)噪聲非常敏感,信號(hào)的噪聲會(huì)直接影響到相關(guān)運(yùn)算的結(jié)果,因此在進(jìn)行相關(guān)運(yùn)算之前,通常需要對(duì)信號(hào)進(jìn)行去噪處理。
計(jì)算復(fù)雜度高,尤其是數(shù)據(jù)量大的時(shí)候。對(duì)于大數(shù)據(jù)集,可采用快速傅里葉變換(FFT)進(jìn)行降維計(jì)算。FFT算法的時(shí)間復(fù)雜度為O(NlogN),而直接在時(shí)域計(jì)算互相關(guān)函數(shù)的時(shí)間復(fù)雜度則是O(N^2)。
3. 超聲波流量計(jì)中的相關(guān)性原理的應(yīng)用
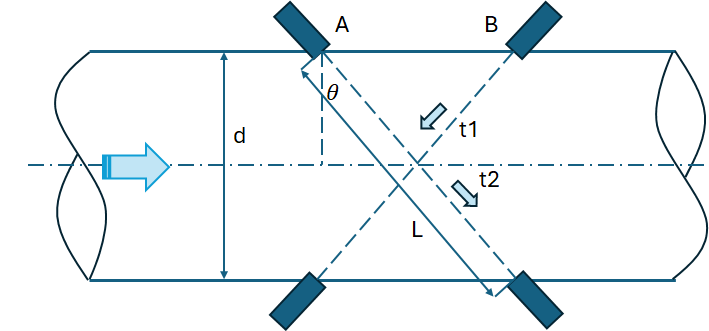
圖-3超聲流量計(jì)的配置圖
要開啟對(duì)超聲流量計(jì)工作原理的討論,關(guān)鍵在于理解超聲波在流體中傳播的特性以及兩者之間如何互動(dòng)。 超聲流量計(jì)采用了所謂的“TOF-時(shí)間飛逝”方法進(jìn)行測(cè)量。超聲收發(fā)的配置會(huì)存在差異。假設(shè)在這種設(shè)備中,有兩對(duì)超聲換能器A和B,按照上圖所示被置于管道的兩側(cè),都是向下發(fā)射,下面的接收。當(dāng)沒有流體流過的時(shí)候,從一個(gè)傳感器發(fā)出的超聲波到達(dá)另一個(gè)傳感器所需的時(shí)間應(yīng)該是恒定的。
然后,當(dāng)流體開始流過時(shí),這個(gè)時(shí)間將會(huì)發(fā)生變化。 超聲波流量計(jì)的構(gòu)造有很多種類,簡(jiǎn)單以上面的圖-3所示。具體來說,當(dāng)流體如圖示的方向流動(dòng)時(shí),從A發(fā)出的超聲波會(huì)被流體帶著一起移動(dòng),所以它到達(dá)接收端的時(shí)間t2會(huì)少于沒有流體流動(dòng)的情況。
反之,從B發(fā)出的超聲波在到達(dá)接收端的過程中需要逆流而上,所以耗費(fèi)的時(shí)間t1會(huì)更多。 在流量計(jì)內(nèi)部,這兩個(gè)時(shí)間被用來計(jì)算出一種稱為“時(shí)間差”的值delay,這就是流體流速的直接度量參數(shù)。根據(jù)這個(gè)delay所對(duì)應(yīng)的時(shí)間來計(jì)算流速的公式見3.2段。 然后,通過對(duì)管道的直徑和流速的測(cè)量,便可以計(jì)算出流量。不過是基于單純TOF時(shí)差的方式,在實(shí)際應(yīng)用中,超聲信號(hào)可能會(huì)受到各種類型噪聲的干擾。
如果信號(hào)受到過多的干擾,將無法正確測(cè)定時(shí)差。為了獲取準(zhǔn)確的流速讀數(shù),我們需要盡量消除這些噪聲帶來的影響。 既然我們看到了相關(guān)性對(duì)于噪聲影響的抵消能力,我們就此引出利用信號(hào)的相關(guān)性進(jìn)行流速測(cè)量的思路方法。本文不是重點(diǎn)于如何設(shè)計(jì),而是提供一種解決問題的思路。
3.1 使用相關(guān)性檢測(cè)相位差法的超聲流量計(jì)的處理大致步驟
超聲波發(fā)射:超聲波流量計(jì)中的超聲換能器發(fā)出的超聲波通常會(huì)以一定的角度,被發(fā)射到流體中。精準(zhǔn)記錄發(fā)射、接收時(shí)間是進(jìn)行相關(guān)性分析的一個(gè)基本要素。
接收信號(hào):流量計(jì)中的兩個(gè)超聲接收器會(huì)分別接收順流和逆流的超聲波信號(hào)。由于流速的原因,這兩個(gè)信號(hào)從各自的發(fā)射到接收之間,會(huì)有一定的時(shí)間差。如果不考慮多普勒頻移,接收到的兩組信號(hào)可以認(rèn)為是同頻及波形相似的。
對(duì)收到的信號(hào)進(jìn)行預(yù)處理:包括但不限于降噪、濾波等。
計(jì)算相關(guān)性:將接收到的兩個(gè)信號(hào)進(jìn)行相關(guān)性計(jì)算,得到相關(guān)函數(shù)。相關(guān)函數(shù)的峰值表示兩個(gè)信號(hào)最相關(guān)(也就是最相似)的位置以及所表示的相位差。
計(jì)算相位差:根據(jù)計(jì)算相關(guān)性序列中得到的對(duì)應(yīng)時(shí)序,得到所代表的兩信號(hào)間在波形上的相位差。而經(jīng)過給定的參數(shù)條件,即可獲取兩組信號(hào)在接收時(shí)的時(shí)間差。
計(jì)算流速:通過已知的聲速,路徑長(zhǎng)度,以及由相位差得到的時(shí)延,本質(zhì)上也是通過計(jì)算TOF的差異,再得到流速。一般可以假定流體為無損耗的流體,流體的湍流程度對(duì)測(cè)量結(jié)果影響可以根據(jù)實(shí)際情況調(diào)整算法。一定要注意:溫度對(duì)于聲速在流體中的影響是明顯的,實(shí)際應(yīng)用中一定要處理好溫度對(duì)于流量計(jì)算的補(bǔ)償。
計(jì)算流量:最后,利用流速和管道斷面積的信息,可以得到流體的體積流量,即通過管道的流體體積與時(shí)間的比值:Q=Av (A為管道橫截面積,v為流速),本文在計(jì)算得到流速后,統(tǒng)一不再計(jì)算流量。
以上就是使用相關(guān)性檢測(cè)相位差法的超聲流量計(jì)的基本處理步驟。需要注意的是,這只是大致步驟,每一步可能會(huì)根據(jù)具體實(shí)現(xiàn),使用的硬件設(shè)備以及信號(hào)處理方法的不同而有所差異。
3.2 使用相關(guān)性檢測(cè)相位差法的超聲流量計(jì)的仿真
依舊參考前面的構(gòu)造圖,并且設(shè)定一些已知條件(比如管徑,流體的聲速—溫度暫不考慮,流速,超聲換能器的安裝角,超聲波的驅(qū)動(dòng)頻率,信號(hào)的采樣頻率等)來看模擬的結(jié)果和給定的已知參數(shù)是否相近或者相等。這里我們以給定的流速和模擬測(cè)量結(jié)果中的流速為比較。
在以下的模擬過程中,兩路信號(hào)各自的生成采集起始時(shí)間是需要盡可能準(zhǔn)確記錄,這樣,我們以其中的一路為信號(hào)為相關(guān)性處理的相對(duì)基準(zhǔn)序列時(shí),在存在流速的情況下,另外一路和該路信號(hào)中間就存在相位差。
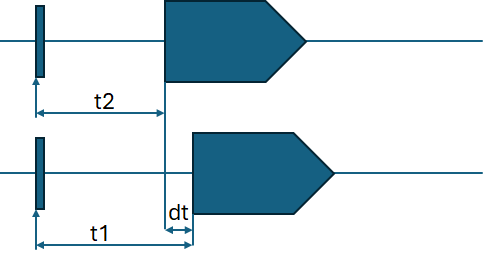
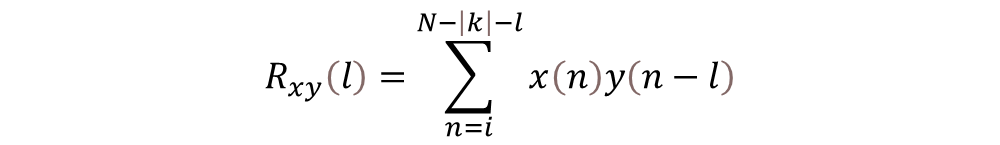
在計(jì)算所得的相關(guān)性序列數(shù)據(jù)中,找到相關(guān)數(shù)值Rxy最大值所對(duì)應(yīng)的時(shí)間“l(fā)”——在波形上是相位——就找到了兩組信號(hào)的相位差,亦即時(shí)間差。以上接收信號(hào)序列中的每個(gè)標(biāo)識(shí),意味著一次數(shù)據(jù)采集的結(jié)果——后文會(huì)提到:數(shù)據(jù)的采樣頻率,也會(huì)影響計(jì)算的精度。
在這里,兩路接收信號(hào)之間的相位差,就是我們要相關(guān)性處理測(cè)量計(jì)算的中間變量。整個(gè)模擬過程中,我們按照之前的分析,暫時(shí)忽略由于流速導(dǎo)致的多普勒頻偏的影響。根據(jù)信號(hào)的相位差得到時(shí)差后,換算成流速的公式如下: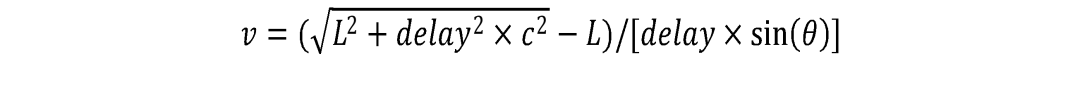
無噪聲情況下的模擬
由以下條件生成的模擬信號(hào),然后看看通過信號(hào)的處理是否可以還原流體的流速。
c = 4500 # 流體中的聲速 m/s
d = 0.5 # 管徑(m)
θ= math.pi / 6 # 超聲換能器的安裝角,30 deg.
L = d / math.cos(theta) # 理想情況下的聲音傳播路徑長(zhǎng)(m)
v = 4 # 流體流速(m/s)-用于生成模擬信號(hào),也是待比較值
f = 1e6 # 超聲波的驅(qū)動(dòng)頻率 1MHz
T = 1 / f # 驅(qū)動(dòng)頻率的周期時(shí)間(s)
Fs = 125e6 # 采樣頻率為125MHz
Ts = 1/Fs # 采樣間隔
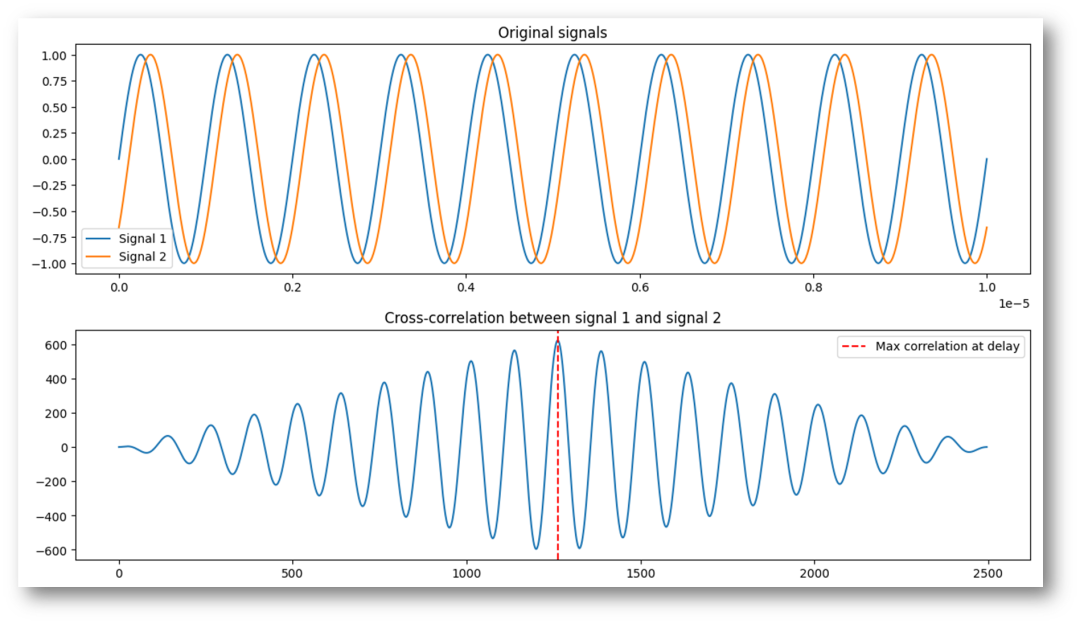
圖-4無噪聲正弦信號(hào)的相關(guān)性檢測(cè)
仿真的結(jié)果如下:
Length of t lags: 2497
Length of t serial: 1249
Ts Delayed cycles: 14
Delayed time: 1.1208967173738991e-07s
shift degree: 40.352281825460366
Sample time interval: 8.00640512409928e-09s
Estimated velocity: 3.9314356314212877(m/s)
可以看到,通過模擬信號(hào)進(jìn)行相關(guān)性處理之后得到的流體速度計(jì)算結(jié)果,和模擬信號(hào)中設(shè)定的“實(shí)際”流速很接近,僅1.71%的誤差。
如果接收信號(hào)的幅值不一樣會(huì)有什么影響?我們來模擬一下:兩個(gè)超聲換能器接收到的信號(hào)乃至放大之后采集到的信號(hào)仍然存在不一致時(shí),對(duì)測(cè)量結(jié)果是否會(huì)有影響?
下圖中信號(hào)#2的幅值已經(jīng)是信號(hào)#1幅值的2倍了。
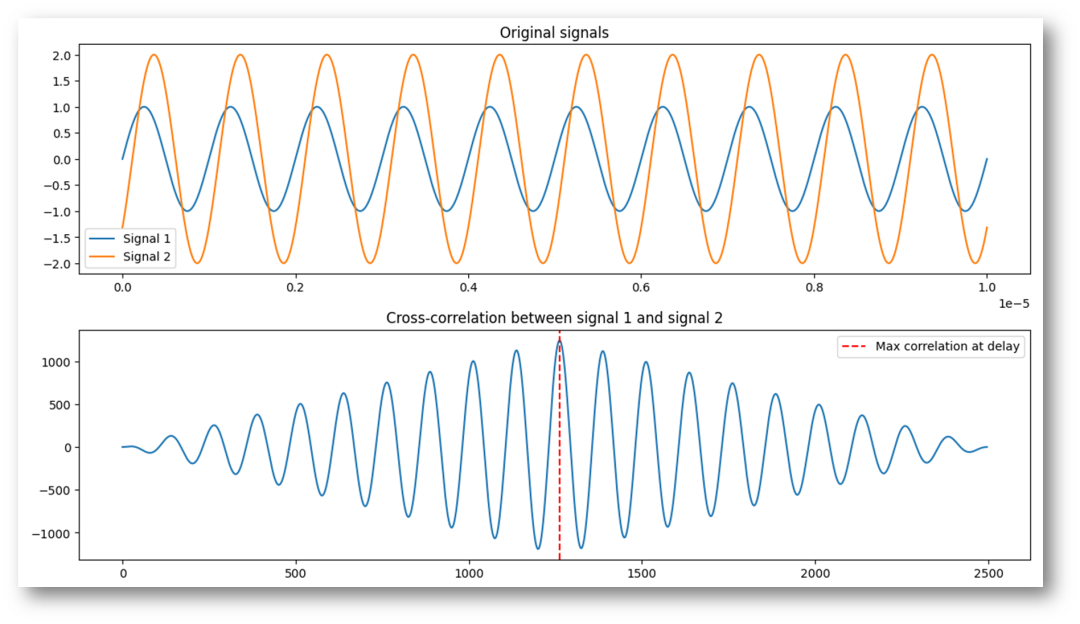
圖-5幅值不同的兩個(gè)正弦信號(hào)的相關(guān)性檢測(cè)
我們看到,接收信號(hào)的幅值不一樣的情況下,測(cè)量所得的流速和前面信號(hào)同幅值時(shí)是一樣的。可見理想情況下,幅值對(duì)測(cè)量值影響不是首位的,但是實(shí)際應(yīng)用中肯定存在噪聲,而有噪聲我們就需要強(qiáng)調(diào)信噪比,因此雖然模擬結(jié)果尚可,但是信號(hào)的有效幅值我們還是希望更高些。
Estimated velocity: 3.9314356314212877(m/s)
有噪聲情況下的模擬
信噪比是隨便選的,但是我們可以看到在有噪聲的影響下,單純使用時(shí)差檢測(cè)的方法將無法再檢測(cè)時(shí),通過信號(hào)序列的相關(guān)性處理,仍然可以有相應(yīng)的輸出。我們將兩路信號(hào)加上各自幅值的0.5倍的隨機(jī)噪聲。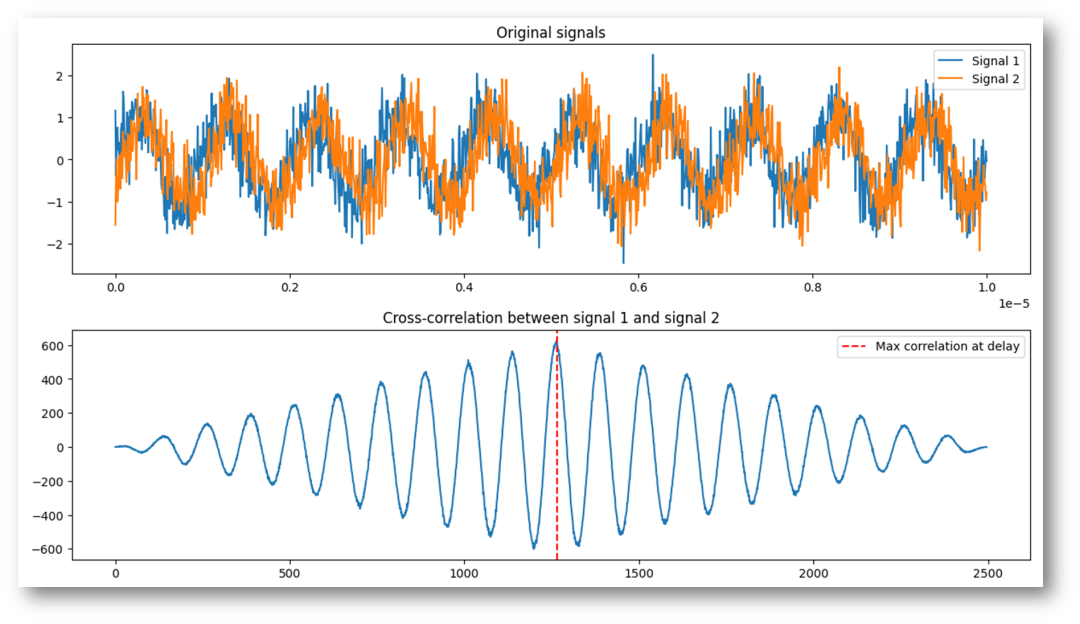
圖-6帶加性噪聲的兩個(gè)正弦信號(hào)的相關(guān)性檢測(cè)
雖然可以檢測(cè),但是此時(shí)得到的結(jié)果是4.77m/s,和理想模擬值流速=4m/s有了較大差異。
Length of t lags: 2497
Length of t serial: 1249
Ts Delayed cycles: 17
Delayed time: 1.3610888710968775e-07
degree: 48.9991993594876
Sample time interval: 8.00640512409928e-09
Estimated velocity: 4.773885690505651(m/s)
可見,噪聲將影響測(cè)量的精度。如果我們?cè)谠O(shè)計(jì)硬件過程中,已經(jīng)充分考慮了信號(hào)的收發(fā)部分的濾波處理,也將非常有利于最后測(cè)量值的精度和穩(wěn)定性。關(guān)于信號(hào)濾波這部分,在稍后也需要用到。
以下是上面模擬有、無噪聲信號(hào)處理所用的python代碼,僅供參考。代碼中在生成的信號(hào)中添加了隨機(jī)噪聲,不需要時(shí)請(qǐng)注釋掉。
import numpy as np import matplotlib.pyplot as plt from scipy.signal import correlate import math def cor_demo(): try: # Parameters c = 4500 # Sound speed in the fluid in m/s d = 0.5 # Pipe diameter in meters theta = math.pi / 6 # Angle of the emitted ultrasound wave, in radians. 30 degrees here. L = d / math.cos(theta) # The sound path length in meters parallel to the flow direction v = 4 # Fluid velocity in m/s f = 1e6 # Frequency of the signal in 1MHz T = 1 / f # Period of the signal in s Fs = 125e6 # 采樣頻率為125MHz Ts = 1/Fs # 采樣間隔 # Calculate time delay caused by flow velocity time_up = L / (c - v * math.sin(theta)) # Time of flight upstream time_down = L / (c + v * math.sin(theta)) # Time of flight downstream #t_delay = L / c * (1 / np.sqrt(1 - (v / c * np.sin(theta)) ** 2) - 1) print("T1_0:",time_up-time_down) t_delay = 2 * L * v * np.sin(theta) / (c**2 - v**2 * np.sin(theta)**2) # Time array # 返回一個(gè)從0到period*T范圍內(nèi)的有num_samples個(gè)元素的一維數(shù)組,數(shù)組中的數(shù)值是等間距分布的 period = 10 num_samples = period*T/Ts t = np.linspace(0, period*T, int(num_samples)) # Signals s0 = np.sin(2 * np.pi * f * t) s1 = np.sin(2 * np.pi * f * (t - t_delay)) #*2.0 # Signal 1 #=====添加噪聲:mask this seg to remove noise from signals========= noise0 = np.random.normal(0, 0.5, s0.shape) noise1 = np.random.normal(0, 0.5, s1.shape) s0 = s0 + noise0 s1 = s1 + noise1 #=====mask the seg above to remove noise from signals========= # 計(jì)算Cross-correlation,并找到最大值對(duì)應(yīng)的位置 correlation = correlate(s1, s0, method='direct', mode='full') lags = np.arange(-len(s1) + 1, len(s1)) # Lags array print("Length of t lags:", len(lags)) # Calculate flow speed using the estimated time delay # Find the peak of the cross-correlation corresponds to the time delay print("Length of t serial:", len(t)) delay = lags[np.argmax(correlation)] # 相位差所對(duì)應(yīng)的信號(hào)序列值 sample_time = (period*T) / len(t) # 采樣間隔時(shí)間 time_delay = delay * sample_time # 兩個(gè)信號(hào)間的延遲時(shí)間 phase_shift = (time_delay / T) * 2 * np.pi # 由時(shí)間延遲換算成的兩個(gè)信號(hào)序列的相位差 phase_shift_deg = phase_shift * (180 / np.pi) # 由相位差換成的兩個(gè)信號(hào)序列的角度差 print("Ts Delayed cycles:", delay, ", Delayed time: ", time_delay, "degree:", phase_shift_deg) # 將延遲轉(zhuǎn)換為相位差 print("Sample time interval:",sample_time) # 計(jì)算所得的流速 v_estimated = (math.sqrt((L**2)+(time_delay**2)*(c**2))-L)/(time_delay * math.sin(theta)) print('Estimated velocity: ', v_estimated) # 畫圖 #fig, (ax_origin, ax_corr, ax_shift) = plt.subplots(2, 1, figsize=(12, 8)) fig, (ax_origin, ax_corr) = plt.subplots(2, 1, figsize=(12, 8)) # 原始信號(hào)圖 ax_origin.plot(t, s0, label='Signal 1') ax_origin.plot(t, s1, label='Signal 2') ax_origin.set_title('Original signals') ax_origin.legend() # 互相關(guān)圖 ax_corr.plot(correlation) ax_corr.axvline(x = len(correlation)//2 + delay, color = 'r', linestyle = '--', label = "Max correlation at delay") ax_corr.set_title('Cross-correlation between signal 1 and signal 2') ax_corr.legend() plt.tight_layout() plt.show() return except Exception as e: print("Error:",e) if __name__=='__main__': cor_demo()4.超聲波流量計(jì)中的信號(hào)相關(guān)性處理中的插值處理
需要了解的是,在信號(hào)采集過程中,足夠快的采樣率是保證相位差有足夠分辨率的保證。對(duì)應(yīng)的是模擬代碼中“Ts Delayed cycles”。容易設(shè)想,如果我們可以在處理器足夠快的前提下,還可以得到更多的“Ts Delayed cycles”,就意味著相位差的分辨率就可以足夠高。
在上面的模擬過程中,DAQ的采樣頻率是125MHz,對(duì)應(yīng)一些高速ADC器件。反之呢?如果實(shí)際使用的ADC器件的采樣率因?yàn)槟承┰蛩俣炔⒉皇悄敲锤邥r(shí),我們的模擬結(jié)果會(huì)出現(xiàn)什么情況?
下面的波形是將ADC的采樣頻率調(diào)整為12.5MHz時(shí)的輸出。
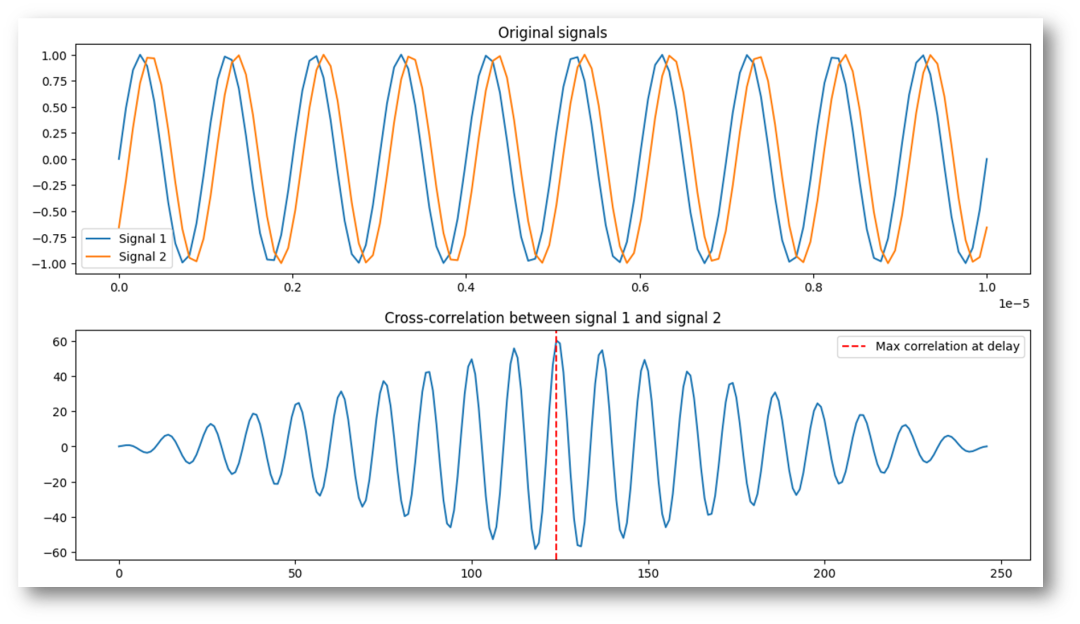
圖-7降低信號(hào)采集頻率后的相關(guān)性檢測(cè)
采集到的波形來看,正弦波已經(jīng)有點(diǎn)異常了。從模擬結(jié)果來看,即使是其他都是理想的情況下,流速結(jié)果和4m/s的設(shè)定相差就很多了。
Estimated velocity: 2.828550434230693(m/s)——插值前
在這種情況下,有無其他的方式提高最后輸出結(jié)果的精度?答案是肯定的,那就是插值——我們已經(jīng)設(shè)定這個(gè)波形是近正余弦的,在python中,我們看到軟件包scipy有3階樣條插值的實(shí)現(xiàn)方式函數(shù):scipy.interpolate.interp1d。以下的仿真結(jié)果就是基于該插值方式實(shí)現(xiàn)的。 插值的過程,就是在已有的時(shí)間序列中,每個(gè)間隔之間均勻地插入設(shè)定的時(shí)間點(diǎn)數(shù),然后通過插值函數(shù),在已采集的信號(hào)(這里是模擬的采集信號(hào))中,對(duì)應(yīng)插入的時(shí)間點(diǎn)上,使用3階樣條插值,添加額外的插值。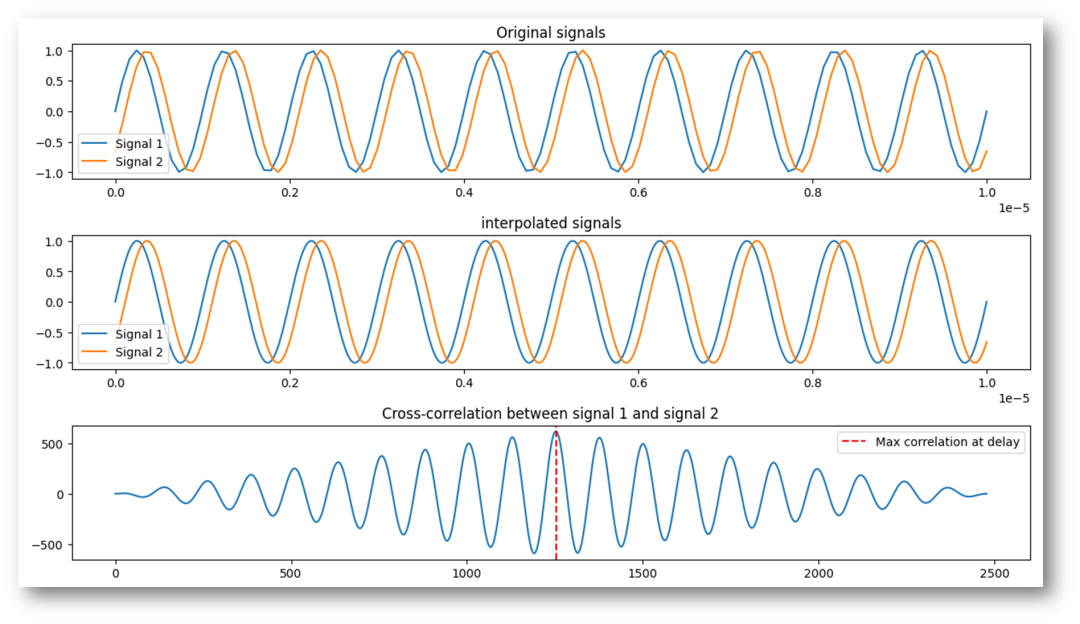
圖-8插值法提高相關(guān)性檢測(cè)精度的輸出
上圖是通過插值方法得到的輸出圖。第一個(gè)圖,是沒有插值時(shí)的2路信號(hào)輸出圖,該圖和前一個(gè)圖中的信號(hào)波形是一致的,都是基于12.5MHz的采樣率生成的。第二個(gè)圖和第三個(gè)圖,就是在12.5MHz采樣率的采集信號(hào)的前提下插值得到的。這里每?jī)蓚€(gè)源數(shù)據(jù)之間插入點(diǎn)數(shù)有10個(gè),實(shí)際應(yīng)用過程中,應(yīng)該需要充分考慮處理器的處理速度,流量測(cè)量的實(shí)時(shí)性要求。
Estimated velocity: 3.959970232994945m/s——插值后 得到的模擬流速測(cè)量結(jié)果也是很接近設(shè)定的模擬流速(4m/s)的。并且,其中的數(shù)據(jù)點(diǎn),有原先的247個(gè),經(jīng)過插值后,達(dá)到2479個(gè),相對(duì)于增加了分辨率。
需要特別提出,信號(hào)的完整性在這里是重要的,濾波!否則插值的結(jié)果也將是亂七八糟的。如下圖,直接在噪聲疊加的信號(hào)上進(jìn)行插值。模擬結(jié)果也測(cè)試了,不盡如人意,和設(shè)定值相差較大。大家可以用本文附帶的代碼進(jìn)行驗(yàn)證測(cè)試一下。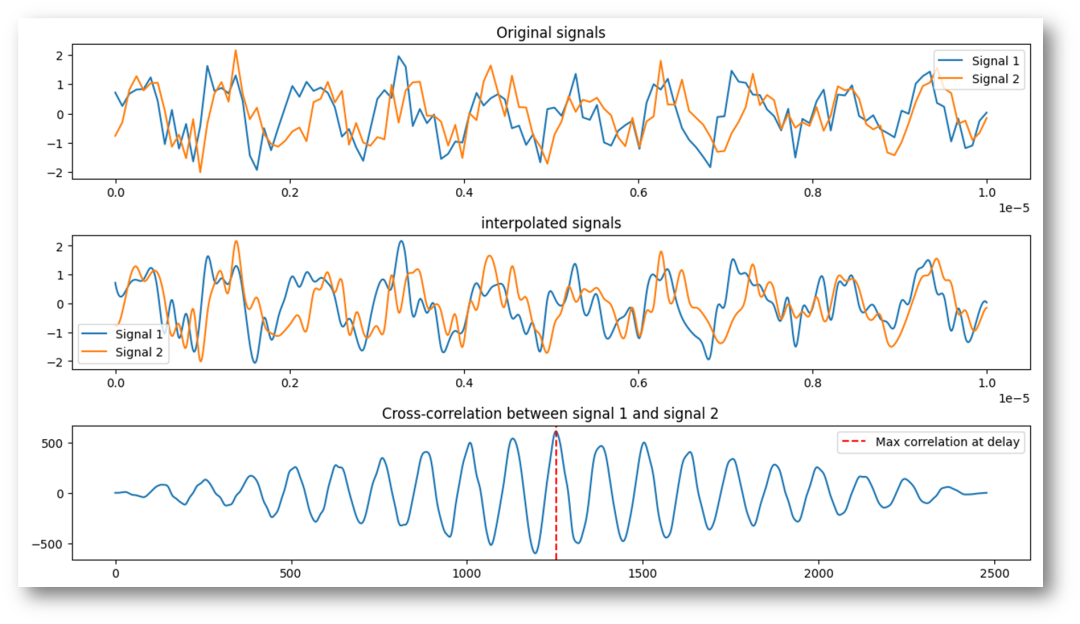
圖-9帶噪聲未濾波情況下的插值后相關(guān)性檢測(cè)輸出
插值運(yùn)算相位差和流速。下面是模擬代碼,僅供參考。以下代碼中,噪聲部分是注釋掉的。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate
import math
from scipy.interpolate import interp1d
def cor_demo():
try:
# Parameters
c = 4500 # Sound speed in the fluid in m/s
d = 0.5 # Pipe diameter in meters
theta = math.pi / 6 # Angle of the emitted ultrasound wave, in radians. 30 degrees here.
L = d / math.cos(theta) # The sound path length in meters parallel to the flow direction
v = 4 # Fluid velocity in m/s
f = 1e6 # Frequency of the signal in 1MHz
T = 1 / f # Period of the signal in s
Fs = 125e5 # 采樣頻率為12.5MHz
Ts = 1/Fs # 采樣間隔
# Calculate time delay caused by flow velocity
time_up = L / (c - v * math.sin(theta)) # Time of flight upstream
time_down = L / (c + v * math.sin(theta)) # Time of flight downstream
#t_delay = L / c * (1 / np.sqrt(1 - (v / c * np.sin(theta)) ** 2) - 1)
print("T1_0:",time_up-time_down)
t_delay = 2 * L * v * np.sin(theta) / (c**2 - v**2 * np.sin(theta)**2)
# Time array
# 返回一個(gè)從0到period*T范圍內(nèi)的有num_samples個(gè)元素的一維數(shù)組,數(shù)組中的數(shù)值是等間距分布的
period = 10
num_samples = period*T/Ts
t = np.linspace(0, period*T, int(num_samples))
# Signals
s0 = np.sin(2 * np.pi * f * t)
s1 = np.sin(2 * np.pi * f * (t - t_delay)) #*2.0 # Signal 1
"""
noise0 = np.random.normal(0, 0.5, s0.shape)
noise1 = np.random.normal(0, 0.5, s1.shape)
s0 = s0 + noise0
s1 = s1 + noise1
"""
# Define interpolation factor
interp_factor = 10
# New time vector after interpolation
t_new = np.linspace(t.min(), t.max(), t.size * interp_factor)
# Create a function based on the original signals, which can be used to generate the interpolated signals
interp_func_s0 = interp1d(t, s0, kind='cubic')
interp_func_s1 = interp1d(t, s1, kind='cubic')
# Generate the interpolated signals
s0_new = interp_func_s0(t_new)
s1_new = interp_func_s1(t_new)
# 計(jì)算Cross-correlation,并找到最大值對(duì)應(yīng)的位置
#correlation = correlate(s1, s0, method='direct', mode='full') # old
correlation = correlate(s1_new, s0_new, method='direct', mode='full')
lags = np.arange(-len(s1_new) + 1, len(s1_new)) # Lags array
print("Length of t lags:", len(lags))
# Calculate flow speed using the estimated time delay
# Find the peak of the cross-correlation corresponds to the time delay
#print("Length of t serial:", len(t))
delay = lags[np.argmax(correlation)] # 相位差所對(duì)應(yīng)的信號(hào)序列值
#sample_time = (period*T) / len(t) # 采樣間隔時(shí)間 old
sample_time = (period*T) / len(t_new)
time_delay = delay * sample_time # 兩個(gè)信號(hào)間的延遲時(shí)間
phase_shift = (time_delay / T) * 2 * np.pi # 由時(shí)間延遲換算成的兩個(gè)信號(hào)序列的相位差
phase_shift_deg = phase_shift * (180 / np.pi) # 由相位差換成的兩個(gè)信號(hào)序列的角度差
print("Ts Delayed cycles:", delay, ", Delayed time: ", time_delay, "degree:", phase_shift_deg) # 將延遲轉(zhuǎn)換為相位差
print("Sample time interval:",sample_time)
# 計(jì)算所得的流速
v_estimated = (math.sqrt((L**2)+(time_delay**2)*(c**2))-L)/(time_delay * math.sin(theta))
print('Estimated velocity: ', v_estimated)
# 畫圖
#fig, (ax_origin, ax_corr, ax_shift) = plt.subplots(2, 1, figsize=(12, 8))
fig, (ax_origin, ax_interpo, ax_corr) = plt.subplots(3, 1, figsize=(12, 8))
# 原始信號(hào)圖
ax_origin.plot(t, s0, label='Signal 1')
ax_origin.plot(t, s1, label='Signal 2')
ax_origin.set_title('Original signals')
ax_origin.legend()
# 插值后的信號(hào)圖
ax_interpo.plot(t_new, s0_new, label='Signal 1')
ax_interpo.plot(t_new, s1_new, label='Signal 2')
ax_interpo.set_title('interpolated signals')
ax_interpo.legend()
# 互相關(guān)圖
ax_corr.plot(correlation)
ax_corr.axvline(x = len(correlation)//2 + delay, color = 'r', linestyle = '--', label = "Max correlation at delay")
ax_corr.set_title('Cross-correlation between signal 1 and signal 2')
ax_corr.legend()
plt.tight_layout()
plt.show()
return
except Exception as e:
print("Error:",e)
if __name__=='__main__':
cor_demo()
另外一個(gè)大家可以嘗試比較的是:根據(jù)奈奎斯特采樣定理,信號(hào)的采集頻率至少應(yīng)該是被采集信號(hào)帶寬的2倍以上,才可以從采集信號(hào)中回復(fù)原信號(hào)。是不是還可以再降低一些采樣頻率然后通過插值的方式來提高測(cè)量精度呢?
5.小結(jié)
本文中提高的模擬信號(hào)及分析方式僅供理論參考,實(shí)際的超聲接收信號(hào)不會(huì)是圖示中的那樣都是完美的正余弦波形。
超聲流量計(jì)通過利用超聲波在流體中傳播的特性來測(cè)量流量,其中使用相位差方式是一種常見的方法。它的特點(diǎn)主要包括:
非接觸測(cè)量:通過在管道外壁上安裝超聲探頭,可以避免對(duì)流體產(chǎn)生任何影響,適合處理易激發(fā)、高溫或腐蝕性的流體。
較高精度:相位差法可以實(shí)現(xiàn)較高的測(cè)量精度,因?yàn)樗苯訙y(cè)量的是流體的流動(dòng)速度,而非其他的,可能受到流體性質(zhì)變化影響的參數(shù)。
廣泛適用:適用于各種類型的流體,包括氣體、液體和蒸汽,并且管道大小范圍廣泛。
然而,在使用超聲流量計(jì)時(shí),我們需要注意以下可能影響測(cè)量精度的問題:
流體的溫度、壓力和流速狀態(tài)變化:這些因素可能影響超聲波在流體中的傳播速度,從而影響測(cè)量結(jié)果,尤其是溫度對(duì)于超聲波在液體中的傳播速度的影響。
超聲探頭的安裝位置和角度:如果探頭的安裝位置或角度不準(zhǔn)確,會(huì)導(dǎo)致超聲波不能正確地穿過流體,影響測(cè)量結(jié)果。
管道和流體的不同:如果流體的性質(zhì)(如粘度、密度)或者管道的材料和狀況發(fā)生變化,可能需要重新校準(zhǔn)設(shè)備。
流體中的顆粒或氣泡:這些可能會(huì)吸收、散射或者反射超聲波,從而影響信號(hào)質(zhì)量。
以上并未考慮由于流速引起的多普勒頻移影響。
以上都是在使用超聲流量計(jì)時(shí)應(yīng)注意的問題,以確保測(cè)量的準(zhǔn)確性。
審核編輯:劉清
-
流量傳感器
+關(guān)注
關(guān)注
1文章
180瀏覽量
22132 -
無線通信
+關(guān)注
關(guān)注
58文章
4519瀏覽量
143413 -
信噪比
+關(guān)注
關(guān)注
3文章
253瀏覽量
28591 -
超聲流量計(jì)
+關(guān)注
關(guān)注
0文章
10瀏覽量
6896
原文標(biāo)題:流量傳感器(2)超聲流量傳感器—相位差和信號(hào)相關(guān)性原理
文章出處:【微信號(hào):安費(fèi)諾傳感器學(xué)堂,微信公眾號(hào):安費(fèi)諾傳感器學(xué)堂】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
相位差測(cè)量與虛擬相位差計(jì)
使用相關(guān)性測(cè)量相位差
對(duì)于電容、電感產(chǎn)生的相位差該如何理解
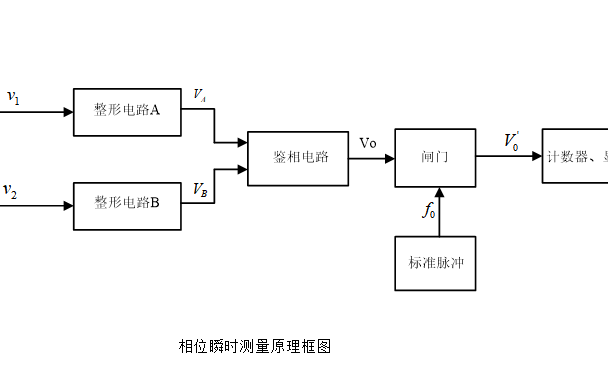
簡(jiǎn)易數(shù)顯式工頻信號(hào)相位差測(cè)量?jī)x的詳細(xì)資料說明
詳解電容、電感的相位差是如何產(chǎn)生的
發(fā)射信號(hào)與接收信號(hào)之間的相位差如何計(jì)算
如何理解電容、電感產(chǎn)生的相位差
RC電路中相位差是如何引起的?電路中的相位差與哪些因素有關(guān)?
如何減小電流互感器的相位差
移相電路引起相位差的原因是什么
使用泰克示波器觀察相位差





 超聲流量傳感器—相位差和信號(hào)相關(guān)性原理解析
超聲流量傳感器—相位差和信號(hào)相關(guān)性原理解析











評(píng)論