圖機器學習(Graph Machine Learning,簡稱Graph ML)是機器學習的一個分支,專注于利用圖形結構的數據。在圖形結構中,數據以圖的形式表示,其中的節點(或頂點)表示實體,邊(或鏈接)表示實體之間的關系。
本篇文章將從基礎開始介紹什么是圖,我們如何描述和表示它們,以及它們的屬性是什么。
圖論是在18世紀由歐拉引入的,用來解決著名的柯尼斯堡大橋問題:是否有可能只穿過七座橋中的每座橋一次。

什么是圖?如何定義它?
圖就是一組相互連接的對象。
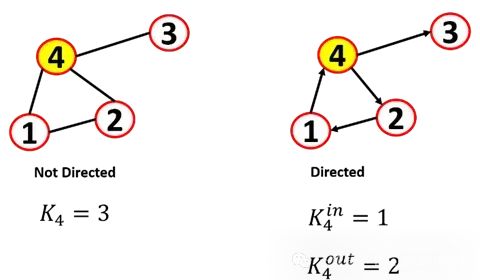
一個圖有一組結點N和邊E, n是頂點的數目,m是邊的數目。連接的兩個節點被定義為相鄰(節點1相鄰或鄰接4)。當我們稱網絡的大小N時,通常指的是節點的數量(鏈路或邊的數量通常稱為L)。

有向與無向
圖可以是無向圖或有向圖:
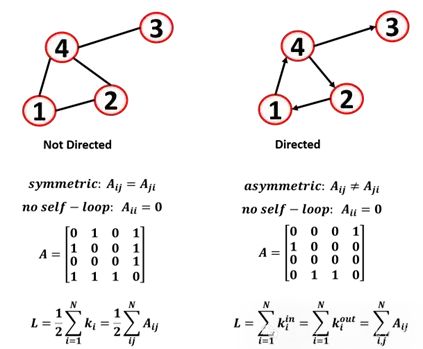
無向圖:邊是無向的,關系是對稱的。畫邊的順序并不重要。
有向圖:邊是有向的(也稱為有向圖),頂點之間的邊可以有方向,可以用箭頭表示(也稱為弧線)。
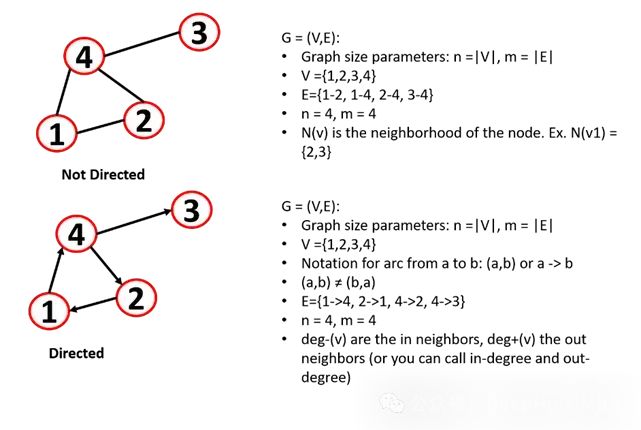
圖的基本性質
對于一個節點,我們可以將節點度(k)定義為與節點相鄰的邊,對于一個圖,我們可以計算無向圖的平均度k:
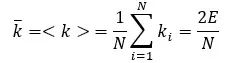
在有向網絡中,定義了一個節點的入度(指指向該節點的邊)和出度(指離開該節點的邊),節點的總度是兩者的和。我們稱source節點為沒有入度的節點,稱sink節點為沒有出度的節點。
我們可以計算平均度為:
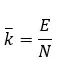
這里的
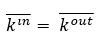
鄰接矩陣是表示圖的另一種方式,其中行和列表示圖節點,交集表示一個節點的兩個節點之間是否存在鏈接。鄰接矩陣的大小是n x n(頂點數)。如果Aij是節點i和j之間的鏈接,則Aij為1,否則為0,對于無向圖,矩陣是對稱的。可以看到在矩陣的對角線上沒有1意味著沒有自環(節點與自身相連)

對于一個節點 i 計算一個節點的邊(或它的度),沿著行或列求和:
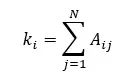
無向圖中的總邊數是每個節點的度之和(也可以是鄰接矩陣中的值之和):
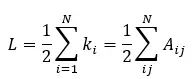
因為在無向圖中,你要計算兩次邊(由于鄰接矩陣是對稱的,要計算兩次相同的邊),所以除以2
對于有向圖,可以表示兩個不同的鄰接矩陣,一個表示入度,一個表示出度

對于一個節點,總邊數是入度和出度之和:
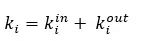
我們計算一個節點的入度和出度以及總邊數:
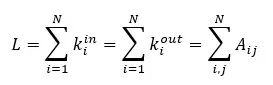
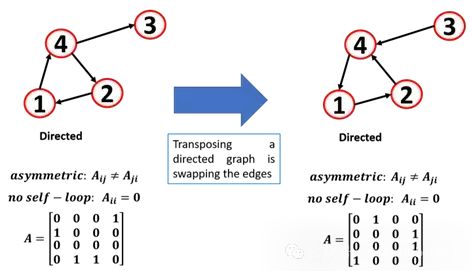
由于線性代數和圖論之間存在聯系,所以可以對鄰接矩陣應用不同的操作。如果轉置一個無向圖的鄰接矩陣,圖是沒有改變的因為是對稱的,但如果轉置一個有向圖的鄰接矩陣,邊則進行了方向的轉換。
這些矩陣非常是稀疏的,因為理論上一個節點是可以連接到所有其他節點,但這在現實生活中基本上不會發生。當所有節點都與其他節點相連時,我們稱之為完全圖。完全圖通常用于理解圖論中的一些復雜問題(連通性例子等)。
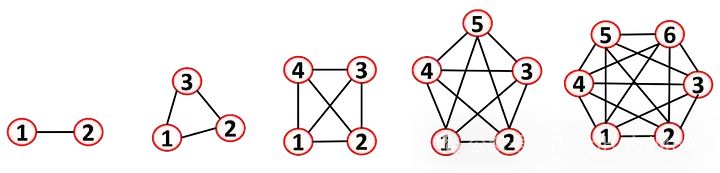
圖的最大密度是一個完全圖中可能關系的總數。實際密度是測量無向非完全圖的密度:
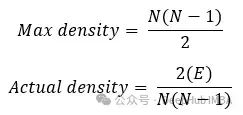
理論上來說在社交網絡中,每個人都可以連接到每個人,但這并沒有發生。所以最終得到一個 70 億行和 70 億列的鄰接矩陣,其中大多數條目為零(因為非常稀疏)。為什么要說這個呢?因為不是所有的算法都能很好地處理稀疏矩陣。
除了鄰接矩陣,我們還可以將圖表示為一個邊的列表:
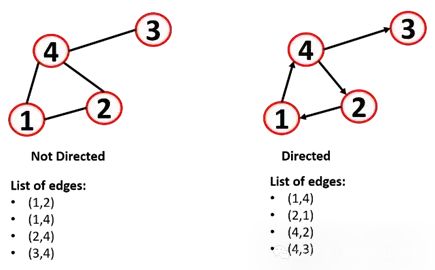
但是這種方法對于機器學習分析是有問題的,所以就出現了一種常用的方法:鄰接表,因為鄰接表對大型和稀疏的節點很有用,它允許快速檢索節點的鄰居。
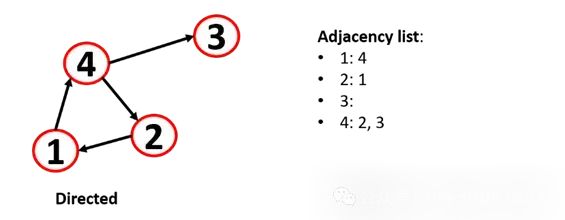
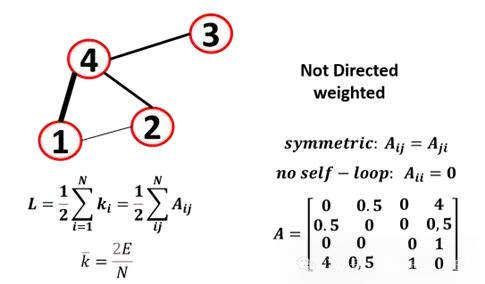
加權圖
圖邊還可以增加權值,邊并不都是相同的,比如在交通圖中,為了選擇兩個節點之間的最佳路徑,我們將考慮表示時間或交通的權重。
自循環
圖的節點是可以連接到自己的,所以必須在計算總邊數時添加自循環
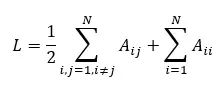
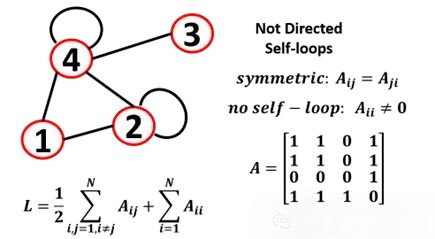
你也可以有一個多圖,一個對節點有多條邊
多重圖
含有平行邊的圖稱為多重圖,或者說一個對節點有多條邊
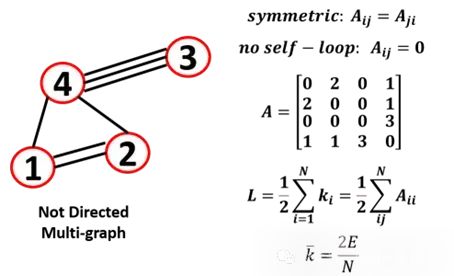
上面就是一些常見的圖和表示方式,我們來做一個匯總
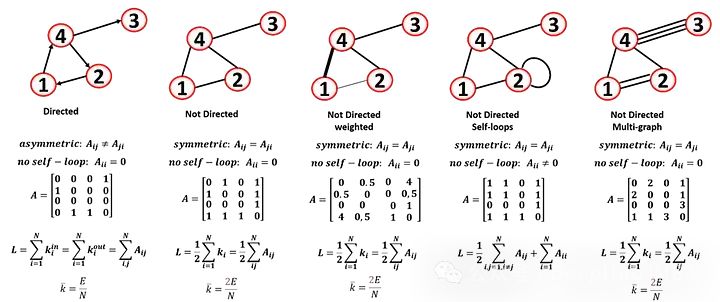
圖的另一個重要參數是連接性(連通性)。每個節點都能被所有其他節點到達嗎?連通圖是指所有頂點都可以通過一條路徑連接起來的圖。不連通圖是指有兩個或多個連通分量的圖
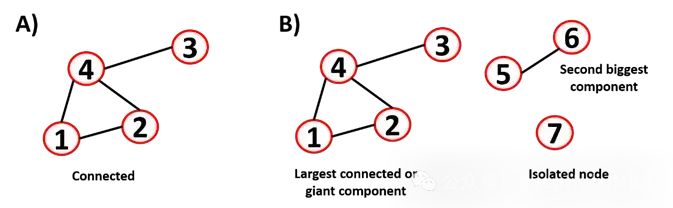
最大的隔離的節點子集被稱為“孤島”(island)。知道圖是連通的還是不連通的是很重要的,有些算法很難處理不連通的圖。
這可以在鄰接矩陣中顯示,其中不同的組件被寫成對角線塊(非零元素被限制在平方矩陣中)。我們稱連接兩個“孤島”的鏈接“橋”(bridge)
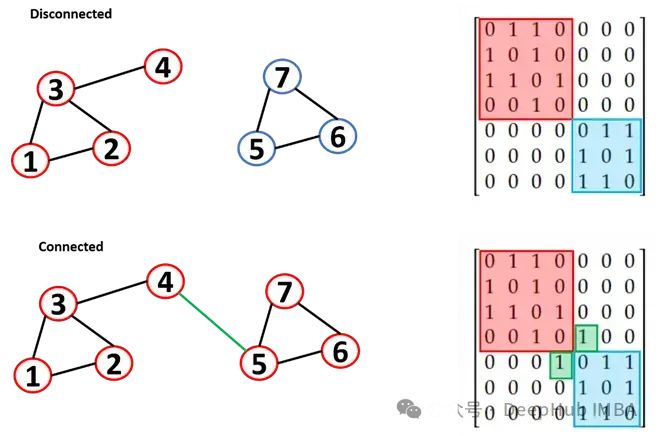
如果圖很小,這種視覺檢查很容易,但對于一個大圖,檢查連通性是非常有挑戰的。
雙部圖
我們上面所看到的圖稱為單部圖,其中只有一種類型的節點和一種類型的關系
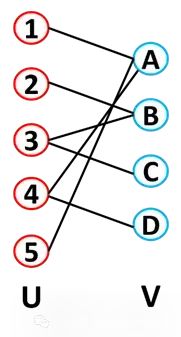
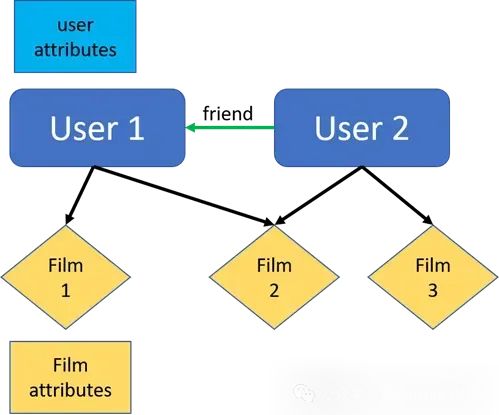
雙部圖是一種將節點劃分為兩個不相交集合(通常稱為 U 和 V)的圖。這些集合是獨立的,U 集合中的每個節點都與 V 集合中的某個節點相連(每個鏈接只能連接一個集合中的節點到另一個集合中的節點)。因此,雙部圖是一種不存在 U-U 連接和 V-V 連接的圖。有許多這樣的例子:作者到論文(作者位于 U 集合,并且他們與他們撰寫的論文即 V 集合相連)、演員(U)和他們參演的電影(V)、用戶和產品、食譜和配料等。另一個例子是疾病網絡,其中包括一組疾病和一組基因,只有包含已知會導致或影響該疾病的突變的基因才與該疾病相連。另一個例子是匹配,雙部圖可用于約會應用程序。對于一個有兩組節點的雙部圖(U 有 m 個節點,V 有 n 個節點),可能的邊的總數是 m*n,節點的總數是 m + n。
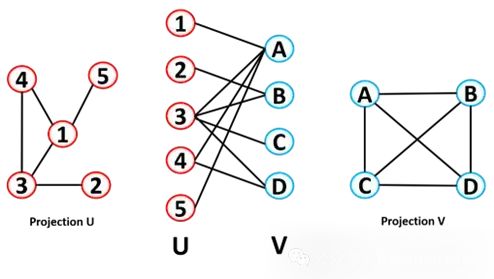
雙部圖可以折疊成兩個單獨的網絡,U 的投影和 V 的投影。在 U 的投影中,如果兩個節點連接到同一個 V 節點,則它們相連(V 投影的原理相同)。
如果需要,我們也可以構建一個三部圖。總的來說,你可以擁有超過三種類型的節點,通常我們講的是 k-部圖。這種類型的圖擴展了我們對雙部圖的看法。
異構圖
異構圖(也稱異質圖)是一種具有不同類型的節點和邊的圖。
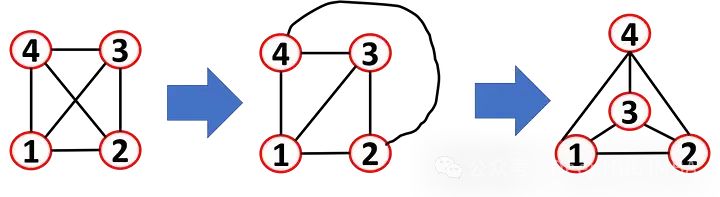
平面圖
如果一幅圖可以繪制成沒有任何邊相交的形式(對于圖來說,如果可以以這種方式繪制,它被稱為平面表示),則可以將其視為平面圖。即使繪制時邊相交,圖也可以是平面的。看這個例子,這幅圖可以重新繪制成平面表示。
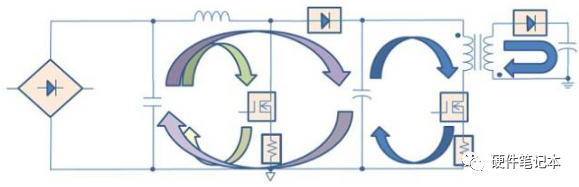
為什么知道我們是否可以有平面表示很有用?最常用的一個例子是繪制電路版,要保證電路不會相交。
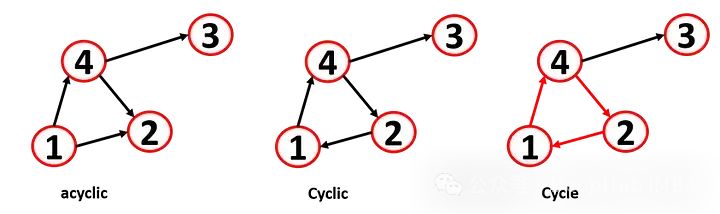
循環圖與非循環圖
線路 (walk) 是節點的交替序列(u-v 的線路是從 u 開始并在 v 結束的節點序列)。路徑(path)是序列中節點各不相同的線路(u-x-v 是一條路徑,但 u-x-u-x-v 是線路但不是路徑)。循環圖是路徑開始和結束于同一節點的圖,因為不同的算法都有循環問題(所以有時需要通過切斷一些連接將循環圖轉換為非循環圖)。我們可以將前饋神經網絡定義為有向無環圖(DAG),因為DAG 總是有一個結束點(也稱為葉子節點)。
總結
在本文中,我們介紹了什么是圖及其主要屬性,盡管圖看起來很簡單,但可以實現無限的變化。圖是節點和邊的集合;它沒有順序,沒有開始也沒有結束。我們可以通過它們定義不同類型的概念和數據。圖還可以簡潔地描述數據的許多屬性,并為我們提供關于不同主題之間關系的信息。例如,我們可以為節點和邊分配權重和屬性。在以后的文章中,我們將討論如何在這些網絡中使用算法(以及如何表示它們)。
作者:Salvatore Raieli
來源:DeepHub IMBA
-
AI
+關注
關注
87文章
30239瀏覽量
268475 -
人工智能
+關注
關注
1791文章
46896瀏覽量
237666 -
機器學習
+關注
關注
66文章
8382瀏覽量
132441
發布評論請先 登錄
相關推薦
X電容和Y電容的基本概念
AI入門之深度學習:基本概念篇

BP網絡的基本概念和訓練原理
卷積神經網絡的基本概念、原理及特點
機器學習中的數據預處理與特征工程
遷移學習的基本概念和實現方法
循環神經網絡的基本概念
組合邏輯控制器的基本概念、實現原理及設計方法
萬用表的基本概念及結構組成
電源路徑的基本概念




 圖機器學習入門:基本概念介紹
圖機器學習入門:基本概念介紹













評論