在之前我們的博文中,所提到的數據的濾波處理和仿真分析,其實都是圍著一段固定長度的模擬數據展開的,除了知道濾波器的幅頻、相頻響應特性之外,也直觀地看到了濾波的效果會是怎么樣的。實際應用會怎么樣?需要怎么處理?
假設需要對音頻,視頻,或者儲存的大量數據等進行處理時,期待全部讀取然后一次處理顯然是不合適,也沒有必要,而且資源和實時性都無法滿足。而分段處理,需要的資源少是一方面,并行和分布處理難道不考慮一下?
那分段處理,能否將每段濾波之后獲取的數據直接拼接作為整體濾波后的數據呢?然而分段處理需要考慮有其特殊性。
就信號處理而言,FIR系統和IIR系統的處理方式各有特點。
IIR系統的連續采集濾波
IIR系統的輸出不僅依賴于當前和過去的激勵輸入,而且還依賴于系統過去的輸出(反饋)。IIR系統的特性是有無限長的沖擊響應,理論上即使停止了前饋輸入,它還有系統過去的輸出繼續作為反饋輸入,從而維持輸出。如果一定要卷積IIR系統,通常要做適當的截斷和近似處理,才可以讓IIR濾波的效果在有限的計算資源使用卷積。不過雖然理論可卷,實際多用時域遞推的方式。
IIR系統的遞推計算,之前我們提供的示例C++濾波器代碼中,是為了演示,一次性批發處理多個數據,實際處理是可以根據應用來調整每次輸入數據的長度。無論是分段處理還是單個輸出,如果保留了過去的輸入和輸出狀態,是可以持續進行處理的。下面是每次輸入一個信號x(n),然后生成/讀取一個輸出y(n),一定要正確保留每次的輸出和輸入。
下面是一個簡單IIR單輸入濾波的示例,參數沒有哈。當然,把這個轉換為FIR的濾波處理也是很自然的事情。
#define N 3 // 設置濾波器的階數
double a[N] = {...}; // 這是濾波器的反饋系數
double b[N] = {...}; // 這是濾波器的前饋系數
double x[N] = {0}; // 這是輸入的緩沖數組
double y[N] = {0}; // 這是輸出的緩沖數組
double iir_filter(double input)
{
int i;
//更新輸入緩沖數組,循環更替
for (i = N - 1; i > 0; --i)
{
x[i] = x[i - 1];
}
x[0] = input;
//計算當前的輸出
double output = 0;
for (i = 0; i < N; ++i)
{
output += b[i] * x[i] - a[i] * y[i];
}
????//?更新輸出緩沖數組
for (i = N - 1; i > 0; --i)
{
y[i] = y[i - 1];
}
y[0] = output;
returnoutput;
}
如果IIR系統長數據分段沒有保存過去的狀態,我們可以得到下圖。
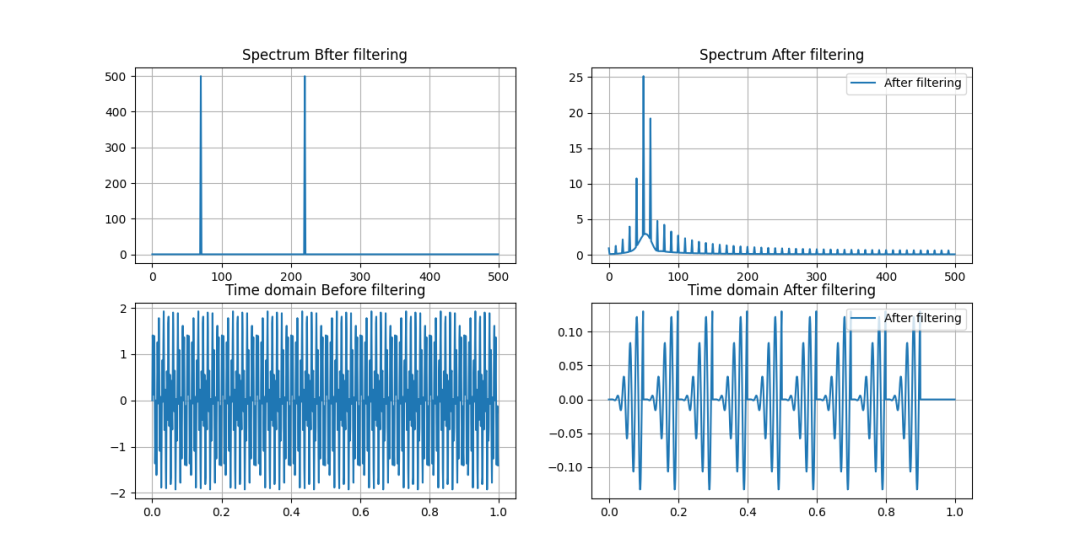
IIR分段濾波沒有保留過去的狀態
過濾沒有處理好,還生成了額外的干擾信號。總之,IIR系統中忘記歷史,就會有懲戒啊。
如果IIR系統長數據分段保存過去的狀態,我們可以得到下圖:
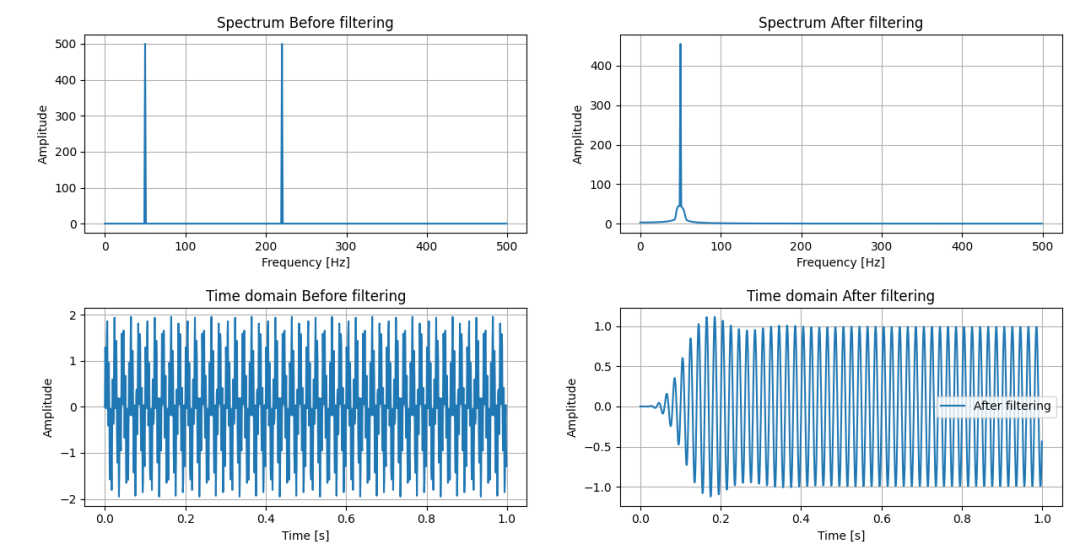
IIR分段濾波有過去的狀態
前面兩組圖相比,差異是不是一目了然?下面是IIR系統每次分段考慮了過去狀態的Python模擬代碼。
# IIR 系統分段處理:過去狀態的處理 import numpy as np import matplotlib.pyplot as plt from scipy import signal from numpy.fft import fft, fftfreq # 創建模擬信號 # 采樣頻率 Fs = 1000 nyq = 0.5 * Fs # 設定阻帶頻率 low = 45.0 high = 55.0 # 按照通帶和阻帶頻率的順序來設計濾波器 lowcut = low / nyq highcut = high / nyq # 使用iirdesign設計濾波器 b, a = signal.iirdesign([lowcut, highcut], [lowcut - 0.05, highcut + 0.05], gpass=1, gstop=60, ftype='butter', output='ba') T = 1.0 / Fs # 采樣時間間隔 t = np.arange(0, 1, T) # 創建時間軸 x = np.sin(2 * np.pi * 50 * t) + 1 * np.sin(2 * np.pi * 220 * t) # 50Hz和120Hz信號疊加 # 創建一個與x長度相同的用于保存濾波后結果的數組 y = np.zeros_like(x) # 分段進行濾波 win_size = 100 # 窗口大小 zi = signal.lfilter_zi(b, a) * x[0] # 計算初始狀態 for i in range(win_size, len(x)+1, win_size): y[i-win_size:i], zi = signal.lfilter(b, a, x[i-win_size:i], zi=zi) # 計算輸入信號和輸出信號的頻譜 frequencies = fftfreq(len(t), 1/Fs) x_spectrum = np.abs(fft(x)) y_spectrum = np.abs(fft(y)) # 繪制幅頻響應圖 w, h = signal.freqz(b, a) plt.figure() plt.plot(w/(2*np.pi), abs(h)) plt.title('Frequency response') plt.xlabel('Frequency [Hz]') plt.ylabel('Gain') plt.grid() # 繪制頻譜圖 plt.figure(figsize=(9, 6)) plt.subplot(221) plt.title('Spectrum Before filtering') plt.xlabel('Frequency [Hz]') plt.ylabel('Amplitude') plt.grid() plt.plot(frequencies[:Fs//2], x_spectrum[:Fs//2], label='Before filtering') plt.subplot(222) plt.plot(frequencies[:Fs//2], y_spectrum[:Fs//2], label='After filtering') plt.title('Spectrum After filtering') plt.xlabel('Frequency [Hz]') plt.ylabel('Amplitude') plt.grid() # 繪制模擬信號和濾波后的信號 plt.subplot(223) plt.plot(t, x, label='Before filtering') plt.title('Time domain Before filtering') plt.xlabel('Time [s]') plt.ylabel('Amplitude') plt.grid() plt.subplot(224) plt.plot(t, y, label='After filtering') plt.title('Time domain After filtering') plt.xlabel('Time [s]') plt.ylabel('Amplitude') plt.grid() plt.tight_layout() plt.legend() plt.show()
FIR系統的連續采集濾波
和IIR系統相比,FIR系統的輸出則僅僅依靠當前和過去的輸入。但是,要實現相同的濾波效果(不考慮相位線性),FIR往往要更高的階數才可以完成。階數越高,意味著越多的資源和越長的系統延遲。
我們知道,FIR濾波器中的每個系數b(n),都對應于系統的單位沖擊響應h(n)。所以,對于FIR濾波器,那我們就可以通過但不限于卷積的方式來處理信號。這里我們圍繞卷積的方式來討論FIR濾波器處理數據分段濾波的兩種方法:
重疊保留(Overlap-Save)
重疊相加(Overlap-Add)
下面兩個等式分別是卷積和FIR濾波處理。
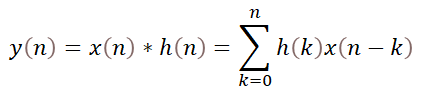
(1)
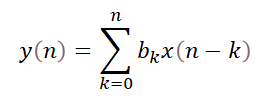
(2)
如果把b[k]看作h(k),則水到渠成,FIR濾波器的處理過程就是一個卷積運算。變成卷積后的另外的好處就是,我們可以利用FFT/IFFT來進行某些大型數據的加速運算——時域的卷積等同于頻域的乘積。對于小到中等大小的數組序列,一般也就用時域的卷積了。
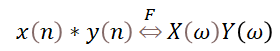
但是卷積從現象上看,當我們參與卷積的FIR濾波器長度為M,被卷積的數據序列長度為L,那么,每次卷積的結果的數據序列N長度會是:
N= M + L -1
當你面對每次多出原先數據序列長度L的結果N時?如何取舍?
如果濾波器是從全0的狀態開始的,濾波器需要一定的"預熱"時間才能達到穩定的工作狀態。濾波器的"預熱"過程就是濾波器讀取前N個樣本的過程。因此,你會看到濾波后的數據最開始部分是從0開始,然后逐漸看到正常的輸出波形。
另外,我們示例的濾波器是加窗處理的,而且模擬信號頻率比較單一,相距也較遠,否則,處理不好的濾波結果會讓人感覺出乎意外。因為每次截取一段數據,相對于給采集的數據加了一個矩形窗,而我們在設計濾波器時,是需要對這個矩形窗進行額外加窗處理的。矩形窗對于波形而言存在著頻譜泄漏和主瓣寬度等問題,對數據的處理有時候會比較麻煩。——注意,要跑題了吧?
我們看模擬結果。下圖為待濾波處理的模擬信號。500Hz+1400Hz。
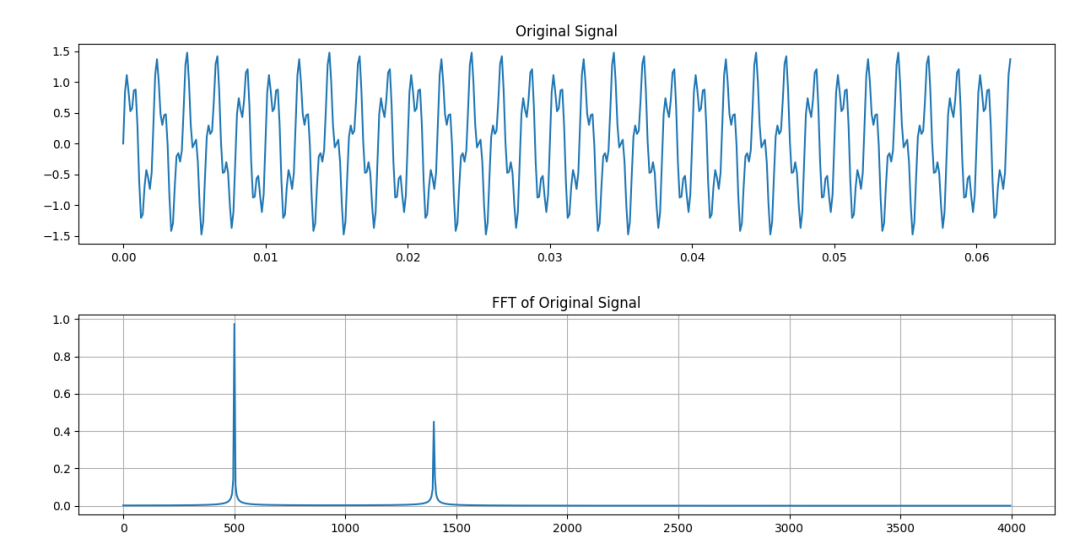
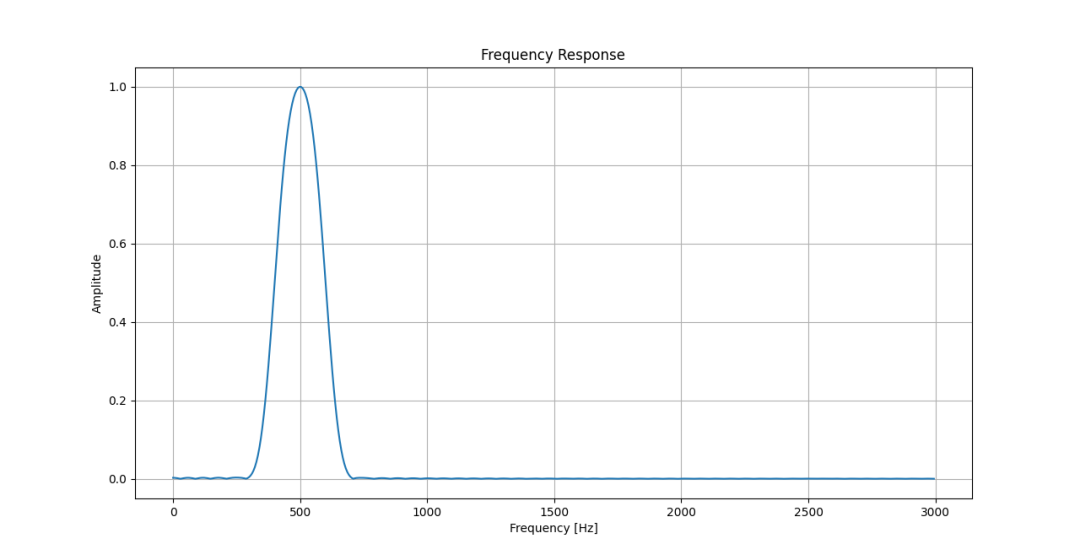
下圖為矩形窗濾波器的幅頻響應——知道為什么我要選1400Hz作為被濾掉的信號了吧?
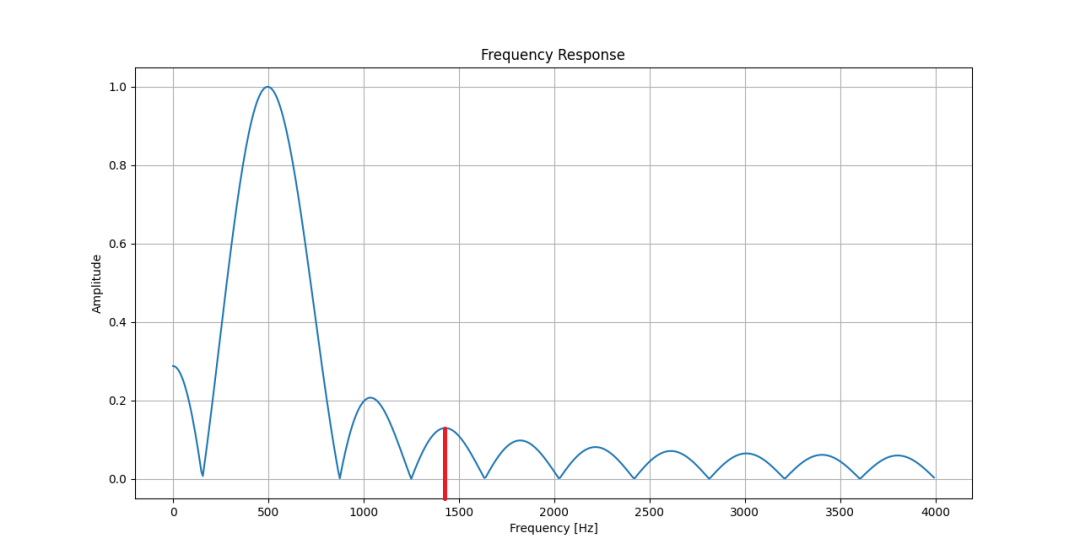
矩形窗選頻濾波器幅頻特性
這個例子僅僅是為了說明矩形窗的影響。下面是矩形窗濾波器的結果,500Hz+1400Hz的信號經過濾波之后的輸出。——跑題十萬八千里是為了一扇窗?
(忽略此圖)
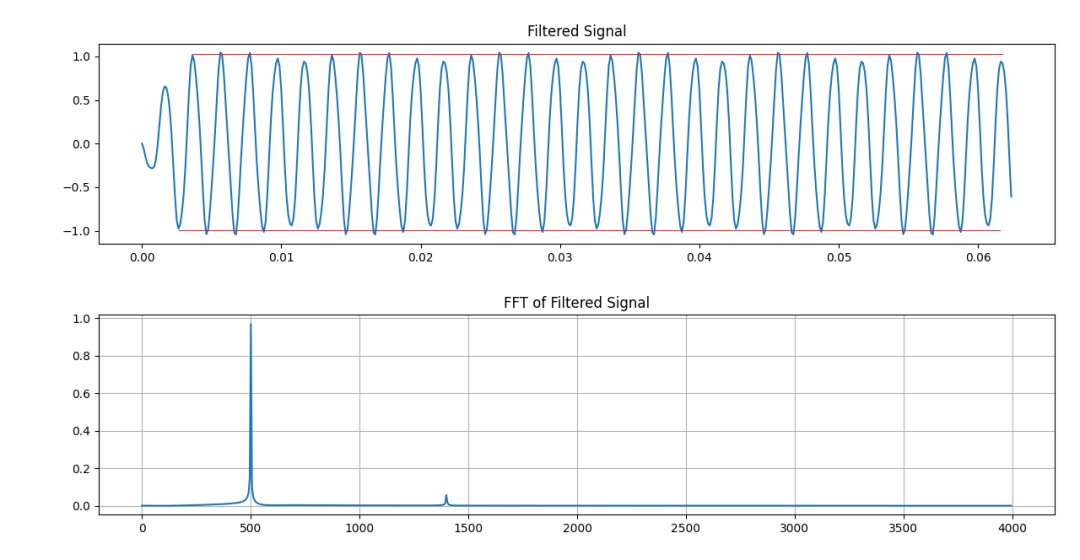
矩形窗濾波器處理結果
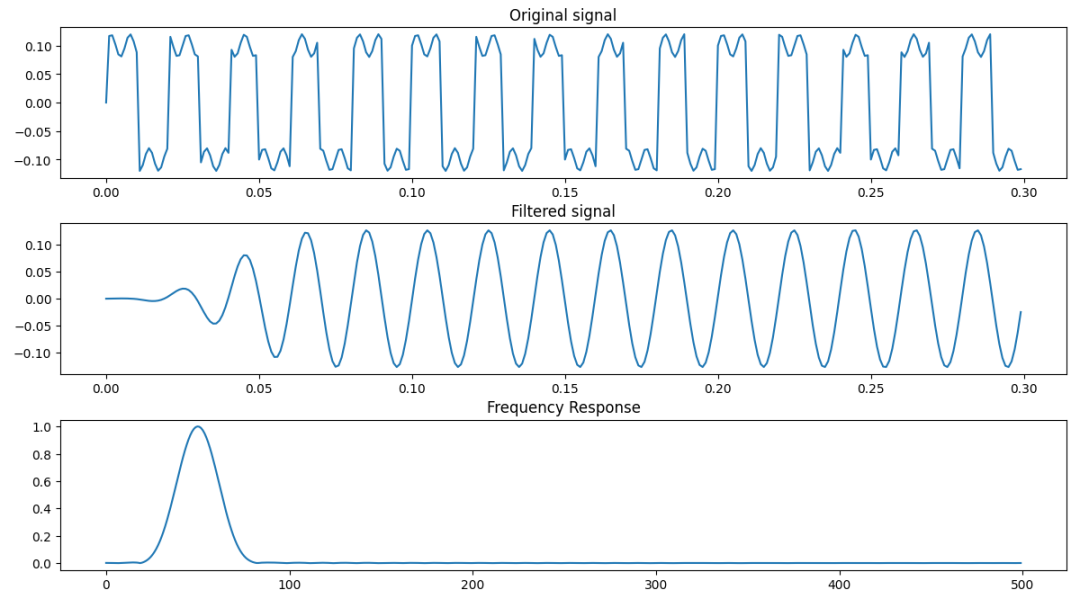
而加漢明窗的濾波結果在試驗設定條件下則要好一些,同樣留意1400Hz處。如下圖。
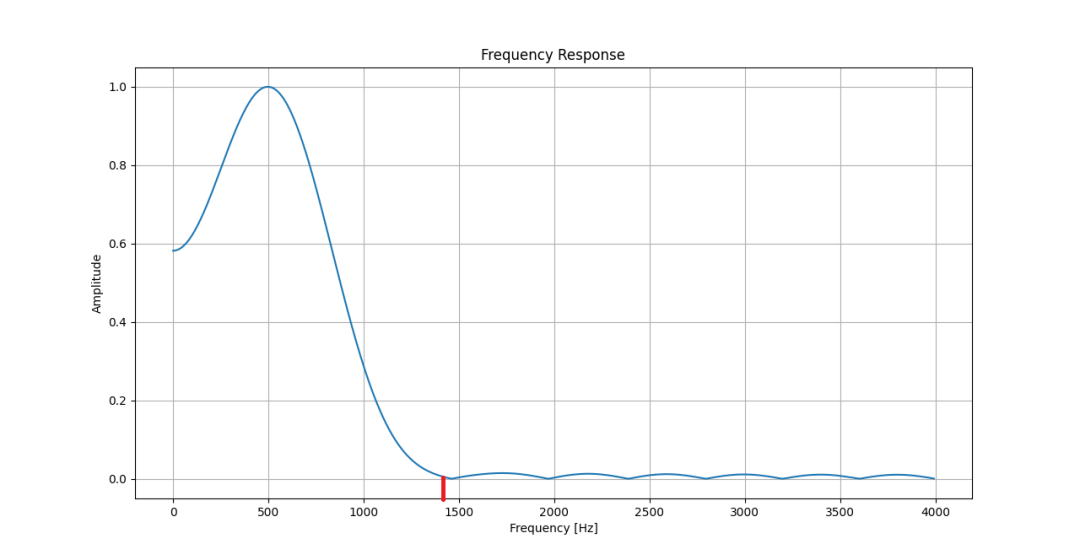
漢明窗濾波器的幅頻特性
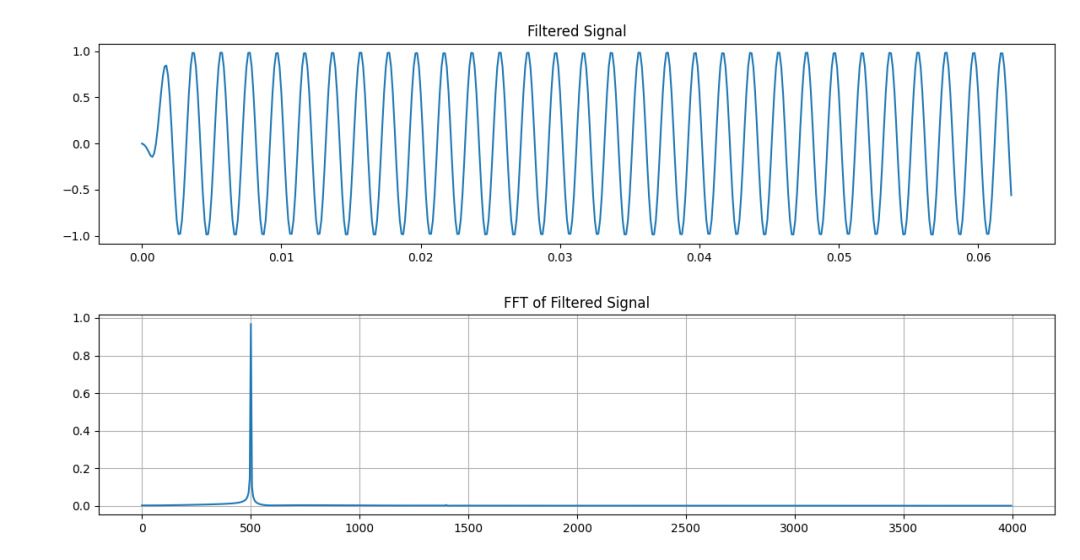
加漢明窗的濾波結果
以上處理為了差異效果,對于濾波器長度、一次處理數據長度,兩個信號頻率的距離都是作了特別的處理。誰說實際應用中不會碰到呢?
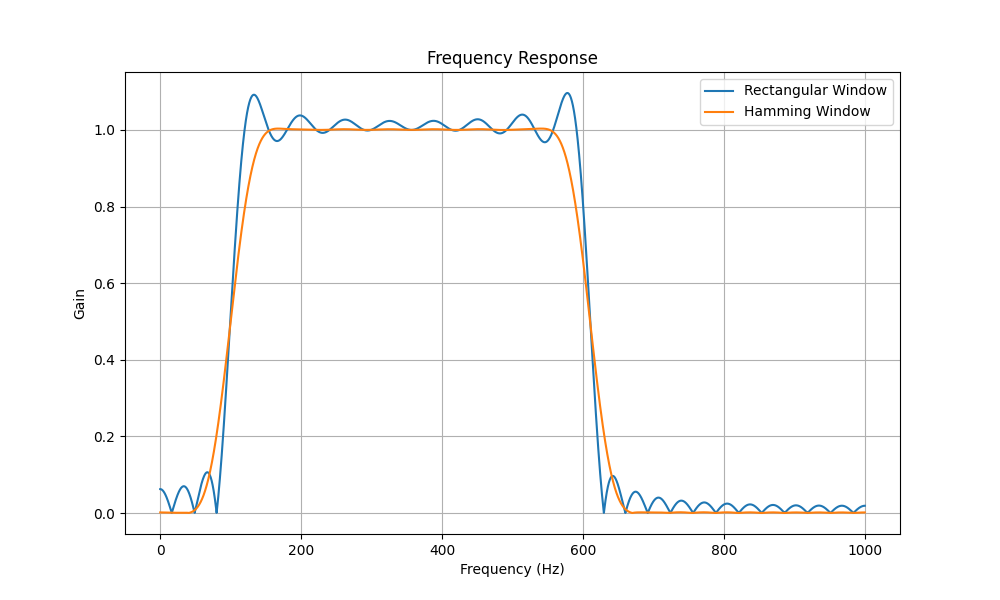
帶通濾波器不同的加窗幅頻特性
以下內容,都默認已經加窗。
我們再次回到FIR系統使用重疊保留(Overlap-Save)和重疊相加(Overlap-Add)的方式進行分段處理這個話題。
如果FIR系統在頻域通過DFT/IDFT并采用重疊保留的方式,那應該是按照下圖的方式進行的。
對于FIR濾波器長度為M,數據段長度為L時,流程大致是:在第一個數據段加M-1個0,其余的數據段都是加上前一段的最后M-1個數據;然后進行DFT/IDFT處理得到長度為(L+M-1)的y(n)序列,然后去掉前面M-1個無效值,保留后面的L個。
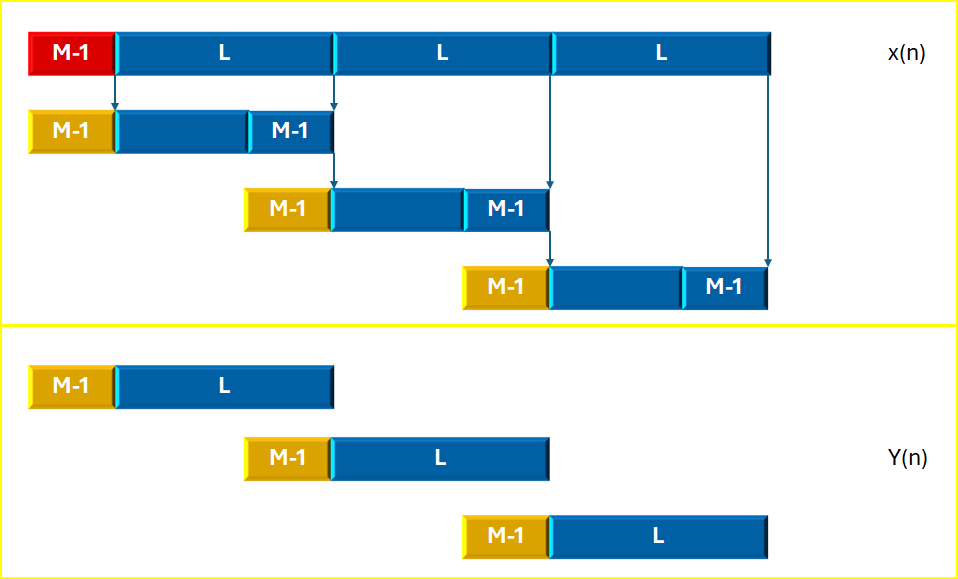
頻域中FIR系統的重疊保留法示意圖
在時域我們也想照貓畫虎的。然而,對于FIR濾波器長度為M和信號的長度L進行卷積,其結果的長度將會是M + L - 1。在實際應用中,我們通常關注的部分是兩個序列完全重疊的區域,也就是“有效值”。這意味著如果兩個參與卷積的長度不一樣(一般L>M),那最后的“有效值”是需要在卷積的結果序列上兩頭都要掐掉(M-1)個元素。所以實際卷積結果中的有效序列長度是:
[L+M-1-2(M-1)]=L-M+1
在Python中,卷積函數np.convolve(data_segment, b, mode)對指定長度的數據data_segment(長度L),和FIR濾波器系數序列b(長度M)進行卷積,而輸出的結果序列則分為以下三種:
full:結果長度=M+L-1
same:結果長度=max(M,L)
valid:結果長度=max(M,L)-min(M,L)+1=L-(M-1)
為了測試時域中的重疊保留處理方式,小編選了上面卷積函數的valid模式。
在重疊保留方式下,每次參與卷積的數據長度不是L,而是每個數據L起始處,都額外添加了(M-1)長的0(第一個)或者前一段數據的最后(M-1)個數據,再與長度為M的濾波器卷積。這種情況下,參與卷積的數據長度和生成的卷積結果長度是有變化的。
L和M長序列進行卷積得到的full長度為:M+L-1;
那如果將L+(M-1)和M長的序列進行卷積,得到的full長度為:L+(M-1)+M-1=L+2(M-1);
根據步驟2,我們把得到的full長度的結果兩邊減去(M-1)就可以得到一個長度為L的有效卷積序列值。
所以這個操作和頻域中DFT、IDFT之后得到的保留方式有差異,因為時域中卷積之后的分段結果數據的長度會由L+M-1變為L+2(M-1),最終取卷積有效值段的長度就等于[L+2(M-1)-2(M-1)]=L。
下面提供模擬仿真。輸出圖和Python模擬代碼。(沒有畫時域卷積中FIR系統的數據長度示意圖,無他,偷懶。)
在500Hz信號中混有1400Hz和2400Hz的干擾。采用分段濾波的方式對FIR濾波器進行卷積處理。我們仍然把它命名為“重疊保留法”。
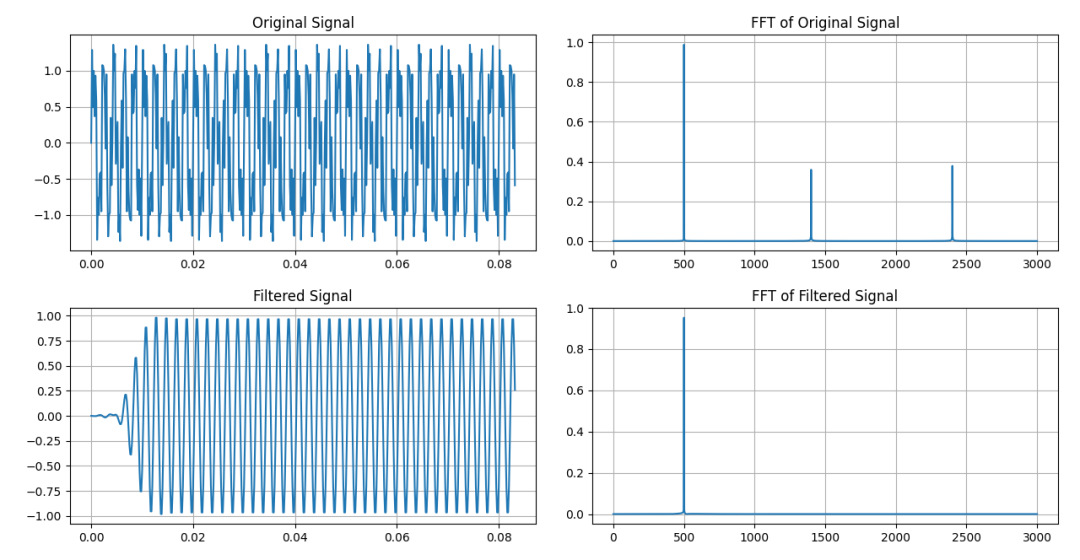
FIR系統時域卷積的重疊保留法
# FIR系統時域卷積:重疊保留法 import numpy as np import matplotlib.pyplot as plt from scipy import signal from scipy.fft import fft,fftfreq # 設置采樣率和數據長度 fs = 6000 # 創建帶通濾波器 # Create a bandpass filter f1 = 400 f2 = 600 filter_len = 100 # FIR濾波器長度 b = signal.firwin(filter_len, [f1, f2], pass_zero=False, fs=fs, window='hamming') #boxcar # 設置數據長度:模擬每次采集同樣長度的數據 # segment_len,是按照np.concatenate函數在Valid模式下卷積后有效長度來計算的 seg_filter_len = 512 # filter output length of each segment data segment_len = seg_filter_len - filter_len + 1 # 分段數據目標長度 seg_filter_len = segment_len + filter_len - 1 target_length = segment_len * 50 # 總數據長度 # 而新的時間序列的上限 TimeSpace = target_length / fs # 生成的時間序列為L的整數倍,模擬每次采樣的數據的長度 t = np.arange(0, TimeSpace, 1/fs) #產生一個含有1.4KHz,2.4KHz和500Hz信號的模擬信號,其中1.4,2.4KHz的信號將被過濾 x = np.sin(2 * np.pi * 500 * t) + 0.5 * np.sin(2 * np.pi * 1400 * t) + 0.5 * np.sin(2 * np.pi * 2400 * t) # Filter and segment with overlap-save method # each segment length should be longer than filter's length y_result = [] segment = None for i in range(0, target_length, segment_len): if i==0: # 第一段數據濾波前,前面填充(M-1)個0,再加開始的L個數據參與濾波卷積 segment = np.concatenate((np.zeros(filter_len-1), x[0:segment_len])) else: # 對后續的每個段,包括從上段的末尾取(M-1)個點,再新取L個點,這里M指濾波器長度,L指擬當前新取的數據長度 segment = np.concatenate((x[i-filter_len+1:i], x[i:i+segment_len])) # 每個段使用“valid”卷積模式,所以每次卷積后的有效數據長度是:L = L + 2(M-1) - 2(M-1) = segment_len conv = np.convolve(segment, b, mode='valid') # 與結果進行合并連接 y_result = np.concatenate((y_result, conv)) # Frequency response of filter w, h = signal.freqz(b, 1, fs=fs) plt.figure() plt.plot(w, abs(h)) plt.title('Frequency Response') # 頻率響應 plt.xlabel('Frequency [Hz]') # 頻率 plt.ylabel('Amplitude') # 幅度 plt.grid() # Plot the original signal and its FFT n = len(x) freq = fftfreq(n, 1/fs) y = fft(x) plt.figure(figsize=(9,6)) plt.subplot(221) plt.plot(t[:500], x[:500]) plt.title('Original Signal') # 原始信號 plt.grid() plt.subplot(222) plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 頻譜規范化輸出 plt.title('FFT of Original Signal') # 原始信號的FFT plt.grid() # Plot the filtered signal and its FFT n = len(y_result) freq = fftfreq(n, 1/fs) y = fft(y_result) plt.subplot(223) plt.plot(t[:500], y_result[:500]) plt.title('Filtered Signal') # 濾波后的信號 plt.grid() plt.subplot(224) plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 頻譜規范化輸出 plt.title('FFT of Filtered Signal') # 濾波后信號的FFT plt.grid() plt.tight_layout() plt.show()
大膽假設,小心求證。
以上代碼并未實證,純屬模擬,各位有興趣可以試試。
不過我們安費諾的傳感器都是久經沙場,經歷過各種工況驗證的,感興趣也可以試試。
內容長了看起來都煩,FIR時域的“重疊相加”卷積處理,下回分解。
-
數字濾波器
+關注
關注
4文章
265瀏覽量
46905 -
IIR
+關注
關注
1文章
61瀏覽量
22798 -
仿真分析
+關注
關注
2文章
102瀏覽量
33593
原文標題:數字濾波器(4)—IIR/FIR系統對連續采集數據的濾波處理和模擬仿真
文章出處:【微信號:安費諾傳感器學堂,微信公眾號:安費諾傳感器學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 IIR/FIR系統對連續采集數據的濾波處理和模擬仿真
IIR/FIR系統對連續采集數據的濾波處理和模擬仿真










評論