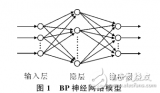
BP神經網絡(Backpropagation Neural Network)是一種多層前饋神經網絡,其拓撲結構包括輸入層、隱藏層和輸出層。下面詳細介紹BP神經網絡的拓撲結構。
- 輸入層
輸入層是BP神經網絡的第一層,用于接收外部輸入信號。輸入層的神經元數量取決于問題的特征維度。每個輸入信號通過一個權重與輸入層的神經元相連,權重的初始值通常隨機初始化。
- 隱藏層
隱藏層是BP神經網絡的核心部分,用于提取特征和進行非線性變換。隱藏層可以有多個,每個隱藏層可以包含不同數量的神經元。隱藏層的神經元數量和層數取決于問題的復雜性和需要的表達能力。
隱藏層的神經元通過權重與輸入層的神經元相連,權重的初始值通常隨機初始化。隱藏層的神經元使用激活函數進行非線性變換,常用的激活函數有Sigmoid函數、Tanh函數和ReLU函數等。
- 輸出層
輸出層是BP神經網絡的最后一層,用于生成預測結果。輸出層的神經元數量取決于問題的輸出維度。輸出層的神經元通過權重與隱藏層的神經元相連,權重的初始值通常隨機初始化。
輸出層的神經元使用激活函數進行非線性變換,常用的激活函數有Softmax函數、Sigmoid函數和線性函數等。Softmax函數常用于多分類問題,Sigmoid函數常用于二分類問題,線性函數常用于回歸問題。
- 權重和偏置
BP神經網絡中的權重和偏置是網絡的參數,用于調整神經元之間的連接強度。權重和偏置的初始值通常隨機初始化,然后在訓練過程中通過反向傳播算法進行調整。
權重是神經元之間的連接強度,用于調整輸入信號對神經元的影響。偏置是神經元的閾值,用于調整神經元的激活狀態。權重和偏置的值通過訓練數據進行優化,以最小化預測誤差。
- 激活函數
激活函數是BP神經網絡中的關鍵組成部分,用于引入非線性,使網絡能夠學習和模擬復雜的函數映射。常用的激活函數有:
- Sigmoid函數:Sigmoid函數是一種將輸入值壓縮到0和1之間的函數,其數學表達式為:f(x) = 1 / (1 + exp(-x))。Sigmoid函數在二分類問題中常用作輸出層的激活函數。
- Tanh函數:Tanh函數是一種將輸入值壓縮到-1和1之間的函數,其數學表達式為:f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))。Tanh函數在隱藏層中常用作激活函數。
- ReLU函數:ReLU函數是一種線性激活函數,其數學表達式為:f(x) = max(0, x)。ReLU函數在隱藏層中常用作激活函數,具有計算速度快和避免梯度消失的優點。
- Softmax函數:Softmax函數是一種將輸入值轉換為概率分布的函數,其數學表達式為:f(x) = exp(x) / sum(exp(x))。Softmax函數在多分類問題中常用作輸出層的激活函數。
- 損失函數
損失函數是衡量BP神經網絡預測結果與真實值之間差異的函數,用于指導網絡的訓練。常用的損失函數有:
- 均方誤差(MSE):MSE是回歸問題中最常用的損失函數,其數學表達式為:L = (1/n) * sum((y - ?)^2),其中y是真實值,?是預測值,n是樣本數量。
- 交叉熵損失(Cross-Entropy Loss):交叉熵損失是分類問題中最常用的損失函數,其數學表達式為:L = -sum(y * log(?)),其中y是真實標簽的獨熱編碼,?是預測概率。
- Hinge損失:Hinge損失是支持向量機(SVM)中常用的損失函數,用于處理線性可分問題。
- 優化算法
優化算法是BP神經網絡訓練過程中用于更新權重和偏置的算法。常用的優化算法有:
- 梯度下降(Gradient Descent):梯度下降是最常用的優化算法,通過計算損失函數關于權重和偏置的梯度,然后更新權重和偏置以最小化損失函數。
- 隨機梯度下降(Stochastic Gradient Descent, SGD):SGD是梯度下降的一種變體,每次更新只使用一個樣本或一個小批量樣本,可以加快訓練速度。
- 動量(Momentum):動量是一種優化技術,通過在梯度下降過程中加入動量項,可以加速收斂并避免陷入局部最小值。
-
拓撲結構
+關注
關注
6文章
323瀏覽量
39165 -
BP神經網絡
+關注
關注
2文章
115瀏覽量
30535 -
非線性
+關注
關注
1文章
209瀏覽量
23064 -
神經元
+關注
關注
1文章
363瀏覽量
18438
發布評論請先 登錄
相關推薦




 bp神經網絡模型拓撲結構包括哪些
bp神經網絡模型拓撲結構包括哪些










評論