神經網絡反向傳播算法(Backpropagation)是一種用于訓練人工神經網絡的算法,它通過計算損失函數關于網絡參數的梯度來更新網絡的權重和偏置。反向傳播算法是深度學習領域中最常用的優化算法之一,廣泛應用于各種神經網絡模型中,如卷積神經網絡(CNN)、循環神經網絡(RNN)和長短時記憶網絡(LSTM)等。
- 神經網絡概述
神經網絡是一種模擬人腦神經元結構的計算模型,由大量的神經元(或稱為節點)和連接這些神經元的權重組成。每個神經元接收來自其他神經元的輸入信號,通過激活函數處理后輸出信號。神經網絡通過調整這些權重來學習輸入數據的模式和特征。
1.1 神經元模型
神經元是神經網絡的基本單元,通常由輸入、權重、偏置和激活函數組成。神經元接收多個輸入信號,每個輸入信號乘以相應的權重后求和,再加上偏置,得到神經元的輸入值。然后,輸入值通過激活函數進行非線性變換,得到神經元的輸出值。
1.2 激活函數
激活函數是神經元中用于引入非線性的關鍵組件。常見的激活函數有Sigmoid函數、Tanh函數、ReLU函數等。激活函數的選擇對神經網絡的性能和收斂速度有很大影響。
1.3 損失函數
損失函數是衡量神經網絡預測結果與真實標簽之間差異的指標。常見的損失函數有均方誤差(MSE)、交叉熵損失(Cross-Entropy Loss)等。損失函數的選擇取決于具體問題和數據類型。
- 反向傳播算法原理
反向傳播算法是一種基于梯度下降的優化算法,用于最小化神經網絡的損失函數。算法的核心思想是利用鏈式法則計算損失函數關于網絡參數的梯度,然后根據梯度更新網絡的權重和偏置。
2.1 正向傳播
在正向傳播階段,輸入數據通過網絡的每層神經元進行前向傳播,直到最后一層輸出預測結果。每一層的輸出都是下一層的輸入。正向傳播的目的是計算網絡的預測結果和損失值。
2.2 損失函數計算
根據神經網絡的預測結果和真實標簽,計算損失函數的值。損失函數的選擇取決于具體問題和數據類型。常見的損失函數有均方誤差(MSE)、交叉熵損失(Cross-Entropy Loss)等。
2.3 反向傳播
在反向傳播階段,從最后一層開始,利用鏈式法則計算損失函數關于網絡參數的梯度。梯度的計算過程是自底向上的,即從輸出層到輸入層逐層進行。反向傳播的目的是找到損失函數關于網絡參數的梯度,為權重和偏置的更新提供依據。
2.4 參數更新
根據計算得到的梯度,使用梯度下降或其他優化算法更新網絡的權重和偏置。權重和偏置的更新公式為:
W = W - α * dW
b = b - α * db
其中,W和b分別表示權重和偏置,α表示學習率,dW和db分別表示權重和偏置的梯度。
- 反向傳播算法實現
3.1 初始化參數
在訓練神經網絡之前,需要初始化網絡的權重和偏置。權重和偏置的初始化方法有多種,如隨機初始化、Xavier初始化和He初始化等。權重和偏置的初始化對神經網絡的收斂速度和性能有很大影響。
3.2 前向傳播
輸入訓練數據,通過網絡的每層神經元進行前向傳播,計算每層的輸出值。在前向傳播過程中,需要保存每層的輸入值、權重、偏置和激活函數的導數,以便在反向傳播階段使用。
3.3 損失函數計算
根據網絡的預測結果和真實標簽,計算損失函數的值。損失函數的選擇取決于具體問題和數據類型。
3.4 反向傳播
從最后一層開始,利用鏈式法則計算損失函數關于網絡參數的梯度。在計算過程中,需要使用前向傳播階段保存的中間變量。
3.5 參數更新
根據計算得到的梯度,使用梯度下降或其他優化算法更新網絡的權重和偏置。
3.6 迭代訓練
重復上述過程,直到滿足停止條件,如達到最大迭代次數或損失函數值低于某個閾值。
-
神經網絡
+關注
關注
42文章
4762瀏覽量
100541 -
函數
+關注
關注
3文章
4306瀏覽量
62431 -
神經元
+關注
關注
1文章
363瀏覽量
18438 -
深度學習
+關注
關注
73文章
5492瀏覽量
120978
發布評論請先 登錄
相關推薦




 神經網絡反向傳播算法的作用是什么
神經網絡反向傳播算法的作用是什么
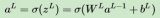










評論