非線性電路是一類具有非線性特性的電路,其輸出與輸入之間的關(guān)系不是線性的。非線性電路在電子技術(shù)、通信技術(shù)、自動(dòng)控制等領(lǐng)域有著廣泛的應(yīng)用。本文將詳細(xì)分析非線性電路的基本特點(diǎn)。
- 非線性電路的定義
非線性電路是指電路中的元件或電路本身具有非線性特性,即輸入與輸出之間的關(guān)系不是線性的。在非線性電路中,元件的電壓、電流或功率與時(shí)間的關(guān)系不是簡單的正比關(guān)系,而是滿足某種非線性函數(shù)關(guān)系。
- 非線性電路的分類
非線性電路可以根據(jù)其非線性特性的來源進(jìn)行分類,主要包括以下幾種:
2.1 電阻非線性電路
電阻非線性電路是指電路中的電阻元件具有非線性特性,如二極管、晶體管、變?nèi)荻O管等。這些元件的電壓-電流關(guān)系不是簡單的線性關(guān)系,而是滿足某種非線性函數(shù)關(guān)系。
2.2 電容非線性電路
電容非線性電路是指電路中的電容元件具有非線性特性,如變?nèi)荻O管、非線性電容等。這些元件的電荷-電壓關(guān)系不是簡單的線性關(guān)系,而是滿足某種非線性函數(shù)關(guān)系。
2.3 電感非線性電路
電感非線性電路是指電路中的電感元件具有非線性特性,如磁芯電感、非線性電感等。這些元件的磁通-電流關(guān)系不是簡單的線性關(guān)系,而是滿足某種非線性函數(shù)關(guān)系。
2.4 傳輸線非線性電路
傳輸線非線性電路是指電路中的傳輸線具有非線性特性,如非線性傳輸線、非線性耦合器等。這些元件的傳輸特性不是簡單的線性關(guān)系,而是滿足某種非線性函數(shù)關(guān)系。
- 非線性電路的數(shù)學(xué)模型
非線性電路的數(shù)學(xué)模型主要包括以下幾種:
3.1 微分方程模型
微分方程模型是描述非線性電路中電壓、電流等物理量隨時(shí)間變化的數(shù)學(xué)模型。根據(jù)電路的拓?fù)浣Y(jié)構(gòu)和元件特性,可以建立相應(yīng)的微分方程,如一階微分方程、二階微分方程等。
3.2 代數(shù)方程模型
代數(shù)方程模型是描述非線性電路中電壓、電流等物理量之間關(guān)系的數(shù)學(xué)模型。根據(jù)電路的拓?fù)浣Y(jié)構(gòu)和元件特性,可以建立相應(yīng)的代數(shù)方程,如非線性代數(shù)方程、非線性方程組等。
3.3 狀態(tài)空間模型
狀態(tài)空間模型是描述非線性電路中狀態(tài)變量隨時(shí)間變化的數(shù)學(xué)模型。狀態(tài)變量可以是電壓、電流等物理量,也可以是電路的內(nèi)部變量。狀態(tài)空間模型可以用于分析電路的穩(wěn)定性、頻率響應(yīng)等特性。
- 非線性電路的分析方法
非線性電路的分析方法主要包括以下幾種:
4.1 線性化方法
線性化方法是將非線性電路近似為線性電路進(jìn)行分析的方法。通過在工作點(diǎn)附近進(jìn)行線性化,可以得到線性電路的參數(shù),如電阻、電容、電感等。線性化方法適用于非線性程度較小的電路。
4.2 迭代法
迭代法是通過迭代求解非線性電路的數(shù)學(xué)模型的方法。首先假設(shè)一個(gè)初始解,然后根據(jù)數(shù)學(xué)模型進(jìn)行迭代計(jì)算,逐步逼近實(shí)際解。迭代法適用于非線性程度較大的電路。
4.3 符號(hào)計(jì)算法
符號(hào)計(jì)算法是利用計(jì)算機(jī)符號(hào)計(jì)算軟件對(duì)非線性電路的數(shù)學(xué)模型進(jìn)行求解的方法。符號(hào)計(jì)算法可以自動(dòng)推導(dǎo)電路的解析解或數(shù)值解,適用于復(fù)雜的非線性電路。
4.4 蒙特卡洛法
蒙特卡洛法是通過隨機(jī)抽樣對(duì)非線性電路進(jìn)行統(tǒng)計(jì)分析的方法。通過大量的隨機(jī)抽樣,可以得到電路的統(tǒng)計(jì)特性,如均值、方差等。蒙特卡洛法適用于具有隨機(jī)性的非線性電路。
- 非線性電路的穩(wěn)定性
非線性電路的穩(wěn)定性是指電路在受到擾動(dòng)后能否恢復(fù)到穩(wěn)定工作狀態(tài)的能力。非線性電路的穩(wěn)定性分析主要包括以下幾種方法:
5.1 李雅普諾夫方法
李雅普諾夫方法是利用李雅普諾夫函數(shù)對(duì)非線性電路的穩(wěn)定性進(jìn)行分析的方法。通過構(gòu)造合適的李雅普諾夫函數(shù),可以判斷電路的穩(wěn)定性。
5.2 奈奎斯特判據(jù)
奈奎斯特判據(jù)是利用奈奎斯特圖對(duì)非線性電路的穩(wěn)定性進(jìn)行分析的方法。通過繪制奈奎斯特圖,可以判斷電路的穩(wěn)定性。
5.3 伯德圖法
伯德圖法是利用伯德圖對(duì)非線性電路的頻率響應(yīng)進(jìn)行分析的方法。通過繪制伯德圖,可以判斷電路的穩(wěn)定性。
-
二極管
+關(guān)注
關(guān)注
147文章
9581瀏覽量
165956 -
元件
+關(guān)注
關(guān)注
4文章
894瀏覽量
36663 -
電子技術(shù)
+關(guān)注
關(guān)注
18文章
884瀏覽量
55873 -
非線性電路
+關(guān)注
關(guān)注
0文章
15瀏覽量
6144
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
非線性電路基礎(chǔ)課件
非線性電路混沌實(shí)驗(yàn)誤差分析電感量與哪些因素有關(guān)?
非線性電路與混沌實(shí)驗(yàn)為什么要用RC移相器呢?
非線性電路簡介
SSPA圖像傳感器的非線性電路模型
非線性電路綜合的PSPICE仿真
標(biāo)準(zhǔn)集成電路數(shù)據(jù)手冊(cè)--非線性電路
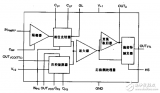
非線性電路的分析方法_非線性電路分析舉例
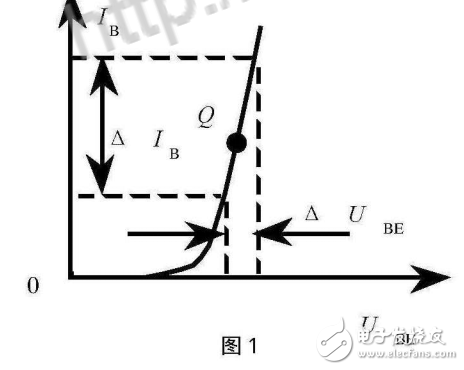




 非線性電路的基本特點(diǎn)是什么
非線性電路的基本特點(diǎn)是什么










評(píng)論