BP神經網絡(Backpropagation Neural Network)是一種多層前饋神經網絡,通過反向傳播算法進行訓練。它在許多領域,如模式識別、數據挖掘、預測分析等,都有廣泛的應用。本文將介紹如何使用Python實現BP神經網絡進行數據預測。
1. 神經網絡基礎
1.1 神經元模型
神經元是神經網絡的基本單元,它接收輸入信號,通過激活函數轉換,輸出信號。一個神經元的數學模型如下:
[ y = f(sum_{i=1}^{n} w_i x_i + b) ]
其中,( x_i ) 是輸入信號,( w_i ) 是權重,( b ) 是偏置,( f ) 是激活函數。
1.2 激活函數
激活函數用于引入非線性,使得神經網絡能夠學習和模擬復雜的函數映射。常見的激活函數包括:
- Sigmoid函數:( f(x) = frac{1}{1 + e^{-x}} )
- Tanh函數:( f(x) = tanh(x) )
- ReLU函數:( f(x) = max(0, x) )
1.3 損失函數
損失函數用于衡量模型預測值與實際值之間的差異。常見的損失函數包括:
- 均方誤差(MSE):( L = frac{1}{n} sum_{i=1}^{n} (y_i - hat{y}_i)^2 )
- 交叉熵損失:常用于分類問題。
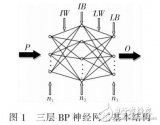
2. BP神經網絡結構
BP神經網絡由輸入層、隱藏層和輸出層組成。數據從輸入層進入,通過隱藏層的非線性變換,最終在輸出層得到預測結果。
2.1 輸入層
輸入層的神經元數量與問題的特征維度相同。
2.2 隱藏層
隱藏層可以有多個,每個隱藏層可以包含不同數量的神經元。隱藏層的數量和神經元數量需要根據具體問題進行調整。
2.3 輸出層
輸出層的神經元數量取決于問題的輸出維度。對于回歸問題,輸出層通常只有一個神經元;對于分類問題,輸出層的神經元數量等于類別數。
3. 反向傳播算法
反向傳播算法是BP神經網絡的核心,用于通過梯度下降法最小化損失函數。
3.1 前向傳播
數據從輸入層逐層傳遞到輸出層,每層的輸出作為下一層的輸入。
3.2 計算損失
使用損失函數計算模型預測值與實際值之間的差異。
3.3 反向傳播
從輸出層開始,逐層計算梯度,更新權重和偏置。
4. Python實現BP神經網絡
4.1 導入庫
import numpy as np
4.2 初始化網絡參數
def initialize_parameters(layers):
params = {}
for i in range(1, len(layers)):
params['W' + str(i)] = np.random.randn(layers[i], layers[i-1]) * 0.01
params['b' + str(i)] = np.zeros((layers[i], 1))
return params
4.3 激活函數及其導數
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x * (1 - x)
4.4 前向傳播
def forward_propagation(X, parameters):
caches = {}
A = X
for i in range(1, len(parameters) // 2 + 1):
W = parameters['W' + str(i)]
b = parameters['b' + str(i)]
Z = np.dot(W, A) + b
A = sigmoid(Z)
caches['A' + str(i)] = A
caches['Z' + str(i)] = Z
return A, caches
4.5 計算損失
def compute_cost(A3, Y):
m = Y.shape[1]
cost = (1 / m) * np.sum((A3 - Y) ** 2)
return cost
4.6 反向傳播
def backward_propagation(parameters, caches, X, Y):
grads = {}
m = X.shape[1]
A3 = caches['A3']
dA3 = - (np.divide(Y, A3) - np.divide(
-
數據
+關注
關注
8文章
6888瀏覽量
88825 -
BP神經網絡
+關注
關注
2文章
115瀏覽量
30533 -
python
+關注
關注
56文章
4782瀏覽量
84449 -
輸入信號
+關注
關注
0文章
446瀏覽量
12536
發布評論請先 登錄
相關推薦
用matlab編程進行BP神經網絡預測時如何確定最合適的,BP模型
labview BP神經網絡的實現
如何設計BP神經網絡圖像壓縮算法?
基于BP神經網絡的PID控制
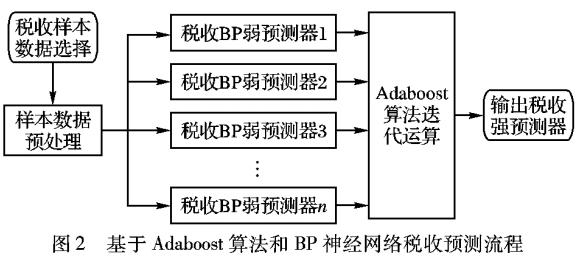
BP神經網絡的稅收預測




 python做bp神經網絡預測數據
python做bp神經網絡預測數據











評論