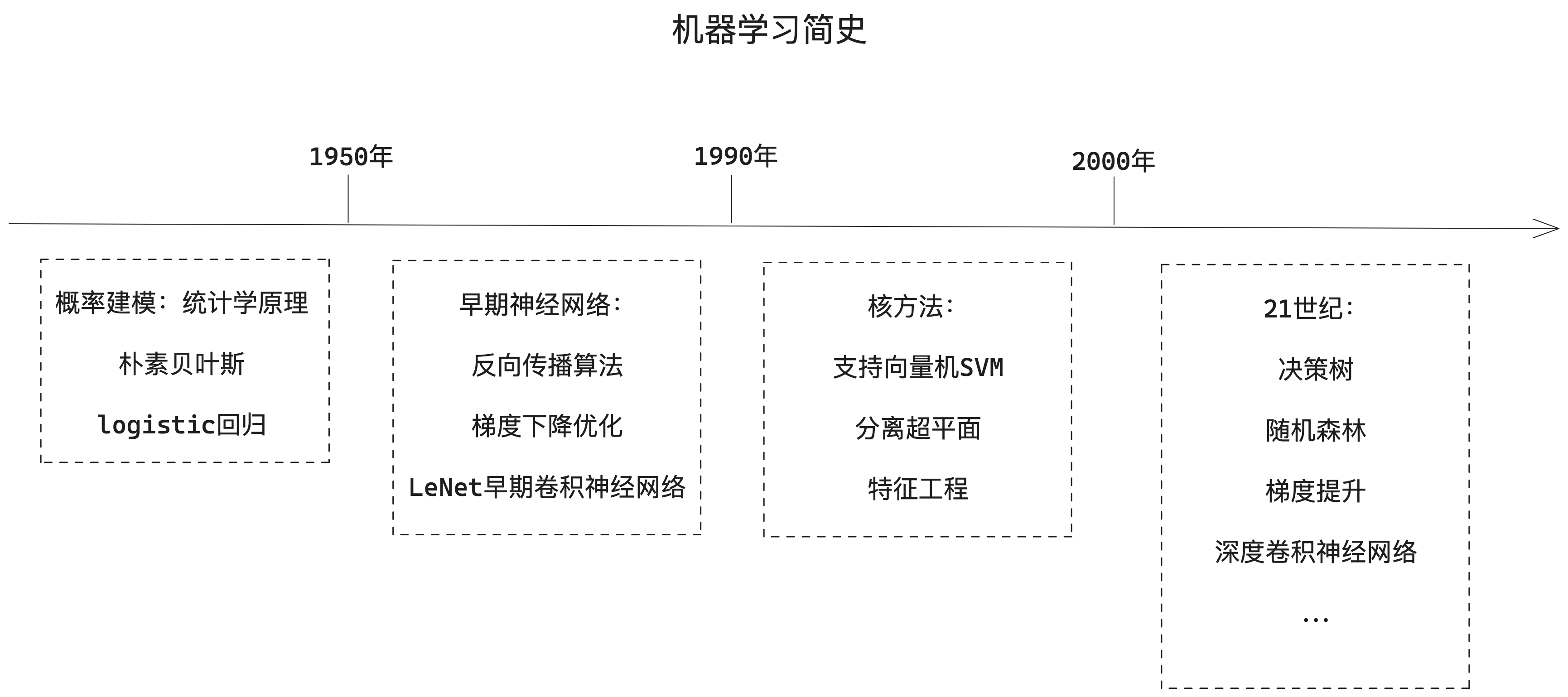
1、什么是深度學(xué)習(xí)

1.1、機器學(xué)習(xí)

??

圖1：計算機有效工作的常用方法：程序員編寫規(guī)則（程序），計算機遵循這些規(guī)則將輸入數(shù)據(jù)轉(zhuǎn)換為適當(dāng)?shù)拇鸢浮＿@一方法被稱為符號主義人工智能，適合用來解決定義明確的邏輯問題，比如早期的PC小游戲：五子棋等，但是像圖像分類、語音識別或自然語言翻譯等更復(fù)雜、更模糊的任務(wù)，難以給出明確的規(guī)則。

圖2：機器學(xué)習(xí)把這個過程反了過來：機器讀取輸入數(shù)據(jù)和相應(yīng)的答案，然后找出應(yīng)有的規(guī)則。機器學(xué)習(xí)系統(tǒng)是訓(xùn)練出來的，而不是明確的用程序編寫出來。舉個例子，如果你想為度假照片添加標(biāo)簽，并希望將這項任務(wù)自動化，那么你可以將許多人工打好標(biāo)簽的照片輸人機器學(xué)習(xí)系統(tǒng)，系統(tǒng)將學(xué)會把特定照片與特定標(biāo)簽聯(lián)系在一起的統(tǒng)計規(guī)則。

定義：機器學(xué)習(xí)就是在預(yù)定義的可能性空間中，利用反饋信號的指引，在輸入數(shù)據(jù)中尋找有用的表示和規(guī)則。

??

1.2、深度學(xué)習(xí)

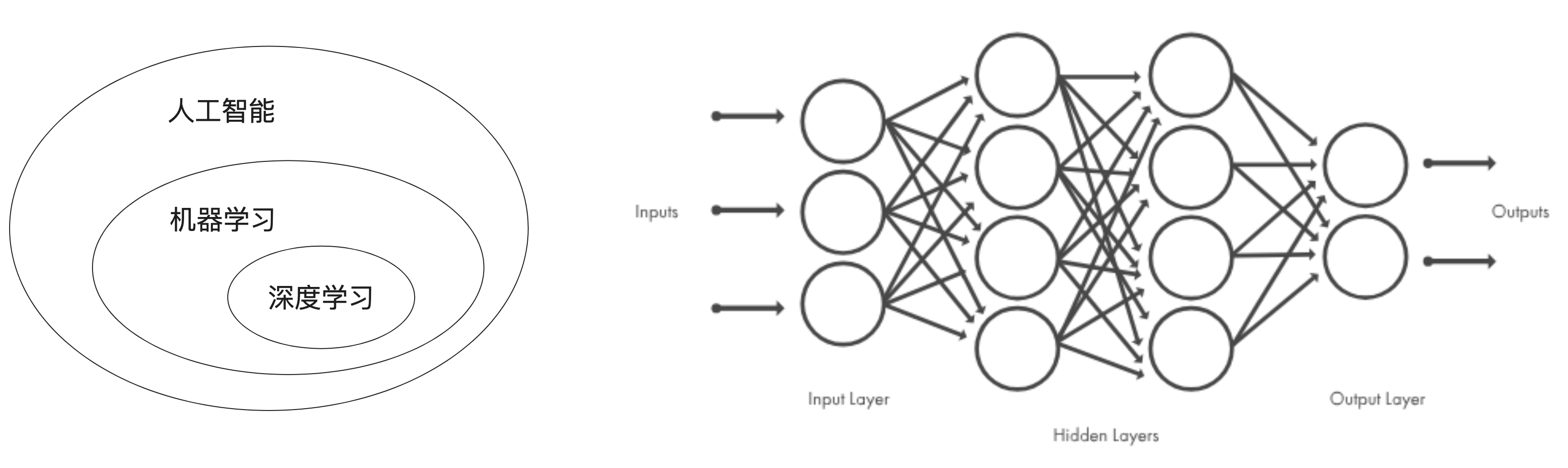
深度學(xué)習(xí)是機器學(xué)習(xí)的一個分支領(lǐng)域，強調(diào)從一系列連續(xù)的表示層中學(xué)習(xí)。現(xiàn)代的深度學(xué)習(xí)模型通常包含數(shù)十個甚至上百個連續(xù)的表示層，它們都是從訓(xùn)練數(shù)據(jù)中自動學(xué)習(xí)而來。與之對應(yīng)，機器學(xué)習(xí)有時也被稱為淺層學(xué)習(xí)。

在深度學(xué)習(xí)中，這些分層表示是通過叫作神經(jīng)網(wǎng)絡(luò)的模型學(xué)習(xí)得到的。深度神經(jīng)網(wǎng)絡(luò)可以看作多級信息蒸餾過程：信息穿過連續(xù)的過濾器，其純度越來越高。

技術(shù)定義：一種多層的學(xué)習(xí)數(shù)據(jù)表示的方法。

??

1.3、深度學(xué)習(xí)工作原理

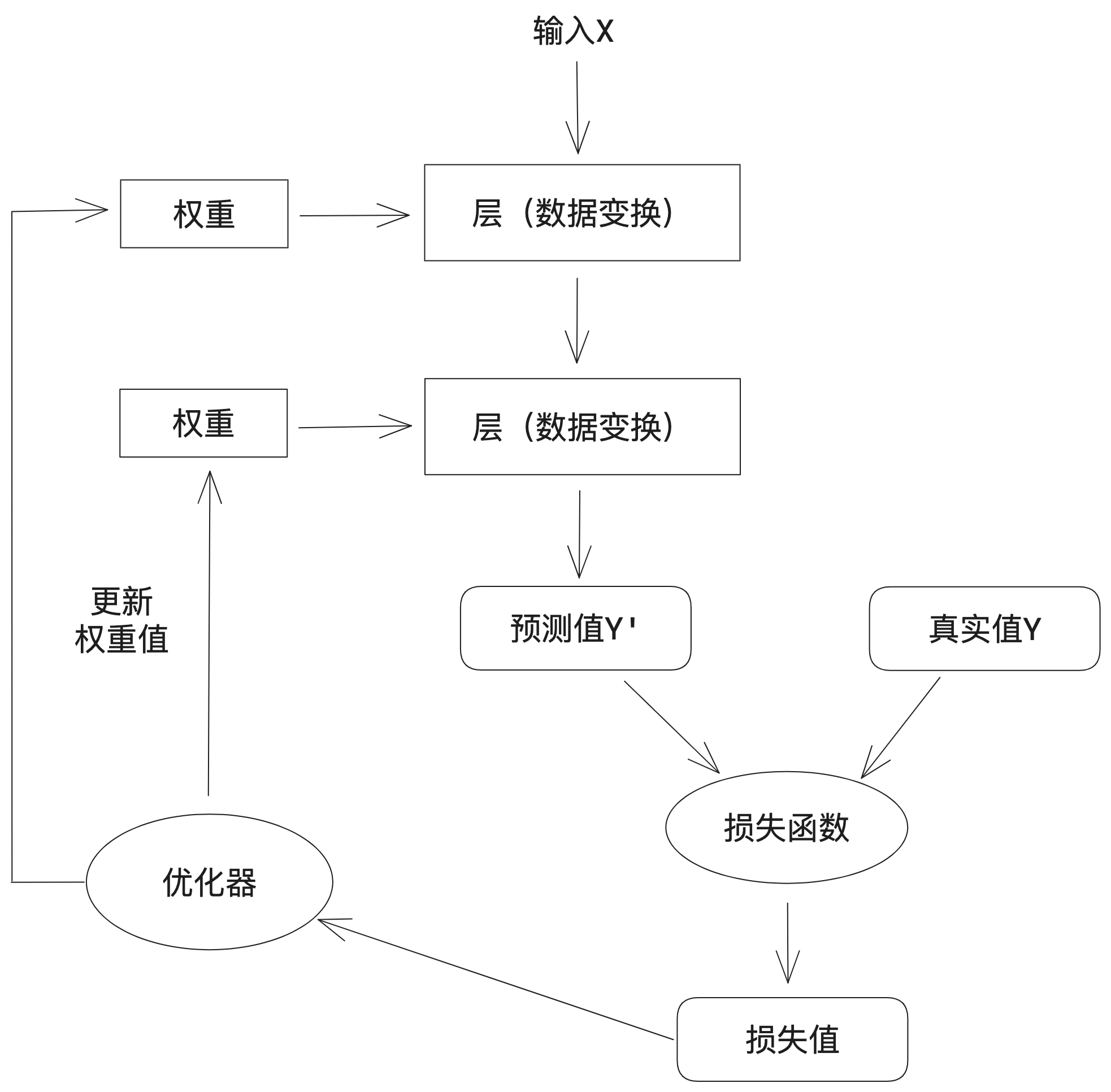
a. 對神經(jīng)網(wǎng)絡(luò)的權(quán)重（有時也被稱為該層的參數(shù)）進行隨機賦值

b. 經(jīng)過一系列隨機變換，得到預(yù)測值Y'

c. 通過損失函數(shù)（有時也被稱為目標(biāo)函數(shù)或代價函數(shù)），得到預(yù)測值Y'與真實值Y之間的損失值

d. 將損失值作為反饋信號，通過優(yōu)化器來對權(quán)重值進行微調(diào)，以降低當(dāng)前示例對應(yīng)的損失值

e. 循環(huán)重復(fù)足夠做的次數(shù)（b-d），得到具有最小損失值的神經(jīng)網(wǎng)絡(luò)，就是一個訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)

??

2、神經(jīng)網(wǎng)絡(luò)數(shù)學(xué)基礎(chǔ)

2.1、神經(jīng)網(wǎng)絡(luò)的數(shù)據(jù)表示

目前所有機器學(xué)習(xí)系統(tǒng)都使用張量（tensor）作為基本數(shù)據(jù)結(jié)構(gòu)，張量對這個領(lǐng)域非常重要，TensorFlow就是以它來命名。

張量這一概念的核心在于，它是一個數(shù)據(jù)容器。它包含的數(shù)據(jù)通常是數(shù)值數(shù)據(jù)，因此它是一個數(shù)字容器。你可能對矩陣很熟悉，它是2階張量。張量是矩陣向任意維度的推廣，張量的維度通常叫做軸。

張量是由以下3個關(guān)鍵屬性來定義的。

?軸：軸的個數(shù)

?形狀：表示張量沿每個軸的維度大小（元素個數(shù)）

?數(shù)據(jù)類型（dtype）：數(shù)據(jù)的類型，可以是float16、float32、float64、unit8、string等

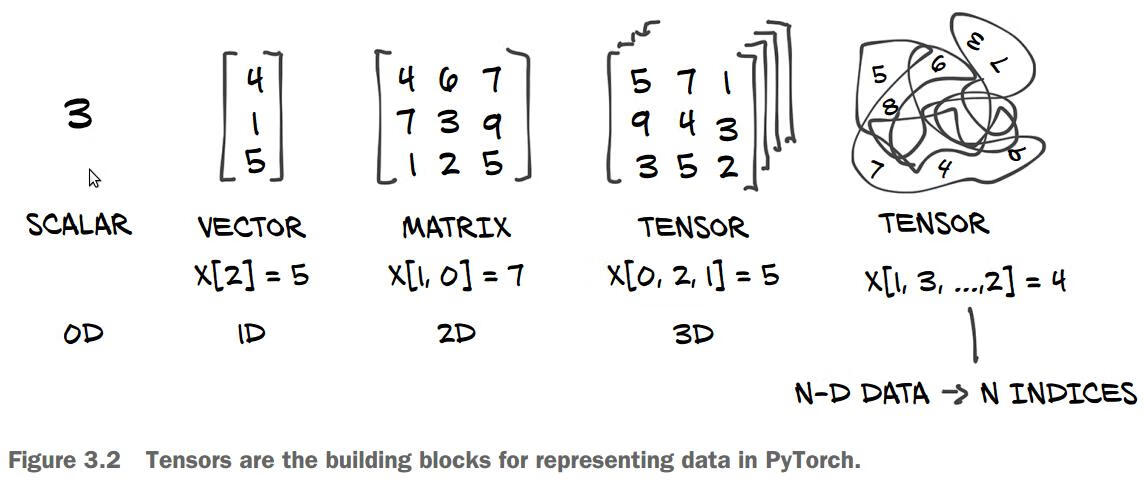
2.1.1、標(biāo)量（0階張量）

僅包含一個數(shù)字的張量叫做標(biāo)量（SCALAR），也叫0階張量或0維張量。

下面是一個NumPy標(biāo)量

import numpy as np
x = np.array(3)
x.ndim // 軸：0, 形狀：()

2.1.2、向量（1階張量）

數(shù)字組成的數(shù)組叫做向量（VECTOR），也叫1階張量或1維張量。

下面是一個NumPy向量

x = np.array([4, 1, 5])
x.ndim // 軸：1, 形狀：(3,)

這個向量包含3個元素，所以也叫3維向量。不要把3維向量和3維張量混為一談，3維向量只有一個軸，沿著這個軸有3個維度。

2.1.3、矩陣（2階張量）

向量組成的數(shù)組叫做矩陣（MATRIX），也2階張量或2維張量。矩陣有2個軸：行和列。

下面是一個NumPy矩陣

x = np.array([
    [4, 6, 7],
    [7, 3, 9],
    [1, 2, 5]
])
x.ndim // 軸：2, 形狀：(3, 3)

現(xiàn)實世界中的向量實例：

向量數(shù)據(jù)：形狀為（samples, features）的2階張量，每個樣本都是一個數(shù)值（特征）向量，向量數(shù)據(jù)庫存儲的基本單位。

2.1.4、3階張量與更高階的張量

將多個矩陣打包成一個新的數(shù)組，就可以得到一個3階張量（或3維張量）

下面是一個3階NumPy張量

x = np.array([
    [[4, 6, 7],
    [7, 3, 9],
    [1, 2, 5]],
    [[5, 7, 1],
    [9, 4, 3],
    [3, 5, 2]]
])
x.ndim // 軸：3, 形狀：(2, 3, 3)

將多個3階張量打包成一個數(shù)組，就可以創(chuàng)建一個4階張量。

現(xiàn)實世界中的實例：

時間序列數(shù)據(jù)或序列數(shù)據(jù)：形狀為（samples, timesteps, features）的3階張量，每個樣本都是特征向量組成的序列（序列長度為timesteps）

圖像數(shù)據(jù)：形狀為（samples, height, width, channels）的4階張量，每個樣本都是一個二維像素網(wǎng)格，每個像素則由一個“通道”（channel）向量表示。

視頻數(shù)據(jù)：形狀為（samples, frames, height, width, channels）的5階張量，每個樣本都是由圖像組成的序列（序列長度為frames）。

??

2.2、神經(jīng)網(wǎng)絡(luò)的“齒輪”：張量運算

所有計算機程序最終都可以簡化為對二進制輸入的一些二進制運算，與此類似，深度神經(jīng)網(wǎng)絡(luò)學(xué)到的所有變換也都可以簡化為對數(shù)值數(shù)據(jù)張量的一些張量運算或張量函數(shù)。

2.2.1、逐元素運算

逐元素運算，即該運算分別應(yīng)用于張量的每個元素。參與運算的張量的形狀必須相同。

import numpy as np
z = x + y // 逐元素加法
z = x - y // 逐元素加法
z = x * y // 逐元素乘積
z = x / y // 逐元素除法
z = np.maximum(z, 0.) //逐元素relu，大于0輸出等于輸入，小于0則輸出為0

rule運算是一種常用的激活函數(shù)，rule(x)就是max(x, 0)：如果輸入x大于0，則輸出等于輸入值；如果輸入x小于等于0，則輸出為0。

2.2.2、張量積

張量積或點積是最常見且最有用的張量運算之一。注意，不要將其與逐元素乘積弄混。

在NumPy中使用np.dot函數(shù)來實現(xiàn)張量積：z = np.dot(x, y)

數(shù)學(xué)符號中的（·）表示點積運算：z = x · y

?兩個向量的點積是一個標(biāo)量，而且只有元素個數(shù)相同的向量才能進行點積運算。

?一個矩陣x和一個向量y做點積運算，其返回值是一個向量，其中每個元素是y和x每一行的點積。

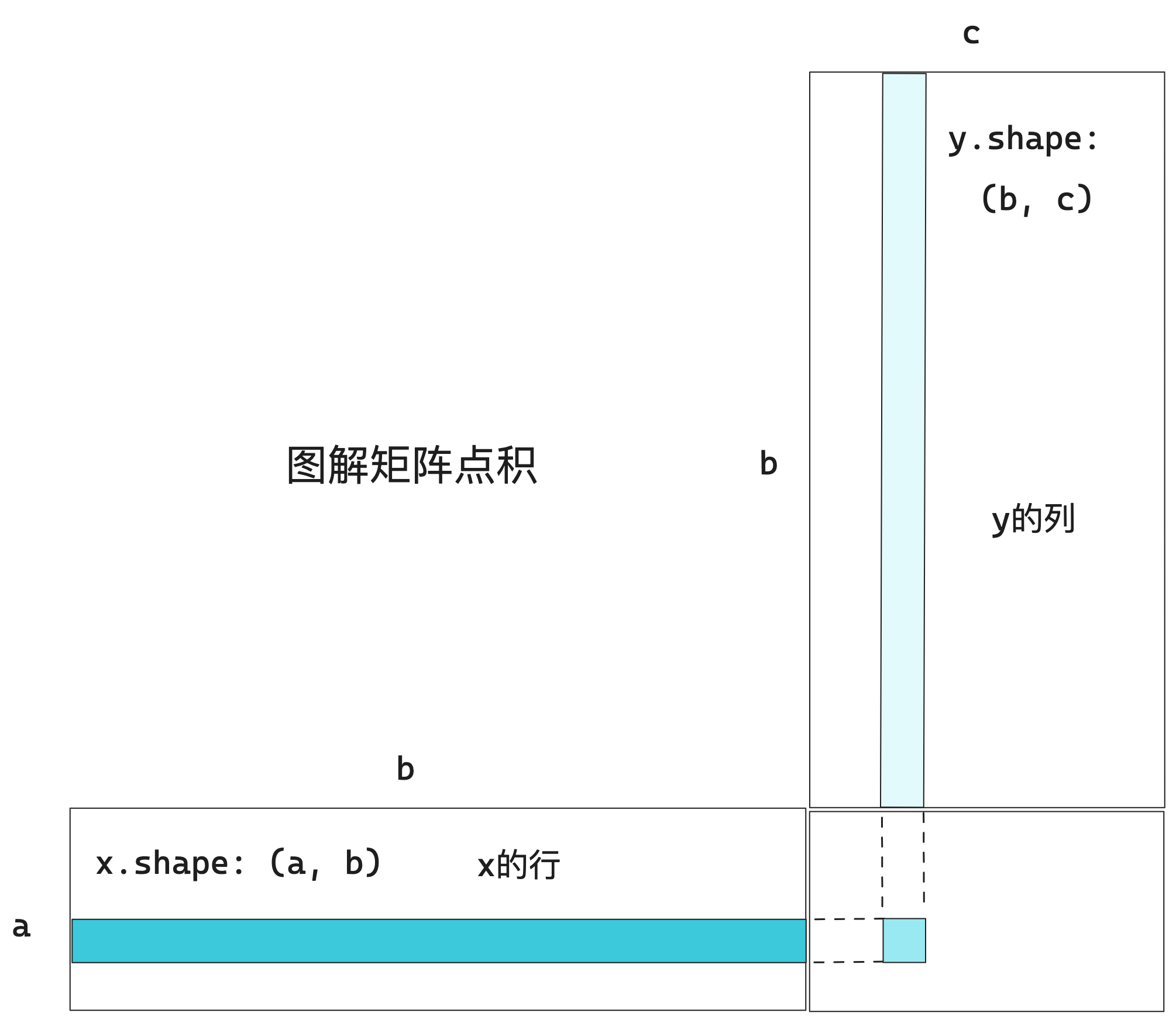
?對于矩陣x和y，當(dāng)且僅當(dāng)x.shape[1] == y.shape[0]時，才可以計算點積，其結(jié)果是一個形狀為(x.shape[0], y.shape[1])的矩陣，其元素是x的行與y的列之間的向量點積。

??

2.2.3、張量變形

張量變形是指重新排列張量的行和列，以得到想要的形狀。變形后，張量的元素個數(shù)與初始張量相同。

import numpy as np
x = np.array([[0, 1],
              [2, 3]
              [4, 5]])
x.shape //(3, 2)
x = x.reshape((6, 1))
>>> x 
array([[0],
       [1],
       [2],
       [3],
       [4],
       [5]])
x = x.reshape(2, 3)
>>> x
array([[0, 1, 2],
       [3, 4, 5]])

常見的一種特殊的張量變形是轉(zhuǎn)置。矩陣轉(zhuǎn)置是指將矩陣的行和列互換，即x[i, :]變?yōu)閤[:, i]

x = np.zeros((300, 20)) //創(chuàng)建一個形狀為(300, 20)的零矩陣
x = np.transpose(x)
>>> x.shape
(20, 300)

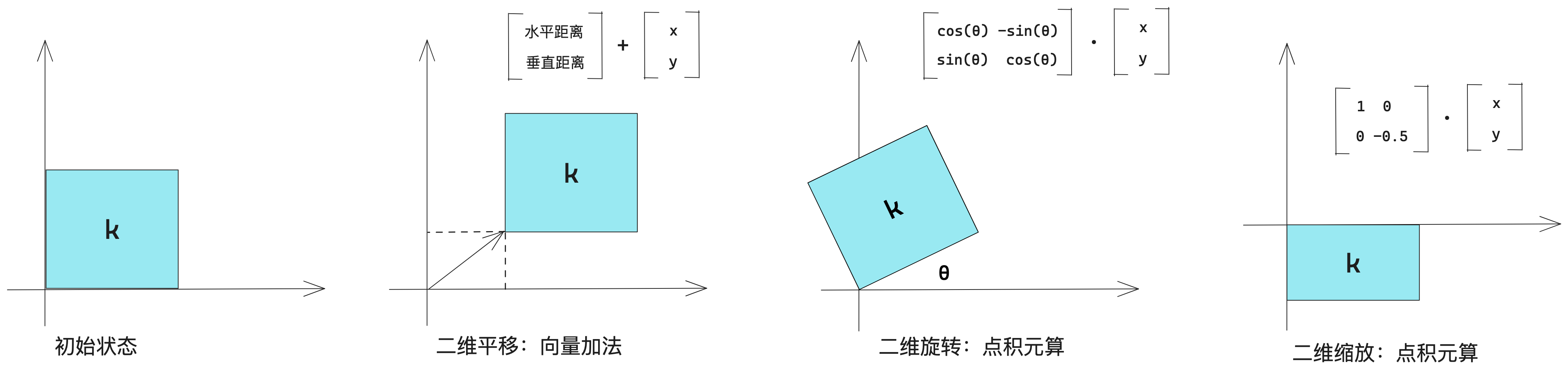
2.2.4、張量運算的幾何解釋

平移、旋轉(zhuǎn)、縮放、傾斜等基本的幾何操作都可以表示為張量運算。

??

?線性變換：與任意矩陣做點積運算，都可以實現(xiàn)一次線性變換。縮放和旋轉(zhuǎn)，都屬于線性變換。

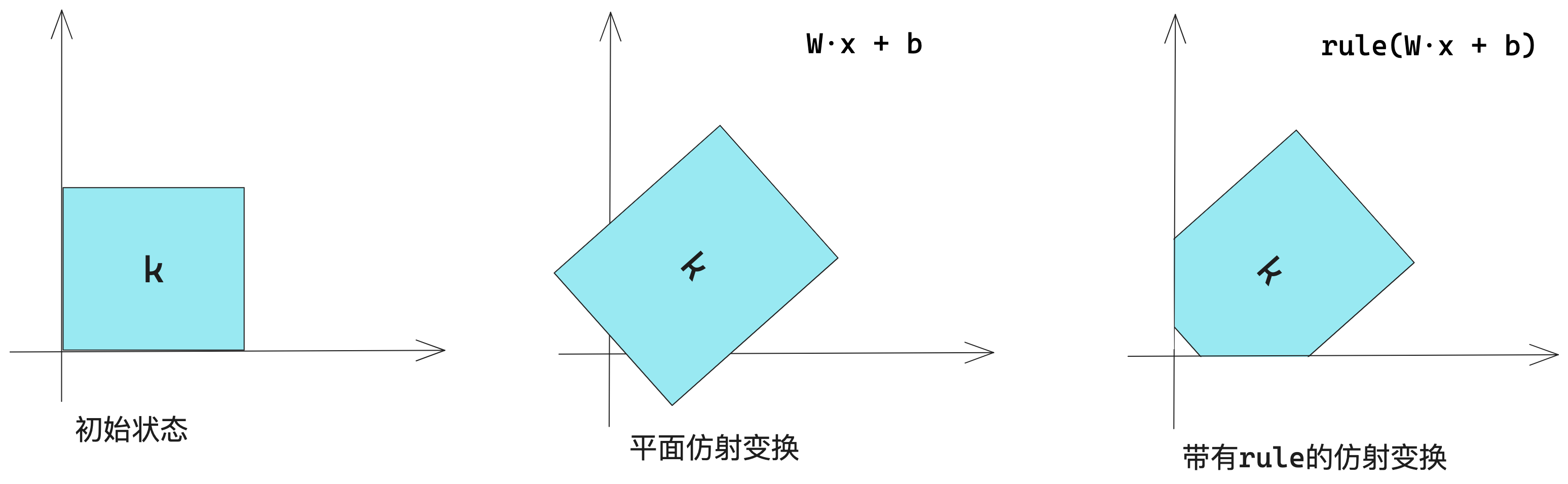
?仿射變換：一次線性變換與一次平移的組合。

?帶有rule激活函數(shù)的仿射變換：多次仿射變換相當(dāng)于一次仿射變換，因此一個完全沒有激活函數(shù)的多層神經(jīng)網(wǎng)絡(luò)等同于一層，這種“深度”神經(jīng)網(wǎng)絡(luò)其實就是一個線性模型。

??

2.2.5、深度學(xué)習(xí)的幾何解釋

神經(jīng)網(wǎng)絡(luò)完全由一系列張量運算組成，而這些張量運算只是輸入數(shù)據(jù)的簡單幾何變換。因此，你可以將神經(jīng)網(wǎng)絡(luò)解釋為高維空間中非常復(fù)雜的幾何變換，這種變換通過一系列簡單步驟來實現(xiàn)。

機器學(xué)習(xí)的目的：為高維空間中復(fù)雜、高度折疊的數(shù)據(jù)流行（一個連續(xù)的表面）找到簡潔的表示。深度學(xué)習(xí)可以將復(fù)雜的幾何變換逐步分解為一系列基本變換。

2.3、神經(jīng)網(wǎng)絡(luò)的“引擎”：基于梯度的優(yōu)化

回顧1.3章節(jié)【深度學(xué)習(xí)工作原理】，步驟a看起來很簡單，只是輸入/輸出（I/O）的代碼。步驟b、c僅僅是應(yīng)用了一些張量運算。難點在于步驟d：更新模型權(quán)重。對于模型的某個權(quán)重系數(shù)，你怎么知道這個系數(shù)應(yīng)該增大還是減小，以及變化多少？

一種簡單的解決方案是，保持模型的其他權(quán)重不變，只考慮一個標(biāo)量系數(shù)，讓其嘗試不同的取值。對于模型的所有系數(shù)都要重復(fù)這一過程。但這種方法非常低效，因為系數(shù)有很多（通常有上千個，甚至多達百萬個）。幸運的是，有一種更好的方法：梯度下降法。

2.3.1、導(dǎo)數(shù)

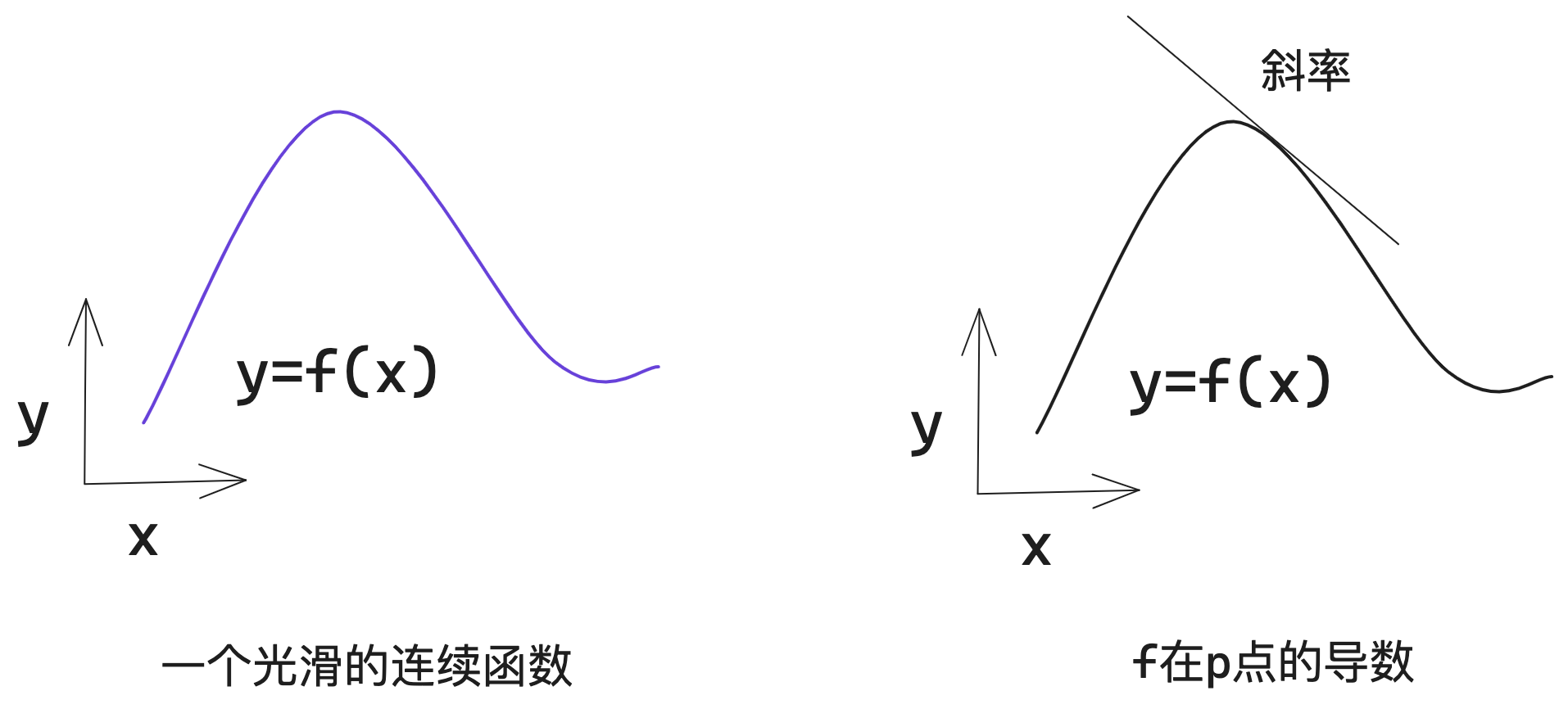
假設(shè)有一個光滑連續(xù)的函數(shù)f(x) = y，由于函數(shù)是連續(xù)的，因此x的微小變化只會導(dǎo)致y的微小變化。因此在某個點p附近，如果x變化足夠小，就可以將f近似看作斜率為a的線性函數(shù)。

斜率a被稱為f在p點的導(dǎo)數(shù)。如果a < 0，說明x在p點附近的微增將導(dǎo)致f(x)減小；如果a > 0，那么x在p點附近的微增將導(dǎo)致f(x)增大；

?

??

2.3.2、梯度

導(dǎo)數(shù)這一概念可以應(yīng)用于任何函數(shù)，只要函數(shù)所對應(yīng)的表面是連續(xù)且光滑的。張量運算的導(dǎo)數(shù)叫做梯度。對于一個標(biāo)量函數(shù)來說，導(dǎo)數(shù)是表示函數(shù)曲線的局部斜率，張量函數(shù)的梯度表示該函數(shù)所對應(yīng)多維表面的曲率。

舉例來說，物體位置相對于時間的梯度是這個物體的速度，二階梯度則是它的加速度。

2.3.3、隨機梯度下降

步驟d中更新模型權(quán)重，假設(shè)我們要處理的是一個可微函數(shù)，可以計算出它的梯度，沿著梯度的反方向更新權(quán)重，每次損失都會減小一點。

（1）抽取訓(xùn)練樣本x和對應(yīng)目標(biāo)y_true組成的一個數(shù)據(jù)批量

（2）在x上運行模型，得到預(yù)測值y_pred（前向傳播）

（3）計算模型在這批數(shù)據(jù)上的損失值

（4）計算損失相對于模型參數(shù)的梯度（反向傳播）

（5）將參數(shù)沿著梯度的反方向移動一小步，從而減小損失值

這個方法叫做小批量隨機梯度下降（SGD），隨機是指每批數(shù)據(jù)都是隨機抽取的；如果每次迭代都在所有數(shù)據(jù)上運行，這叫做批量梯度下降，但是計算成本高得多，折中辦法是選擇合理的小批量大小。

神經(jīng)網(wǎng)絡(luò)的每一個權(quán)重系數(shù)都是空間中的一個自由維度，為了對損失表面有更直觀的認識，可以將沿著二維損失表面的梯度下降可視化，但你不可能將神經(jīng)網(wǎng)絡(luò)的真實訓(xùn)練過程可視化，因為無法用人類可以理解的方式來可視化1 000 000維空間。這些低維表示中建立的直覺，實踐中不一定總是準(zhǔn)確的。

??

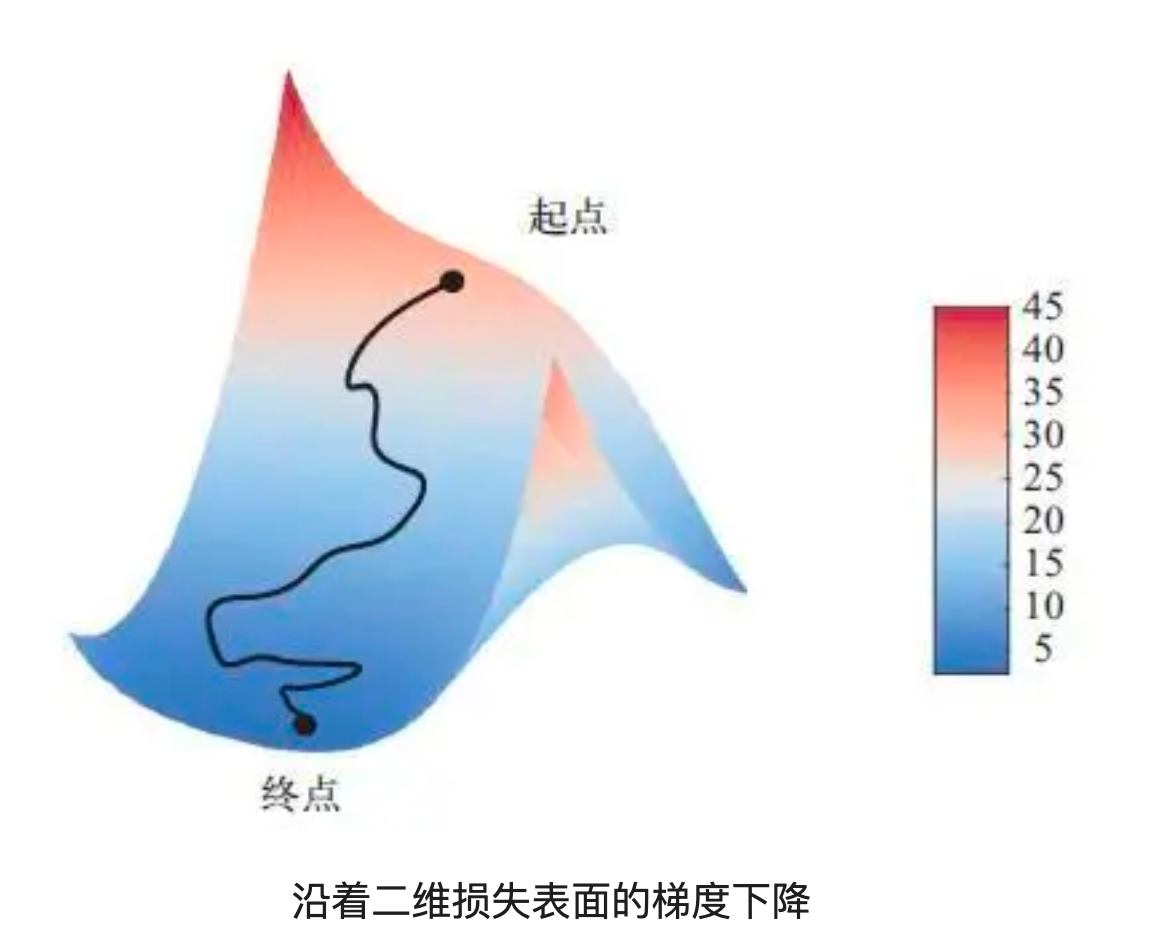
2.3.4、鏈?zhǔn)角髮?dǎo)：反向傳播

在前面的算法中，我們假設(shè)函數(shù)是可微（可以被求導(dǎo)）的，所以很容易計算其梯度。但是在實踐中如何計算復(fù)雜表達式的梯度？這時就需要用到反向傳播算法。

（1）鏈?zhǔn)椒▌t

利用簡單運算（如加法、rule或張量積）的導(dǎo)數(shù)，可以輕松計算出這些基本運算的任意復(fù)雜組合的梯度。鏈?zhǔn)椒▌t規(guī)定：grad(y, x) == grad(y, x1) * grad(x1, x)，因此只要知道f和g的導(dǎo)數(shù)，就可以求出fg的導(dǎo)數(shù)。如果添加更多的中間函數(shù)，看起來就像是一條鏈。將鏈?zhǔn)椒▌t應(yīng)用于神經(jīng)網(wǎng)絡(luò)梯度值的計算，就得到了一種叫做反向傳播的算法。

（2）用計算圖進行自動微分

思考反向傳播的一種有用方法是利用計算圖。計算圖是TensorFlow和深度學(xué)習(xí)革命的核心數(shù)據(jù)結(jié)構(gòu)。它是一種由運算構(gòu)成的有向無環(huán)圖。如今，現(xiàn)代框架比如TensorFlow，支持基于計算圖的自動微分，可以計算任意可維張量運算組合的梯度，只需寫出前向傳播，而無需做任何額外工作。

GradientTape是一個API，讓你可以充分利用TensorFlow強大的自動微分能力。它是一個Python作用域，能夠以計算圖（tape）的形式記錄在其中運行的張量運算。

3、實踐：使用Python的Kears庫識別手寫數(shù)字

在這個例子中，我們要解決的問題是，將手寫數(shù)字的灰度圖像（28像素 * 28像素）劃分到10個類別（從0到9）中，我們將使用MNIST數(shù)據(jù)集，它是機器學(xué)習(xí)領(lǐng)域的一個經(jīng)典數(shù)據(jù)集。你可以將解決MNIST問題看作深度學(xué)習(xí)的“Hello World”。

3.1 加載Kears中的MNIST數(shù)據(jù)集

from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images, train_labels組成了訓(xùn)練集，模型將從這些數(shù)據(jù)中進行學(xué)習(xí)。我們會在測試集test_images, test_labels上對模型進行測試。

查看數(shù)據(jù)集形狀：

>>> train_images.shape
(60000, 28, 28) //訓(xùn)練集為60000張圖片，每張圖片中28*28像素點數(shù)據(jù)
>>> test_images.shape
(10000, 28, 28) //測試集為10000張圖片，每張圖片中28*28像素點數(shù)據(jù)

3.2 神經(jīng)網(wǎng)絡(luò)架構(gòu)模型

from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
    layers.Dense(512, activation="relu"),
    layers.Dense(10, activation="softmax")
])

神經(jīng)網(wǎng)絡(luò)的核心組件是層（layer），大多數(shù)深度學(xué)習(xí)工作設(shè)計將簡單的層鏈接起來，從而實現(xiàn)漸進式的數(shù)據(jù)蒸餾，從輸入數(shù)據(jù)中提取表示。

本例中的模型包含2個Dense層，每層都對輸入數(shù)據(jù)做一些簡單的張量運算（relu、softmax），這些運算都涉及權(quán)重張量，權(quán)重張量是該層的屬性或參數(shù)，里面保存了模型所學(xué)到的知識。

3.3 模型編譯

model.compile(
    optimizer="rmsprop",
    loss="sparse_categorical_crossentropy",
    metrics=["accuracy"]
)

這里指定了編譯的3個步驟：優(yōu)化器、損失函數(shù)以及監(jiān)控的指標(biāo)。其中sparse_categorical_crossentropy是損失函數(shù)，用于學(xué)習(xí)權(quán)重張量的反饋信號；使用rmsprop優(yōu)化器，通過小批量隨機梯度下降（SGD）降低損失值。

3.4 準(zhǔn)備圖像數(shù)據(jù)

train_images = train_images.reshape((60000, 28*28))
train_images = train_images.astype("float32") / 255
test_images = test_images.reshape((10000, 28*28))
test_images = test_images.astype("float32") / 255

在開始訓(xùn)練之前，我們先對數(shù)據(jù)進行預(yù)處理，將其變化為模型要求的形狀，并縮放到所有值都在[0, 1]區(qū)間。

3.5 擬合模型

model.fit(train_images, train_labels, epochs=5, batch_size=128)

在Keras中通過調(diào)用模型的fit方法來完成訓(xùn)練數(shù)據(jù)上的擬合模型：模型開始在訓(xùn)練數(shù)據(jù)上進行迭代（每個小批量包含128個樣本），共迭代5輪。對于每批數(shù)據(jù)，模型會計算損失相對于權(quán)重的梯度，并將權(quán)重沿著減小該批量對應(yīng)損失值的方向移動，5輪迭代后訓(xùn)練精度到達了98.9%。

3.6 利用模型預(yù)測

>>> test_digits = test_images[0:10]
>>> predictions = model.predict(test_digits)
>>> predictions[0]
//為了方面閱讀，以下數(shù)據(jù)均為示例
array([1.07, 1.69, 6.13, 8.41, 2.99, 3.03, 8.36, 9.99, 2.66, 3.81], dtype=float32)

這個數(shù)組中的每個值，為對應(yīng)數(shù)字圖像test_digits[0]屬于0-9類別的概率，可以看到第7個概率最大，因此這個數(shù)字一定是7。檢查測試標(biāo)簽是否與之一致：

>>> test_lables[0]
7

3.7 在新數(shù)據(jù)上評估模型

>>> test_loss, test_acc = model.evaluate(test_images, test_lables)
>>> print(f"test_acc: {test_acc}")
test_acc: 0.9785

測試精度約為97.8%，比訓(xùn)練精度98.9%低不少。訓(xùn)練精度和測試精度之間的這種差距是過擬合造成的。

4、參考資料

圖書：Python深度學(xué)習(xí)（第2版）

作者：[美]弗朗索瓦·肖萊 著 張亮 譯

鏈接：https://item.jd.com/13378515.html?

審核編輯 黃宇