控制系統整定是控制系統設計和運行中的一個重要環節。整定的目的是為了使控制系統達到預期的性能指標,如穩定性、快速性、準確性和魯棒性等。下面將從以下幾個方面對控制系統整定進行介紹:
- 控制系統整定的概念和重要性
控制系統整定是指根據控制系統的性能要求,選擇合適的控制規律和參數,使系統達到預期的性能指標。控制系統整定的重要性主要體現在以下幾個方面:
1.1 提高系統的穩定性
穩定性是控制系統最基本的要求之一。通過整定,可以保證系統在受到擾動或參數變化時,能夠保持穩定運行,避免出現發散或振蕩現象。
1.2 改善系統的動態性能
動態性能是控制系統在響應輸入信號或擾動時,系統輸出的變化速度和幅度。通過整定,可以優化系統的動態性能,如減小超調、縮短調節時間等。
1.3 提高系統的準確性
準確性是指控制系統輸出與期望值之間的誤差大小。通過整定,可以減小系統的穩態誤差,提高系統的控制精度。
1.4 增強系統的魯棒性
魯棒性是指控制系統在面對模型不確定性、參數變化和外部擾動時,仍能保持良好性能的能力。通過整定,可以提高系統的魯棒性,使其在各種工況下都能穩定運行。
- 控制系統整定的方法
控制系統整定的方法有很多,主要包括以下幾種:
2.1 基于時域分析的整定方法
時域分析是一種基于系統時間響應的方法,通過分析系統的階躍響應、脈沖響應等,來確定控制規律和參數。常見的時域整定方法有:
PID控制器是一種常用的控制規律,通過調整比例系數、積分系數和微分系數,可以實現對系統性能的優化。常見的PID整定方法有Ziegler-Nichols方法、Cohen-Coon方法等。
2.1.2 基于Bode圖的整定方法
Bode圖是一種頻域分析方法,通過分析系統的頻率響應,可以確定控制器的參數。常見的基于Bode圖的整定方法有伯德圖法、奈奎斯特法等。
2.2 基于頻域分析的整定方法
頻域分析是一種基于系統頻率響應的方法,通過分析系統的幅頻特性和相頻特性,來確定控制規律和參數。常見的頻域整定方法有:
2.2.1 基于奈奎斯特判據的整定方法
奈奎斯特判據是一種基于系統開環頻率響應的方法,通過分析系統的奈奎斯特圖,可以確定系統的穩定性和性能指標。
2.2.2 基于伯德圖的整定方法
伯德圖是一種頻域分析方法,通過分析系統的幅頻特性和相頻特性,可以確定控制器的參數。常見的基于伯德圖的整定方法有伯德圖法、伯德-奈奎斯特法等。
2.3 基于優化的整定方法
優化整定方法是一種基于數學優化的方法,通過建立目標函數和約束條件,利用優化算法求解控制器參數。常見的優化整定方法有:
2.3.1 線性二次調節器(LQR)方法
LQR方法是一種基于最小化性能指標的方法,通過求解線性二次最優控制問題,可以得到最優的控制器參數。
2.3.2 遺傳算法(GA)方法
遺傳算法是一種基于自然選擇和遺傳機制的優化方法,通過模擬生物進化過程,可以求解復雜的非線性優化問題。
- 控制系統整定的步驟
控制系統整定的步驟主要包括以下幾個方面:
3.1 確定性能指標
根據實際工程需求,確定控制系統的性能指標,如穩定性、快速性、準確性和魯棒性等。
3.2 建立數學模型
根據實際系統的特點,建立控制系統的數學模型,如傳遞函數、狀態空間模型等。
3.3 選擇控制規律
根據系統的特點和性能要求,選擇合適的控制規律,如PID控制、自適應控制、預測控制等。
3.4 確定初始參數
根據經驗和初步分析,確定控制器的初始參數,為后續的整定提供參考。
3.5 進行參數整定
利用整定方法,對控制器參數進行調整和優化,直到滿足性能指標要求。
3.6 驗證和測試
在實際系統中應用整定后的控制器,進行驗證和測試,確保控制系統的性能達到預期要求。
-
控制系統
+關注
關注
41文章
6550瀏覽量
110498 -
PID
+關注
關注
35文章
1471瀏覽量
85306 -
參數
+關注
關注
11文章
1791瀏覽量
32110 -
輸入信號
+關注
關注
0文章
447瀏覽量
12542
發布評論請先 登錄
相關推薦
關于溫度控制的PID參數整定問題
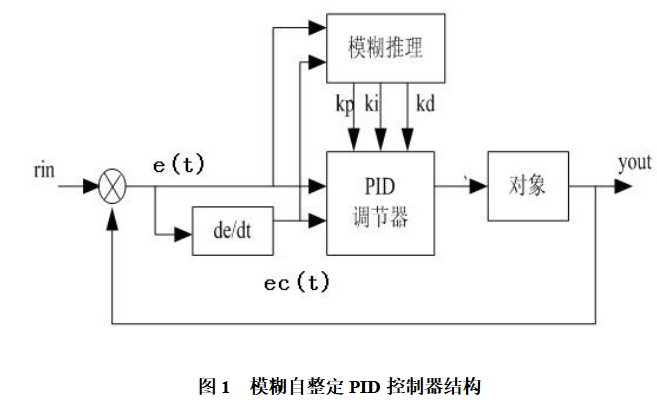
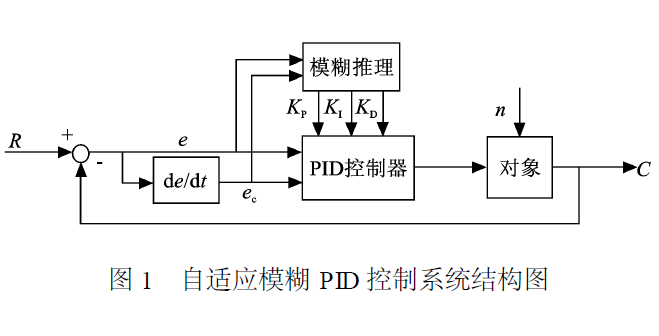
基于模糊自整定PID的主汽溫串級控制系統的設計
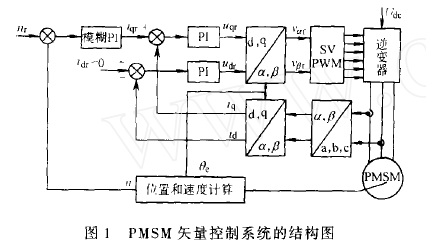
如何基于模糊推理的參數自整定PI控制器引入到PMSM矢量控制系統中
使用Matlab進行模糊自整定PID控制器系統的仿真分析




 為什么要對控制系統進行整定
為什么要對控制系統進行整定












評論