之前，論智曾在TOP 10：初學(xué)者需要掌握的10大機(jī)器學(xué)習(xí)（ML）算法介紹了一些基礎(chǔ)算法及其思路，為了與該帖聯(lián)動，我們特從機(jī)器學(xué)習(xí)熱門課程HSE的Introduction to Deep Learning和吳恩達(dá)的Neural Networks and Deep Learning中挑選了一些題目，演示Python、TensorFlow和Keras在深度學(xué)習(xí)中的實(shí)戰(zhàn)應(yīng)用.

如何建立一個(gè)線性分類器并進(jìn)行優(yōu)化.

在這個(gè)任務(wù)中，我們將實(shí)現(xiàn)一個(gè)線性分類器，并用numpy和隨機(jī)梯度下降算法對它進(jìn)行訓(xùn)練。

二元分類

為了更直觀，我們用人造數(shù)據(jù)（synthetic data）解決二元分類問題。

上圖中有紅、藍(lán)兩類數(shù)據(jù)，從分布上看它們不是線性可分的。所以為了分類，我們應(yīng)該在里面添加特征或使用非線性模型。請注意，圖中兩類數(shù)據(jù)的決策邊緣都呈圓形，這意味著我們能通過建立二元特征來使它們線性分離，具體思路如下圖所示：

用expand函數(shù)添加二次函數(shù)后，我們得到了這樣的測試結(jié)果：

1. # 簡單的隨機(jī)數(shù)測試

3. dummy_X = np.array([

4. [0,0],

5. [1,0],

6. [2.61,-1.28],

7. [-0.59,2.1]

8. ])

10. # 調(diào)用expand函數(shù)

11. dummy_expanded = expand(dummy_X)

13. # 它應(yīng)該返回這些值: x0 x1 x0^2 x1^2 x0*x1 1

14. dummy_expanded_ans = np.array([[0. , 0. , 0. , 0. , 0. , 1. ],

15. [1. , 0. , 1. , 0. , 0. , 1. ],

16. [2.61, -1.28, 6.8121, 1.6384, -3.3408, 1. ],

17. [-0.59, 2.1 , 0.3481, 4.41, -1.239, 1. ]])

logistic回歸

曾經(jīng)我們提到過，logistic回歸非常適合二元分類問題。為了分類對象，我們需要預(yù)測對象表示為1（默認(rèn)類）的概率，這就需要用到線性模型和邏輯函數(shù)的輸出：

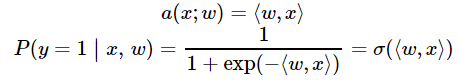
1. defprobability(X, w):

2. """

3. 對輸入賦值特征和權(quán)值

4. 根據(jù)上式，返回輸入x后y==1的預(yù)測概率，P(y=1|x)

6. :參數(shù) X: feature matrix X of shape [n_samples,6] (expanded) →特征矩陣X

7. :參數(shù) w: weight vector w of shape [6] for each of the expanded features →權(quán)值向量w

8. :返回值: 范圍在 [0,1] 之間的一系列概率.

9. """

11. return1./ (1+ np.exp(-np.dot(X, w)))

在logistic回歸中，我們能通過最小化交叉熵發(fā)現(xiàn)最優(yōu)參數(shù)w：

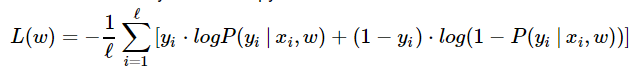
1. defcompute_loss(X, y, w):

2. """

3. 將特征矩陣X [n_samples,6], 目標(biāo)向量 [n_samples] of 1/0,

4. 以及權(quán)值向量 w [6]代入上述公式, 計(jì)算標(biāo)量的損失函數(shù).

5. """

6. return-np.mean(y*np.log(probability(X, w)) + (1-y)*np.log(1-probability(X, w)))

由于用了梯度下降算法訓(xùn)練模型，我們還需要計(jì)算梯度，具體來說，就是要對每個(gè)權(quán)值的損失函數(shù)求導(dǎo)：

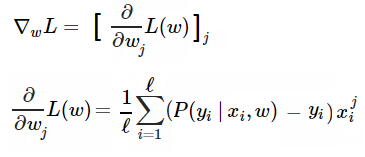
以下是具體的數(shù)學(xué)計(jì)算過程（也可點(diǎn)擊https://math.stackexchange.com/questions/477207/derivative-of-cost-function-for-logistic-regression/2539508#2539508查看）：

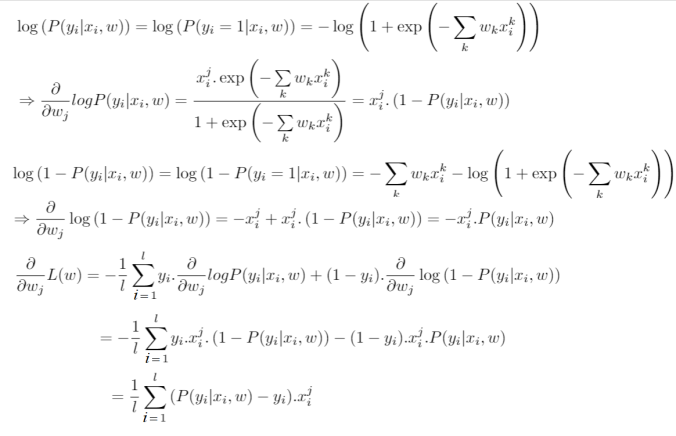
1. defcompute_grad(X, y, w):

2. """

3. 將特征矩陣X [n_samples,6], 目標(biāo)向量 [n_samples] of 1/0,

4. 以及權(quán)值向量 w [6]代入上述公式, 計(jì)算每個(gè)權(quán)值的導(dǎo)數(shù)vector [6].

5. """

7. returnnp.dot((probability(X, w) - y), X) / X.shape[0]

訓(xùn)練

現(xiàn)在我們已經(jīng)建立了函數(shù)，接下來就該用隨機(jī)梯度下降訓(xùn)練分類器了。我們將試著調(diào)試超參數(shù)，如batch size、學(xué)習(xí)率等，來獲得最佳設(shè)置。

Mini-batch SGD

不同于滿梯度下降，隨機(jī)梯度下降在每次迭代中只需要一個(gè)隨機(jī)樣本來計(jì)算其損失的梯度，并進(jìn)入下一個(gè)步驟：

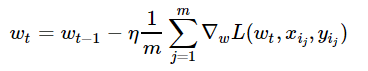
1. w = np.array([0,0,0,0,0,1])# 初始化

3. eta =0.05# 學(xué)習(xí)率

4. n_iter =100

5. batch_size =4

6. loss = np.zeros(n_iter)

8. foriinrange(n_iter):

9. ind = np.random.choice(X_expanded.shape[0], batch_size)

10. loss[i] = compute_loss(X_expanded, y, w)

11. dw = compute_grad(X_expanded[ind, :], y[ind], w)

12. w = w - eta*dw

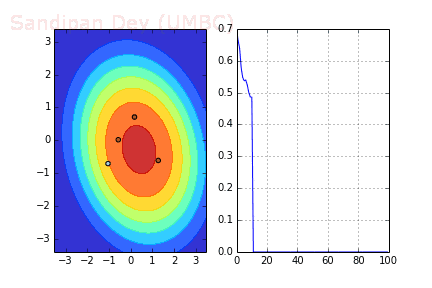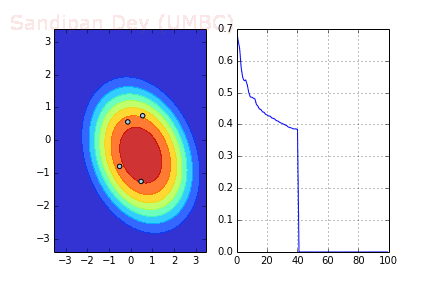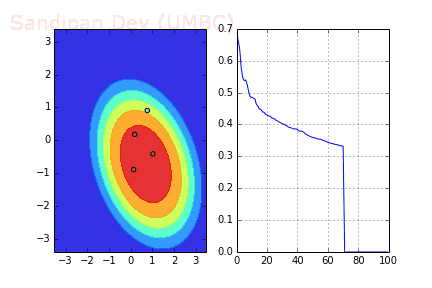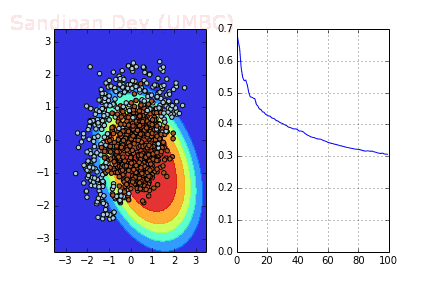
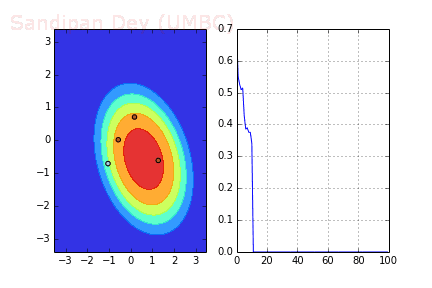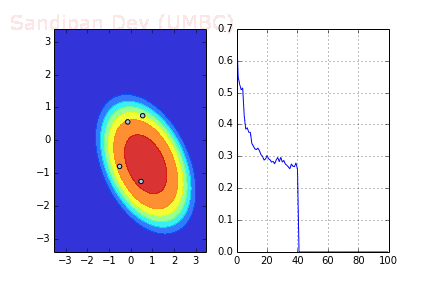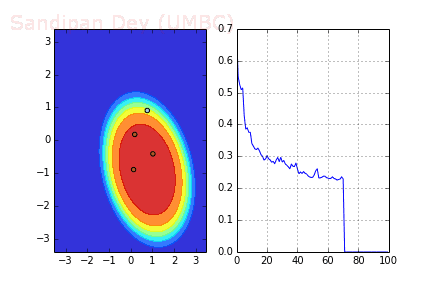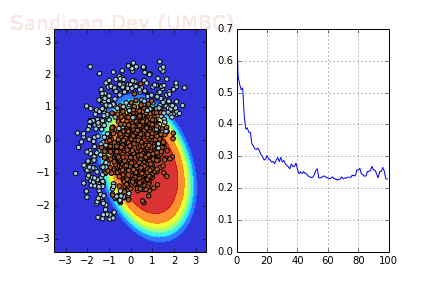
下圖展示了當(dāng)batch size=4時(shí)，決策面（decision surface）和交叉熵?fù)p失函數(shù)如何隨著不同batch的SGD發(fā)生變化。

用Momentum優(yōu)化SGD

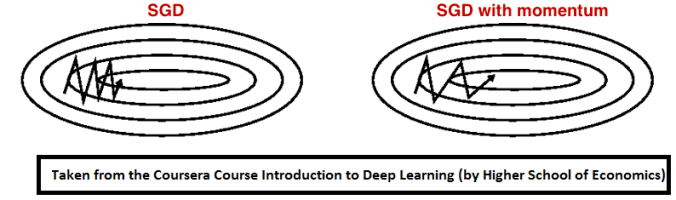
Momentum是模擬物理里動量的概念，如下圖所示，它能在相關(guān)方向加速SGD，抑制振蕩，從而加快收斂。從計(jì)算角度說，就是對上一步驟更新向量和當(dāng)前更新向量做加權(quán)平均，將其用于當(dāng)前計(jì)算。

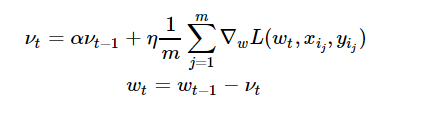
1. eta =0.05# 學(xué)習(xí)率

2. alpha =0.9# momentum

3. nu = np.zeros_like(w)

4. n_iter =100

5. batch_size =4

6. loss = np.zeros(n_iter)

8. foriinrange(n_iter):

9. ind = np.random.choice(X_expanded.shape[0], batch_size)

10. loss[i] = compute_loss(X_expanded, y, w)

11. dw = compute_grad(X_expanded[ind, :], y[ind], w)

12. nu = alpha*nu + eta*dw

13. w = w - nu

下圖展示了引入Momentum后，當(dāng)batch size=4時(shí)相應(yīng)決策面和交叉熵?fù)p失函數(shù)隨不同batch SGD+momentum發(fā)生的變化。可以看出，損失函數(shù)下降速度明顯加快，更快收斂。

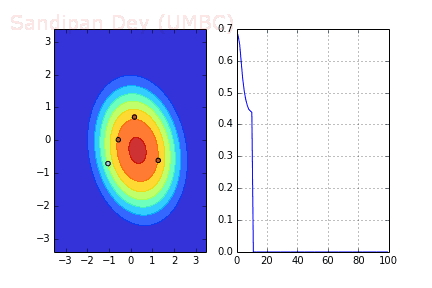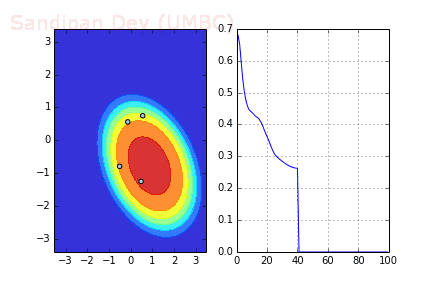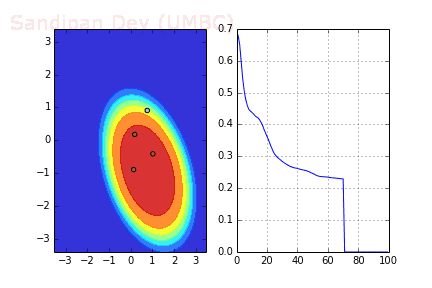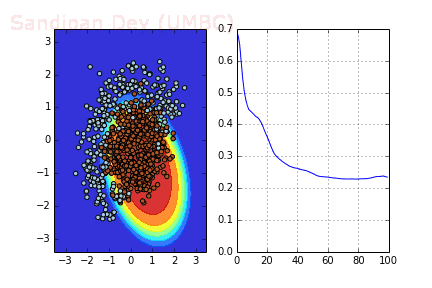
左：決策面；右：損失函數(shù)

RMSprop

加快收斂速度后，之后我們要做的是調(diào)整超參數(shù)學(xué)習(xí)率，這里我們介紹Hinton老爺子的RMSprop。這是一種十分高效的算法，利用梯度的平方來調(diào)整學(xué)習(xí)率：

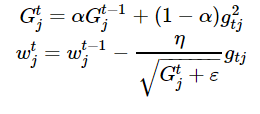
1. eta =0.05# 學(xué)習(xí)率

2. alpha =0.9# momentum

3. G = np.zeros_like(w)

4. eps =1e-8

5. n_iter =100

6. batch_size =4

7. loss = np.zeros(n_iter)

9. foriinrange(n_iter):

10. ind = np.random.choice(X_expanded.shape[0], batch_size)

11. loss[i] = compute_loss(X_expanded, y, w)

12. dw = compute_grad(X_expanded[ind, :], y[ind], w)

13. G = alpha*G + (1-alpha)*dw**2

14. w = w - eta*dw / np.sqrt(G + eps)

下圖是使用了SGD + RMSProp后決策面和損失函數(shù)的變化情況，較之之前，函數(shù)下降更快，收斂也更快。