我對圖像處理一直很感興趣，曾經寫過好幾篇博客。

前幾天讀到一篇文章，它提到圖像其實是一種波，可以用波的算法處理圖像。我頓時有一種醍醐灌頂的感覺，從沒想到這兩個領域是相關的，圖像還可以這樣玩！下面我就來詳細介紹這篇文章。

一、為什么圖像是波？

我們知道，圖像由像素組成。下圖是一張 400 x 400 的圖片，一共包含了 16 萬個像素點。

每個像素的顏色，可以用紅、綠、藍、透明度四個值描述，大小范圍都是0 ～ 255，比如黑色是[0, 0, 0, 255]，白色是[255, 255, 255, 255]。通過Canvas API就可以拿到這些值。

如果把每一行所有像素（上例是400個）的紅、綠、藍的值，依次畫成三條曲線，就得到了下面的圖形。

可以看到，每條曲線都在不停的上下波動。有些區域的波動比較小，有些區域突然出現了大幅波動（比如 54 和 324 這兩點）。

對比一下圖像就能發現，曲線波動較大的地方，也是圖像出現突變的地方。

這說明波動與圖像是緊密關聯的。圖像本質上就是各種色彩波的疊加。

二、頻率

綜上所述，圖像就是色彩的波動：波動大，就是色彩急劇變化；波動小，就是色彩平滑過渡。因此，波的各種指標可以用來描述圖像。

頻率（frequency）是波動快慢的指標，單位時間內波動次數越多，頻率越高，反之越低。

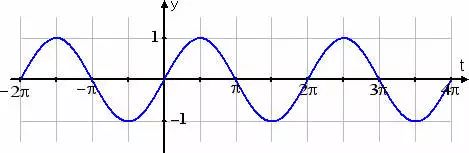
上圖是函數sin(Θ)的圖形，在2π的周期內完成了一次波動，頻率就是1。

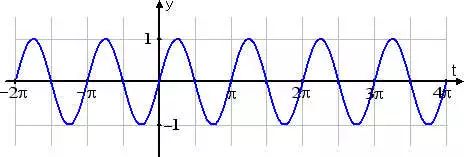
上圖是函數sin(2Θ)的圖形，在2π的周期內完成了兩次波動，頻率就是2。

所以，色彩劇烈變化的地方，就是圖像的高頻區域；色彩穩定平滑的地方，就是低頻區域。

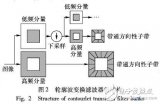
三、濾波器

物理學對波的研究已經非常深入，提出了很多處理波的方法，其中就有濾波器（filter）：過濾掉某些波，保留另一些波。

下面是兩種常見的濾波器 。

低通濾波器（lowpass）：減弱或阻隔高頻信號，保留低頻信號

高通濾波器（highpass）：減弱或阻隔低頻信號，保留高頻信號

下面是低通濾波的例子。

上圖中，藍線是原始的波形，綠線是低通濾波lowpass后的波形。可以看到，綠線的波動比藍線小很多，非常平滑。

下面是高通濾波的例子。

上圖中，黃線是原始的波形，藍線是高通濾波highpass后的波形。可以看到，黃線的三個波峰和兩個波谷（低頻波動），在藍線上都消失了，而黃線上那些密集的小幅波動（高頻波動），則是全部被藍線保留。

再看一個例子。

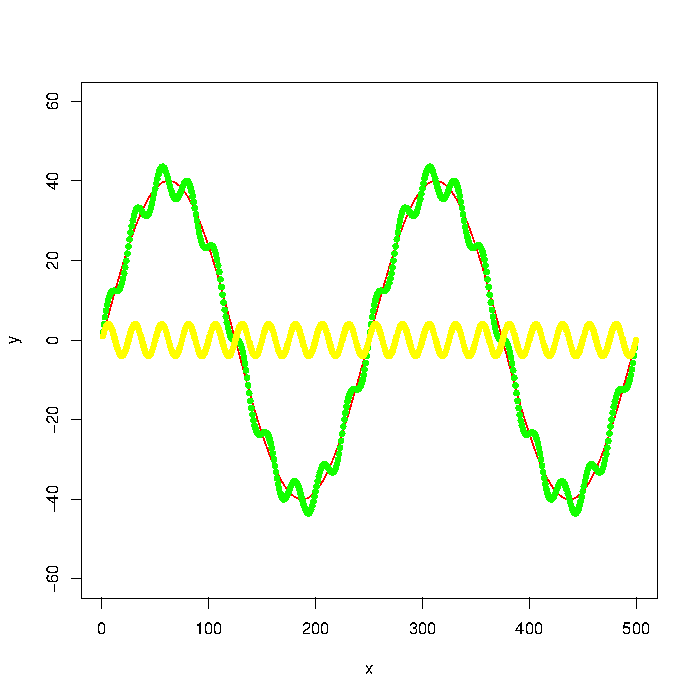
上圖有三根曲線，黃線是高頻波動，紅線是低頻波動。它們可以合成為一根曲線，就是綠線。

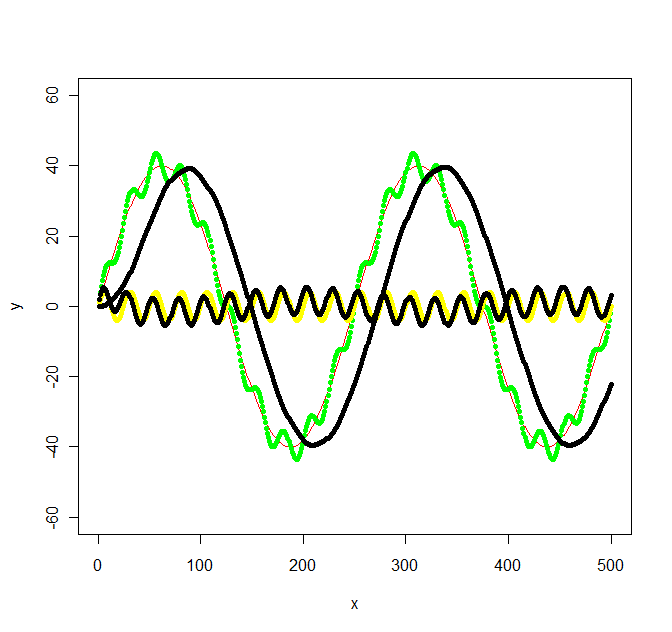
上圖中，綠線進行低通濾波和高通濾波后，得到兩根黑色的曲線，它們的波形跟原始的黃線和紅線是完全一致的。

四、圖像的濾波

瀏覽器實際上包含了濾波器的實現，因為Web Audio API里面定義了聲波的濾波。這意味著可以通過瀏覽器，將lowpass和highpass運用于圖像。

lowpass使得圖像的高頻區域變成低頻，即色彩變化劇烈的區域變得平滑，也就是出現模糊效果。

上圖中，紅線是原始的色彩曲線，藍線是低通濾波后的曲線。

highpass正好相反，過濾了低頻，只保留那些變化最快速最劇烈的區域，也就是圖像里面的物體邊緣，所以常用于邊緣識別。

上圖中，紅線是原始的色彩曲線，藍線是高通濾波后的曲線。

下面這個網址，可以將濾波器拖到圖像上，產生過濾后的效果。