引言
在全加器設(shè)計(jì)中運(yùn)用PG邏輯是非常普遍的,本文在設(shè)計(jì)和研究全加器時(shí),根據(jù)現(xiàn)有的PG邏輯公式推導(dǎo)出了一種新的邏輯公式,并論證了兩者之間的等價(jià)關(guān)系。這一新的公式能夠指導(dǎo)全加器設(shè)計(jì)中的連線方式,靈活更改連線策略。本文將從基本原理開(kāi)始逐步引出該公式,對(duì)其進(jìn)行論證,并應(yīng)用于全加器設(shè)計(jì)中。
基本原理
N位全加器將{AN,……,A1}、{BN,……,B1}和進(jìn)位輸入Cin作為輸入,計(jì)算得到和{SN,……,S1}以及最高位的進(jìn)位輸出Cout(見(jiàn)圖1)。每一位得到的和與進(jìn)位輸出都直接受其上一位的影響,其進(jìn)位輸出也會(huì)影響下一位。最終,整個(gè)全加器的和與輸出都受進(jìn)位輸入Cin的影響。
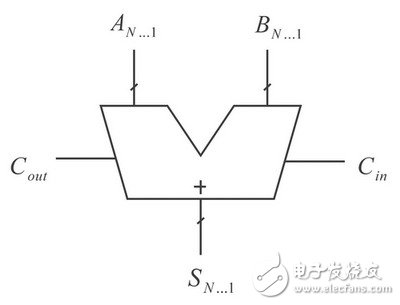
圖1 N位全加器
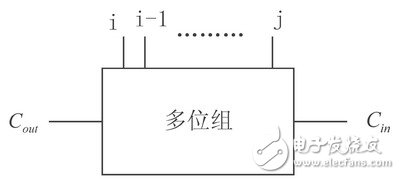
圖2 多位組傳播Cin 或者直接產(chǎn)生進(jìn)位輸出
全加器最簡(jiǎn)單的構(gòu)成方法就是把每一位的進(jìn)位輸出與下一位的進(jìn)位輸入簡(jiǎn)單地連接起來(lái),得到的就是行波進(jìn)位全加器。但在快速全加器中,是將加數(shù)和被加數(shù)中具有相同下標(biāo)的位分成若干組,即多個(gè)多位組,并將各個(gè)多位組看作一個(gè)整體。通過(guò)計(jì)算多位組的PG邏輯,在求和之前可預(yù)測(cè)多位組的進(jìn)位輸出是傳播進(jìn)位輸入還是直接產(chǎn)生進(jìn)位輸出。多位組所包括的位在i到j(luò)的范圍內(nèi)(見(jiàn)圖2),如果該多位組的進(jìn)位輸出是與進(jìn)位輸入無(wú)關(guān)的“真”值,那么它就產(chǎn)生了一個(gè)進(jìn)位;如果該多位組的進(jìn)位輸出只有當(dāng)進(jìn)位輸入為“真”時(shí)才進(jìn)位輸出“真”值,那么它就傳播了一個(gè)進(jìn)位。對(duì)于i≥k≥j,這些信號(hào)能夠遞歸地定義為:
Gi:j=Gi:k+Pi:kGk-1:j;Pi:j=Pi:kPk-1:j
其中 Gi:i≡Gi=AiBi;Pi:i≡Pi=Aii;定義 G0:0=Cin;P0:0=0
通過(guò)觀察可知,第i位的進(jìn)位輸出總是與Cin有關(guān),所以有Ci=Ci:0,和Si=Ai臖i臗i-1=Pii臛i-1:0。由此可見(jiàn),只要算出各位的Pi:i值和Gi:0值,就可以將各位的Si值求出。而其中最關(guān)鍵的就是利用遞歸公式快速算出各Gi:0值。上述遞歸表達(dá)式可以用如圖3所示的電路表示。
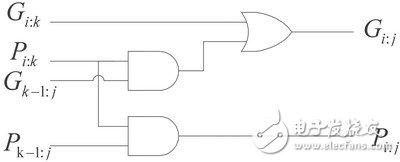
圖3 遞歸表達(dá)式的對(duì)應(yīng)電路
為了能夠更加簡(jiǎn)潔地表達(dá)全加器電路結(jié)構(gòu),可將圖3中的電路用圖4所示的黑色單元表示,并用圖4中的白色單元表示圖5所示的G邏輯產(chǎn)生電路。
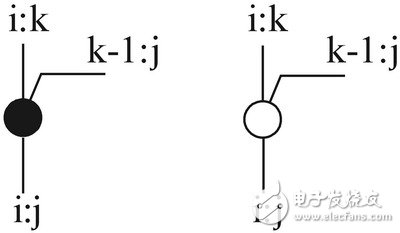
圖4 黑色單元和白色單元
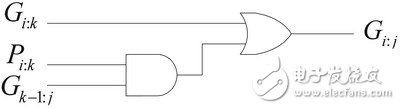
圖5 G邏輯產(chǎn)生電路
根據(jù)遞歸公式,可以得到各種不同結(jié)構(gòu)的全加器,他們的邏輯級(jí)數(shù)、扇出、布線通道數(shù)、所用單元數(shù)等各不相同,在此不再贅述,只給出一種Kogge-Stone樹(shù)型全加器PG網(wǎng)絡(luò),如圖6所示。圖的上部即是各位的本位Pi:i和Gi:i產(chǎn)生邏輯,中部是PG傳播網(wǎng)絡(luò),下部是各位的進(jìn)位輸出Ci。這種樹(shù)型全加器具有理想的邏輯級(jí)數(shù)和扇出,但是連線復(fù)雜,也需要更多的單元。
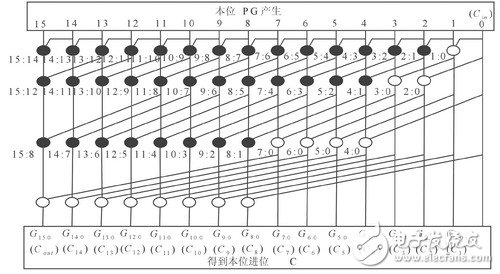
圖6 Kogge-Stone樹(shù)型全加器PG網(wǎng)絡(luò)
等價(jià)型PG邏輯的論證
對(duì)上文給出的遞歸表達(dá)式進(jìn)行進(jìn)一步推導(dǎo),可得出如下結(jié)果:Gi:j=Gi:k+Pi:kGk-1:j=Gi:k+Pi:kGk:j(Gk-1:j可用Gk:j替代)
下面給出它的簡(jiǎn)單推導(dǎo)過(guò)程:
因?yàn)椋珿k:j=Gk:k+Pk:kGk-1:j
所以,Gi:k+Pi:kGk:j=Gi:k+Pi:k(Gk:k+Pk:kGk-1:j)=Gi:k+Pi:kGk:k+Pi:kPk:kGk-1:j
將Gi:k展開(kāi)以后,上式=Gi:k+1+Pi:k+1Gk:k+Pi:kGk:k+Pi:kPk:k Gk-1:j
因?yàn)椋琍i:k=Pi:k+1Pk:k=Pi:kPk:k
所以,上式
=Gi:k+1+Pi:k+1Gk:k(1+Pk:k)+Pi:kGk-1:j
=Gi:k+1+Pi:k+1Gk:k+Pi:kGk-1:j
=Gi:k+1+Pi:kGk-1:j
=Gi:j
等價(jià)型PG邏輯的運(yùn)用
運(yùn)用新推導(dǎo)的等價(jià)型PG邏輯,可以改變PG傳播網(wǎng)絡(luò)的連接形式,如圖7所示,原來(lái)某些應(yīng)該獨(dú)立連接的節(jié)點(diǎn),現(xiàn)在可以利用等價(jià)型邏輯表達(dá)式將它們連在一起,比如在圖7中的“5:4”和“4:3”兩個(gè)節(jié)點(diǎn),在圖6中它們分別應(yīng)該按原始公式連接“3:2”和“2:1”兩點(diǎn),現(xiàn)在可以根據(jù)新公式將它們都連接到“3:2”,其它節(jié)點(diǎn)以此類(lèi)推。而且,在圖7中的“3:0”節(jié)點(diǎn)處負(fù)載較重,因此可以將“11:4”、“10:4”連接到“4:0”,以減輕“3:0”處的負(fù)載。總的說(shuō)來(lái),改進(jìn)以后的全加器在布線上可以相對(duì)于未改進(jìn)的電路減少近一半,但負(fù)載相對(duì)來(lái)說(shuō)也增加了一倍。因此,在實(shí)際電路中可以靈活調(diào)整連接關(guān)系,以平衡布線與負(fù)載之間的矛盾,同時(shí)對(duì)某些負(fù)載重的節(jié)點(diǎn)需要增加若干反相器,以增大該節(jié)點(diǎn)的驅(qū)動(dòng)能力。
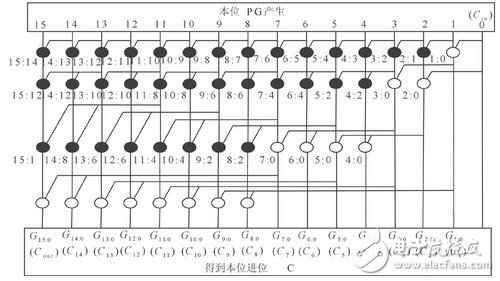
圖8 改進(jìn)PG傳播網(wǎng)絡(luò)以后的全加器
仿真與驗(yàn)證
本文按照等價(jià)型PG邏輯的原理編寫(xiě)了如上所述的15位加法器的Verilog描述,并用ModelSim對(duì)其進(jìn)行了仿真,對(duì)隨機(jī)數(shù)進(jìn)行相加,得到了正確的結(jié)果,說(shuō)明在邏輯上該P(yáng)G邏輯是正確的,如圖8所示。其中a、b為兩個(gè)15位的隨機(jī)數(shù),ci為隨機(jī)的進(jìn)位輸入,co為進(jìn)位輸出,sum是最終的和(其最高位是co)。
圖8 運(yùn)用等價(jià)型PG邏輯設(shè)計(jì)的15位加法器的仿真波形
結(jié)語(yǔ)
本文根據(jù)現(xiàn)有PG邏輯計(jì)算公式,推導(dǎo)出了一種新的與之等價(jià)的邏輯表達(dá)式。將這一邏輯表達(dá)式運(yùn)用到加法器設(shè)計(jì)中去,能夠改變PG傳播網(wǎng)絡(luò)的結(jié)構(gòu),減少連線數(shù)目,降低布線復(fù)雜度,這樣會(huì)更有利于后端的版圖布線。但此方法會(huì)相應(yīng)增大某些節(jié)點(diǎn)的負(fù)載,勢(shì)必帶來(lái)延遲的增加,因此需要精心設(shè)計(jì)晶體管尺寸或增加節(jié)點(diǎn)處的驅(qū)動(dòng)能力,以使電路達(dá)到時(shí)序要求。
在今后的全加器設(shè)計(jì)中,可以根據(jù)具體情況靈活調(diào)整PG傳播網(wǎng)絡(luò)的結(jié)構(gòu),盡量使得布線與負(fù)載達(dá)到一定程度的平衡。
-
負(fù)載
+關(guān)注
關(guān)注
2文章
560瀏覽量
34241 -
全加器
+關(guān)注
關(guān)注
10文章
62瀏覽量
28453
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
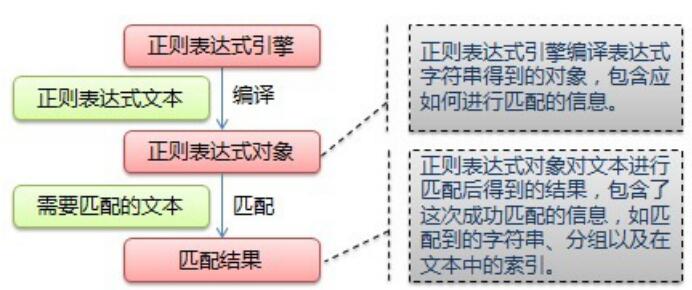
什么是正則表達(dá)式?正則表達(dá)式如何工作?哪些語(yǔ)法規(guī)則適用正則表達(dá)式?
MATLAB符號(hào)表達(dá)式
邏輯表達(dá)式的簡(jiǎn)化和轉(zhuǎn)換方法的改進(jìn)
防范表達(dá)式的失控
OFDM的基帶信號(hào)表達(dá)式

Python正則表達(dá)式指南
基于運(yùn)算符信息的數(shù)學(xué)表達(dá)式檢索技術(shù)
Lambda表達(dá)式詳解
表達(dá)式與邏輯門(mén)之間的關(guān)系
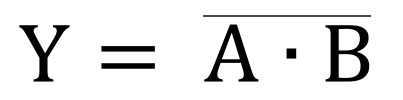
C語(yǔ)言的表達(dá)式

邏輯運(yùn)算符與表達(dá)式

位邏輯運(yùn)算符與表達(dá)式





 改變?cè)腥悠鹘Y(jié)構(gòu)的等價(jià)型邏輯表達(dá)式
改變?cè)腥悠鹘Y(jié)構(gòu)的等價(jià)型邏輯表達(dá)式










評(píng)論