背景
AVL 樹是一棵平衡的二叉查找樹,于 1962 年,G. M. Adelson-Velsky 和 E. M. Landis 在他們的論文《An algorithm for the organization of information》中發表。
所謂的平衡之意,就是樹中任意一個結點下左右兩個子樹的高度差不超過 1。(本文對于樹的高度約定為:空結點高度是 0,葉子結點高度是 1。)

那 AVL 樹和普通的二叉查找樹有何區別呢?如圖,如果我們插入的是一組有序上升或下降的數據,則一棵普通的二叉查找樹必然會退化成一個單鏈表,其查找效率就降為 O(n)。而 AVL 樹因其平衡的限制,可以始終保持 O(logn) 的時間復雜度。
具體實現與代碼分析
在我們進行完插入或刪除操作后,很可能會導致某個結點失去平衡,那么我們就需要把失衡結點旋轉一下,使其重新恢復平衡。
經過分析,不管是插入還是刪除,它們都會有四種失衡的情況:左左失衡,右右失衡,左右失衡,右左失衡。因此每次遇到失衡時,我們只需判斷一下是哪個失衡,再對其進行相對應的恢復平衡操作即可。
好,下面以插入操作為例,來看下這四種失衡的廬山真面目。(以下統一約定:紅色結點為新插入結點,y 結點為失衡結點)
(1)左左失衡
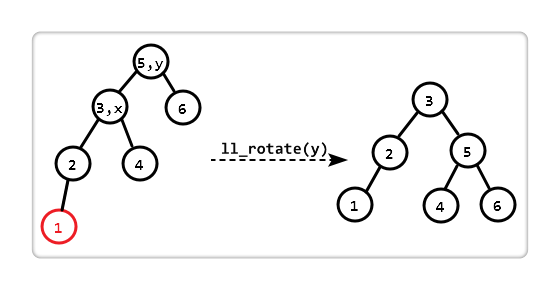
所謂的左左,即 "失衡結點" 的左子樹比右子樹高 2,左孩子下的左子樹比右子樹高 1。
我們只需對 "以 y 為根的子樹" 進行 "左左旋轉 (ll_rotate)" 即可。一次旋轉后,恢復平衡。
Node * AVL::ll_rotate(Node * y)
{
Node * x = y->left;
y->left = x->right;
x->right = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x;
}
(2)右右失衡

所謂的右右,即 "失衡結點" 的右子樹比左子樹高 2,右孩子下的右子樹比左子樹高 1。
我們只需對 "以 y 為根的子樹" 進行 "右右旋轉 (rr_rotate)" 即可。一次旋轉后,恢復平衡。
Node * AVL::rr_rotate(Node * y)
{
Node * x = y->right;
y->right = x->left;
x->left = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x;
}
(3)左右失衡

所謂的左右,即 "失衡結點" 的左子樹比右子樹高 2,左孩子下的右子樹比左子樹高 1。
觀察發現,若先對 "以 x 為根的子樹" 進行 "右右旋轉 (rr_rotate)",此時 "以 y 為根的子樹" 恰好符合 "左左失衡",所以再進行一次 "左左旋轉 (ll_rotate)"。兩次旋轉后,恢復平衡。
Node * AVL::lr_rotate(Node * y)
{
Node * x = y->left;
y->left = rr_rotate(x);
return ll_rotate(y);
}
(4)右左失衡
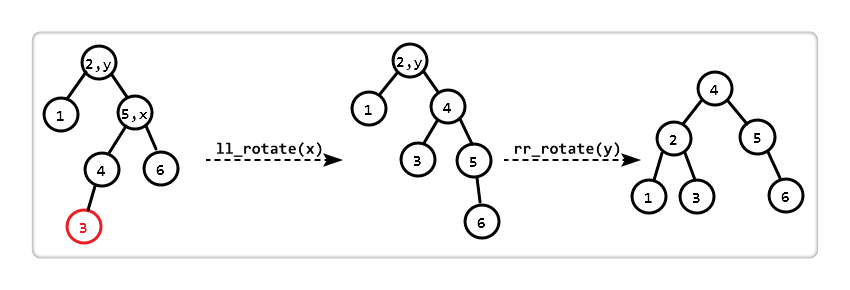
所謂的右左,即 "失衡結點" 的右子樹比左子樹高 2,右孩子下的左子樹比右子樹高 1。
觀察發現,若先對 "以 x 為根的子樹" 進行 "左左旋轉 (ll_rotate)",此時 "以 y 為根的子樹" 恰好符合 "右右失衡",所以再進行一次 "右右旋轉 (rr_rotate)"。兩次旋轉后,恢復平衡。
Node * AVL::rl_rotate(Node * y)
{
Node * x = y->right;
y->right = ll_rotate(x);
return rr_rotate(y);
}
插入操作
插入成功后,在遞歸回溯時依次對經過的結點判斷是否失衡,若失衡就需要對其進行對應的旋轉操作使其恢復平衡,在這期間,原先作為一棵子樹的根結點就會因為旋轉被替換,因此設置insert_real( )返回的是新根結點,這樣就可以實時更新根結點。
插入操作實現代碼如下:
int AVL::get_height(Node * node)
{
if (node == nullptr)
return 0;
return node->height;
}
int AVL::get_balance(Node * node)
{
if (node == nullptr)
return 0;
return get_height(node->left) - get_height(node->right);
}
Node * AVL::insert_real(int key, Node * node)
{
if (node == nullptr)
return new Node(key);
if (key < node->key)
node->left = insert_real(key, node->left);
else if (key > node->key)
node->right = insert_real(key, node->right);
else
return node;
node->height = max(get_height(node->left), get_height(node->right)) + 1;
int balance = get_balance(node);
// 左左失衡
if (balance > 1 && get_balance(node->left) > 0)
return ll_rotate(node);
// 右右失衡
if (balance < -1 && get_balance(node->right) < 0)
return rr_rotate(node);
// 左右失衡
if (balance > 1 && get_balance(node->left) < 0)
return lr_rotate(node);
// 右左失衡
if (balance < -1 && get_balance(node->right) > 0)
return rl_rotate(node);
return node;
}
void AVL::insert(int key)
{
header->left = insert_real(key, header->left);
}
查找操作
Node * AVL::find_real(int key, Node * node)
{
if (node == nullptr)
return nullptr;
if (key < node->key)
return find_real(key, node->left);
else if (key > node->key)
return find_real(key, node->right);
else
return node;
}
Node * AVL::find(int key)
{
return find_real(key, header->left);
}
刪除操作
刪除操作的四種失衡情況和插入操作一樣,讀者可以參考前文。下面是刪除操作的實現代碼:
Node * AVL::erase_real(int key, Node * node)
{
if (node == nullptr)
return node;
if (key < node->key)
node->left = erase_real(key, node->left);
else if (key > node->key)
node->right = erase_real(key, node->right);
else
{
if (node->left && node->right)
{
// 找到后繼結點
Node * x = node->right;
while (x->left)
x = x->left;
// 后繼直接復制
node->key = x->key;
// 轉化為刪除后繼
node->right = erase_real(x->key, node->right);
}
else
{
Node * t = node;
node = node->left ? node->left : node->right;
delete t;
if (node == nullptr)
return nullptr;
}
}
node->height = max(get_height(node->left), get_height(node->right)) + 1;
int balance = get_balance(node);
// 左左失衡
if (balance > 1 && get_balance(node->left) >= 0) // 需要加等號
return ll_rotate(node);
// 右右失衡
if (balance < -1 && get_balance(node->right) <= 0) // 需要加等號
return rr_rotate(node);
// 左右失衡
if (balance > 1 && get_balance(node->left) < 0)
return lr_rotate(node);
// 右左失衡
if (balance < -1 && get_balance(node->right) > 0)
return rl_rotate(node);
return node;
}
void AVL::erase(int key)
{
header->left = erase_real(key, header->left);
}
完整代碼
/**
*
* author : 劉毅(Limer)
* date : 2017-08-17
* mode : C++
*/
#include
#include
using namespace std;
struct Node
{
int key;
int height;
Node * left;
Node * right;
Node(int key = 0)
{
this->key = key;
this->height = 1;
this->left = this->right = nullptr;
}
};
class AVL
{
private:
Node * header;
private:
Node * ll_rotate(Node * y);
Node * rr_rotate(Node * y);
Node * lr_rotate(Node * y);
Node * rl_rotate(Node * y);
void destroy(Node * node);
int get_height(Node * node);
int get_balance(Node * node);
Node * insert_real(int key, Node * node);
Node * find_real(int key, Node * node);
Node * erase_real(int key, Node * node);
void in_order(Node * node);
public:
AVL();
~AVL();
void insert(int key);
Node * find(int key);
void erase(int key);
void print();
};
Node * AVL::ll_rotate(Node * y)
{
Node * x = y->left;
y->left = x->right;
x->right = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x;
}
Node * AVL::rr_rotate(Node * y)
{
Node * x = y->right;
y->right = x->left;
x->left = y;
y->height = max(get_height(y->left), get_height(y->right)) + 1;
x->height = max(get_height(x->left), get_height(x->right)) + 1;
return x;
}
Node * AVL::lr_rotate(Node * y)
{
Node * x = y->left;
y->left = rr_rotate(x);
return ll_rotate(y);
}
Node * AVL::rl_rotate(Node * y)
{
Node * x = y->right;
y->right = ll_rotate(x);
return rr_rotate(y);
}
void AVL::destroy(Node * node)
{
if (node == nullptr)
return;
destroy(node->left);
destroy(node->right);
delete node;
}
int AVL::get_height(Node * node)
{
if (node == nullptr)
return 0;
return node->height;
}
int AVL::get_balance(Node * node)
{
if (node == nullptr)
return 0;
return get_height(node->left) - get_height(node->right);
}
Node * AVL::insert_real(int key, Node * node)
{
if (node == nullptr)
return new Node(key);
if (key < node->key)
node->left = insert_real(key, node->left);
else if (key > node->key)
node->right = insert_real(key, node->right);
else
return node;
node->height = max(get_height(node->left), get_height(node->right)) + 1;
int balance = get_balance(node);
// 左左失衡
if (balance > 1 && get_balance(node->left) > 0)
return ll_rotate(node);
// 右右失衡
if (balance < -1 && get_balance(node->right) < 0)
return rr_rotate(node);
// 左右失衡
if (balance > 1 && get_balance(node->left) < 0)
return lr_rotate(node);
// 右左失衡
if (balance < -1 && get_balance(node->right) > 0)
return rl_rotate(node);
return node;
}
Node * AVL::find_real(int key, Node * node)
{
if (node == nullptr)
return nullptr;
if (key < node->key)
return find_real(key, node->left);
else if (key > node->key)
return find_real(key, node->right);
else
return node;
}
Node * AVL::erase_real(int key, Node * node)
{
if (node == nullptr)
return node;
if (key < node->key)
node->left = erase_real(key, node->left);
else if (key > node->key)
node->right = erase_real(key, node->right);
else
{
if (node->left && node->right)
{
// 找到后繼結點
Node * x = node->right;
while (x->left)
x = x->left;
// 后繼直接復制
node->key = x->key;
// 轉化為刪除后繼
node->right = erase_real(x->key, node->right);
}
else
{
Node * t = node;
node = node->left ? node->left : node->right;
delete t;
if (node == nullptr)
return nullptr;
}
}
node->height = max(get_height(node->left), get_height(node->right)) + 1;
int balance = get_balance(node);
// 左左失衡
if (balance > 1 && get_balance(node->left) >= 0) // 需要加等號
return ll_rotate(node);
// 右右失衡
if (balance < -1 && get_balance(node->right) <= 0) // 需要加等號
return rr_rotate(node);
// 左右失衡
if (balance > 1 && get_balance(node->left) < 0)
return lr_rotate(node);
// 右左失衡
if (balance < -1 && get_balance(node->right) > 0)
return rl_rotate(node);
return node;
}
void AVL::in_order(Node * node)
{
if (node == nullptr)
return;
in_order(node->left);
cout << node->key << " ";
in_order(node->right);
}
AVL::AVL()
{
header = new Node(0);
}
AVL::~AVL()
{
destroy(header->left);
delete header;
header = nullptr;
}
void AVL::insert(int key)
{
header->left = insert_real(key, header->left);
}
Node * AVL::find(int key)
{
return find_real(key, header->left);
}
void AVL::erase(int key)
{
header->left = erase_real(key, header->left);
}
void AVL::print()
{
in_order(header->left);
cout << endl;
}
int main()
{
AVL avl;
// test "insert"
avl.insert(7);
avl.insert(2);
avl.insert(1); avl.insert(1);
avl.insert(5);
avl.insert(3);
avl.insert(6);
avl.insert(4);
avl.insert(9);
avl.insert(8);
avl.insert(11); avl.insert(11);
avl.insert(10);
avl.insert(12);
avl.print(); // 1 2 3 4 5 6 7 8 9 10 11 12
// test "find"
Node * p = nullptr;
cout << ((p = avl.find(2)) ? p->key : -1) << endl;? ?//? 2
cout << ((p = avl.find(100)) ? p->key : -1) << endl; // -1
// test "erase"
avl.erase(1);
avl.print(); // 2 3 4 5 6 7 8 9 10 11 12
avl.erase(9);
avl.print(); // 2 3 4 5 6 7 8 10 11 12
avl.erase(11);
avl.print(); // 2 3 4 5 6 7 8 10 12
return 0;
}
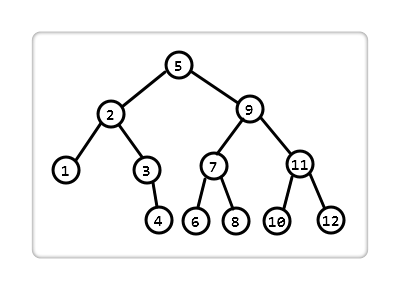
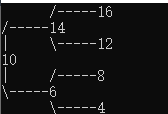
起初構造的 AVL 樹為下圖:
總結
和二叉查找樹相比,AVL 樹的特點是時間復雜度更穩定,但缺點也是很明顯的。
插入操作中,至多需要一次恢復平衡操作,遞歸回溯的量級為 O(logn)。有一點需要我們注意,在對第一個失衡結點進行恢復平衡后,遞歸回溯就應該立即停止(因為失衡結點的父親及其祖先們肯定都是處于平衡狀態的)。
但讓 "遞歸的回溯" 中途停止,不好實現,所以我上面的編碼程序都不可避免的會繼續回溯,直到整棵樹的根結點,而這些回溯都是沒有必要的。(謝謝 LLL 的提醒,若在結點中增設父親結點,就可以解決遞歸回溯的問題)
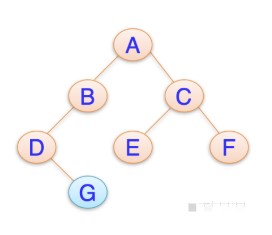
刪除操作中,若存在失衡,則至少需要一次恢復平衡操作,遞歸回溯的量級亦為 O(logn)。與插入操作不同,當對第一個失衡結點恢復平衡后,它的父親或者是它的祖先們也可能是非平衡的(見下圖,刪除 1),所以刪除操作的回溯很有必要。

沒有參照物對比的探討是沒有意義的,所以此文就止于此吧,有興趣的朋友可以看下我后面《紅黑樹》及《AVL 樹與紅黑樹的對比》的文章。
-
AVL
+關注
關注
0文章
14瀏覽量
10025 -
二叉樹
+關注
關注
0文章
74瀏覽量
12283
原文標題:一文讀懂 AVL 樹
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
二叉樹層次遍歷算法的驗證
紅黑樹(Red Black Tree)是一種自平衡的二叉搜索樹
二叉樹操作的相關知識和代碼詳解
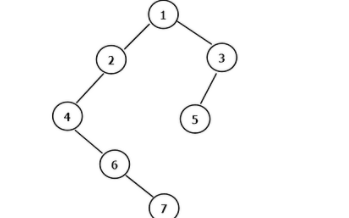




 AVL 樹和普通的二叉查找樹的詳細區別分析
AVL 樹和普通的二叉查找樹的詳細區別分析










評論