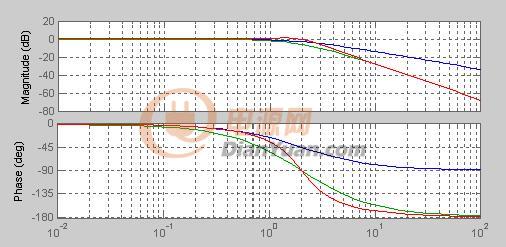
系統的頻率響應函數(Frequency Response Function, FRF)是描述線性時不變(Linear Time-Invariant, LTI)系統在不同頻率下輸入和輸出之間關系的數學工具。它是一個復數函數,通常用H(jω)表示,其中ω是角頻率,j是虛數單位。頻率響應函數可以提供系統在頻域內的行為特征,包括系統的增益、相位以及共振頻率等信息。
頻率響應函數與傳遞函數(Transfer Function, TF)有著密切的關系。傳遞函數是描述線性時不變系統輸入和輸出之間關系的復數函數,通常用H(s)表示,其中s是復頻率變量,可以表示為s = jω。傳遞函數是系統在頻域內的行為特征,它包含了系統的動態特性和穩態特性。
頻率響應函數和傳遞函數之間的關系可以通過以下步驟來理解:
- 拉普拉斯變換與傅里葉變換的關系
傳遞函數是通過拉普拉斯變換(Laplace Transform)得到的,而頻率響應函數是通過傅里葉變換(Fourier Transform)得到的。拉普拉斯變換是一種積分變換,可以處理時域信號的微分和積分,適用于描述系統的動態特性。傅里葉變換是一種線性變換,可以將時域信號轉換為頻域信號,適用于分析系統的頻域特性。
- 復頻率變量與角頻率的關系
傳遞函數中的復頻率變量s與頻率響應函數中的角頻率ω之間存在一定的關系。當s = jω時,傳遞函數H(s)可以表示為H(jω),即系統的頻率響應函數。這意味著,通過將傳遞函數中的復頻率變量s替換為jω,我們可以得到系統的頻率響應函數。
- 系統的穩態特性
傳遞函數可以描述系統的穩態特性,即系統在長時間內的行為。而頻率響應函數則可以提供系統在不同頻率下的穩態特性。通過分析頻率響應函數,我們可以了解系統在不同頻率下的增益和相位特性,從而判斷系統的穩定性和性能。
- 系統的動態特性
傳遞函數可以描述系統的動態特性,即系統在瞬態過程中的行為。而頻率響應函數則可以提供系統在不同頻率下的動態特性。通過分析頻率響應函數,我們可以了解系統在不同頻率下的共振頻率、阻尼比等信息,從而判斷系統的動態性能。
- 系統的濾波特性
傳遞函數可以描述系統的濾波特性,即系統對不同頻率信號的過濾效果。而頻率響應函數則可以提供系統在不同頻率下的濾波特性。通過分析頻率響應函數,我們可以了解系統對不同頻率信號的增益和相位特性,從而判斷系統的濾波性能。
- 系統的穩定性分析
傳遞函數可以用于系統的穩定性分析,即判斷系統是否在給定的輸入下保持穩定。而頻率響應函數則可以提供系統的穩定性信息。通過分析頻率響應函數,我們可以了解系統在不同頻率下的穩定性,從而判斷系統是否穩定。
- 系統的控制設計
傳遞函數在控制系統設計中具有重要應用,可以用于設計控制器以實現系統的穩定和性能要求。而頻率響應函數則可以提供系統的控制設計信息。通過分析頻率響應函數,我們可以了解系統在不同頻率下的控制性能,從而設計合適的控制器。
總之,系統的頻率響應函數是描述線性時不變系統在不同頻率下輸入和輸出之間關系的數學工具,它與傳遞函數有著密切的關系。
-
頻率響應
+關注
關注
1文章
101瀏覽量
18317 -
函數
+關注
關注
3文章
4308瀏覽量
62444 -
傅里葉變換
+關注
關注
6文章
438瀏覽量
42566
發布評論請先 登錄
相關推薦




 什么叫系統的頻率響應函數?它和傳遞函數有何關系
什么叫系統的頻率響應函數?它和傳遞函數有何關系
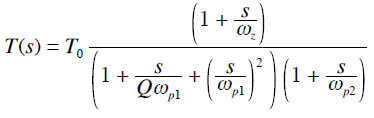
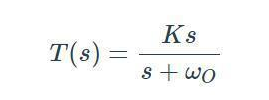










評論