在半導(dǎo)體中，除了能帶寬度外，一個重要的物理量是電荷載流子(電子和空穴)的遷移率。在本教程中，我們將研究霍爾效應(yīng)，這使我們能夠?qū)嶒炐缘卮_定半導(dǎo)體中的這一物理量。

電荷載流子遷移率

在本篇文章中，我們將采用在早期期刊中探討的德魯?shù)?洛倫茲框架。我們回顧一下，這一模型完全基于經(jīng)典力學(xué)。唯一的“外部”成分是電子的有效質(zhì)量m?;這是一種數(shù)學(xué)手段，使我們能夠?qū)㈦娮右暈椴皇芰Φ慕?jīng)典粒子。通過這種方式，我們避免了量子復(fù)雜性，因為我們需要考慮晶格離子施加的周期性勢能。極端總結(jié)如下場景：一個電子與一個離子發(fā)生非彈性碰撞，失去其所有的動能。

施加一個均勻的靜電場 E 會加速電子;加速度向量的大小為 a=m?eE?，其中 e 是電子電荷的絕對值。如果 τr? 是一次碰撞與下次碰撞之間的平均時間(弛豫時間)，則電子在經(jīng)歷新碰撞的瞬間速度向量的大小為 vd?=aτr?，其中我們識別出在前一篇文章中我們通過軟件重構(gòu)的漂移速度。轉(zhuǎn)向相應(yīng)的向量量(請記住在我們的符號中，電子電荷為 e<0，我們得到：

其中 n 是電子的數(shù)密度。電流密度向量 j 的方向與電場相同，而漂移速度則朝相反方向。從方程(1)中的歐姆定律可以推導(dǎo)出：

其中 σ 是電導(dǎo)率。

在室溫下，上述描述的場景再現(xiàn)了金屬的電氣行為。這些結(jié)果很容易擴(kuò)展到半導(dǎo)體，只要在 σ 的表達(dá)式中包含空穴的貢獻(xiàn)，其中空穴有一個有效質(zhì)量 ??mh??，通常與電子質(zhì)量不同。假設(shè)兩種電荷載流子的時間 τr? 相同是一種良好的近似(更復(fù)雜的模型則假設(shè) τr? 不僅依賴于載流子的符號，還依賴于單個電子/空穴)。

電導(dǎo)率的解析表達(dá)式通過定義電子和空穴的遷移率可以得到一個更易于處理的形式：

方程(3)從微觀角度定義了遷移率。考慮到上述公式，我們得出一種宏觀定義，即電荷載流子的遷移率是其漂移速度與電場的比值。從實驗的角度來看，量(3)可以通過霍爾效應(yīng)來確定。在進(jìn)入這個十九世紀(jì)發(fā)現(xiàn)的過程之前，我們必須澄清一些電磁學(xué)的概念。

磁場：B還是H

在關(guān)于電磁學(xué)的舊出版物中，假定 H(磁場強(qiáng)度)是基本向量，而 B(磁感應(yīng))是派生向量。然而，為了保持電量和磁量之間的對稱性，有必要將 B 視為基本向量。令人困惑的是，在靜電學(xué)中，電場強(qiáng)度 E 被視為基本向量，而電位移 D 是派生向量。

但在觀察麥克斯韋方程時，為了建立電荷與電流之間的對稱性，以及差分算子散度和旋度之間的對稱性，我們必須將 B 視為基本向量。在許多固態(tài)物理文獻(xiàn)中，H 出現(xiàn)在方程中，并說明該量與 B 相同，因為未考慮鐵磁材料。為了避免誤解，在我們的方程中，B 將作為磁場出現(xiàn)。

另一個問題是：“使用哪種單位制，國際單位制 (SI) 還是高斯單位制?”答案取決于讀者。如果他是物理學(xué)家，他會回答：“高斯”。如果他是工程師，他會回答：“國際單位制”。高斯單位制更適合亞原子過程，而 SI(或合理化的 MKS)則適用于宏觀系統(tǒng)。我們將使用 SI，其中 B 以 Wb/m2Wb/m2 為單位。

霍爾效應(yīng)

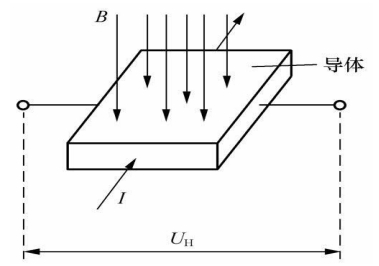
在霍爾效應(yīng)中，關(guān)鍵角色由洛倫茲力 F 負(fù)責(zé)，即作用于以速度 v 在磁場 B 中移動的電荷 q 的力。在國際單位制中：

我們考慮圖 1 中所示的實驗配置，在這個配置中，我們對一個具有平行六面體形狀的金屬導(dǎo)體的兩端施加一個恒定的電壓差 0V0?，其邊長為 L,d,w。在均勻和各向同性的條件下，將建立一個沿 y 軸方向的均勻靜電場：E=(0,E,0)。這導(dǎo)致電流密度 j 與電場向量 E 平行且一致，而速度向量則朝相反方向(如圖 1 中的虛線所示)。構(gòu)成導(dǎo)體的材料的均勻性和各向同性，加上熱平衡，保證了如上所述的直線軌跡。

激活一個均勻的磁靜場 B=(0,0,B) 產(chǎn)生一個洛倫茲力 F，其方向如圖 1 所示，偏轉(zhuǎn)單個電子的軌跡。由于導(dǎo)體的任何橫截面都是一個開路，因此電子無法無限流動。最終結(jié)果是在一個邊緣上出現(xiàn)負(fù)電荷的過剩(圖 1);隨后將建立一個名為霍爾場 EH? 的電場。更確切地說，當(dāng)霍爾場施加的力與洛倫茲力 F 相等且方向相反時，將達(dá)到平衡，如圖 1 中的力圖所示。通過速度向量與磁場正交，可以輕松展開表示洛倫茲力的向量積。

應(yīng)用動態(tài)平衡條件，我們可以輕松得到：EH?=vd?B，現(xiàn)在如果我們隨意選取導(dǎo)體的一個橫截面 ΣΣ，在點 1 和點 2 之間(圖 1)，將建立一個電壓差 VH?=EH?d(霍爾電壓)。考慮到 EH? 的表達(dá)式，并將 vd? 表示為電流密度 j 的函數(shù)，因此電流強(qiáng)度為 i=jS，其中 S=wd 是 ΣΣ 的面積，我們得到：

其中 RH?=ne1? 是霍爾系數(shù)，即電荷密度的倒數(shù)。考慮到(3)中的第一個公式，我們最終得到：

在方程(5)中，B 和 w 已知。量 VH? 和 i 可以被測量，因此我們可以計算 RH?;假設(shè)已知電導(dǎo)率 σ，(6)使我們能夠確定 μe?。不幸的是，對于金屬來說，由于電子數(shù)密度很高，VH? 太低;實際上，霍爾電壓與 RH? 成正比，即與電荷密度的倒數(shù)成正比。這在半導(dǎo)體中并不發(fā)生(此時電荷密度降低了大約 105105 倍)，注意到所獲得的結(jié)果很容易通過引入空穴的遷移率來擴(kuò)展。我們邀請讀者為一塊 p 型硅條確定空穴的遷移率，其條件為：

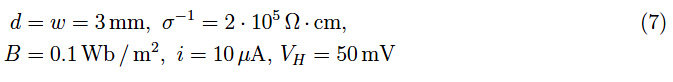
結(jié)論

所提出的實驗使我們能夠在室溫下確定遷移率。考慮極端溫度的模型更加復(fù)雜，例如在航天探測器上的半導(dǎo)體器件中發(fā)生的溫度。相反的極限(高溫)也是電力電子的一個典型問題。