哈密頓圖定義概念
哈密頓通路(回路)與哈密頓圖(Hamilton圖)通過圖G的每個結(jié)點一次,且僅一次的通路(回路),就是哈密頓通路(回路)。存在哈密頓回路的圖就是哈密頓圖。
1.哈密頓通路
設(shè)G=《V,E》為一圖(無向圖或有向圖).G中經(jīng)過每個頂點一次且僅一次的通路稱作哈密頓通路
2.哈密頓回路
G中經(jīng)過每個頂點一次且僅一次的回路稱作哈密頓回路
3.哈密頓圖
若G中存在哈密頓回路,則稱它是哈密頓圖
4.定義詳解:
(1)存在哈密頓通路(回路)的圖一定是連通圖;
(2)哈密頓通路是初級通路,哈密頓回路是初級回路;
(3)若G中存在哈密頓回路,則它一定存在哈密頓通路,反之不真
(4)只有哈密頓通路,無哈密頓回路的圖不交哈密頓圖;
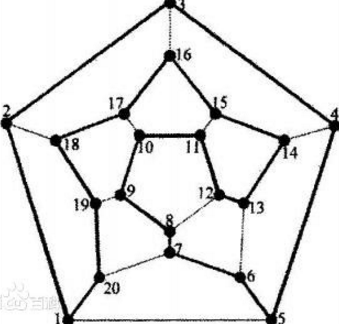
二、判定定理
注意:目前沒有找到哈密頓圖的簡單的充要條件
(1)設(shè)無向圖G=《V,E》為哈密頓圖,V1是V的任意真子集,則(注:n階xx圖指的是n個頂點,不要迷!)
p(G-V1)《=|V1|
其中,p(G-V1)為G中刪除V1后的所得圖的連通分支數(shù)目,|V1|為V1集合中包含的頂點個數(shù)。【哈密頓圖存在的必要條件】
推論:有割點的圖一定不是哈密頓圖
設(shè)v是圖中的割點,則p(G-v)》=2,由上述定理知G不是哈密頓圖
(2)設(shè)G是n(n》=3)階無向簡單圖,若對于G中的每一對不相鄰的頂點u,v,均有
d(u)+d(v)》=n-1
則G中存在哈密頓通路。又若
d(u)+d(v)》=n
則G中存在哈密頓回路,即G為哈密頓圖。【哈密頓圖存在的充分條件,不是必要條件】
其中d(u),d(v)分別代表頂點u,v的度數(shù)。
推論:設(shè)G是n(n》=3)階無向簡單圖,若G的最小度》=n/2,則G是哈密頓圖。
由推論知,對于完全圖Kn,當(dāng)n》=3時,是哈密頓圖,完全二部圖Kr,s當(dāng)r==s》=2時是哈密頓圖。
(3)在n(n》=2)階有向圖D=《V,E》中,如果略去所有有向邊的方向,所得無向圖中含生成子圖Kn,則D中存在哈密頓通路。
推論:n(n》=3)階有向完全圖是哈密頓圖。
1.常用方法判斷是哈密頓圖:
(1)若能通過觀察找出圖G中的一條哈密頓回路,則G當(dāng)然是哈密頓圖。
(2)若一個無向圖G滿足上述(2)中的條件,一個有向圖D滿足上述(3)的推論的條件,則G、D都是哈密頓圖。
2.破壞哈密頓圖存在的必要條件,判定不是哈密頓圖:
設(shè)n階圖G是哈密頓圖,則G應(yīng)該滿足以下諸條件:
(1)G必須是連通圖;
(2)G中的邊數(shù)m必須大于等于頂點數(shù)n;
(3)若G中存在2度頂點v,即d(v)=2,則與v關(guān)聯(lián)的兩條邊ei,ej必須在G中的任何哈密頓回路上;
(4)若G中存在每條哈密頓回路中出現(xiàn)的邊,不能構(gòu)成邊數(shù)小于n的初級回路(圈);
破壞以上諸條件中的一條,都不是哈密頓圖。
哈密頓回路的應(yīng)用
隨機生成并哈密頓回路求解:
// Graph.cpp : 定義控制臺應(yīng)用程序的入口點。
//
#include “stdafx.h”
#include“Graph.h”
#include《iostream》
#include《fstream》
#include《stack》
#include《queue》
#include《limits》
using namespace std;
template《class T,class E》
int sb(int start,Graph《T,E》 &myGraph,ostream & fout)//simple backtracking 算法解決圖的最小哈密頓回路問題 v為回路的起點和終點
{
E minDistance=std::numeric_limits《E》::max();
stack《int》 myStack;
myStack.push(start);
int numVertices=myGraph.NumberOfVertices();
bool *visited=new bool[numVertices];
memset(visited,false,numVertices);
int v;
int w=-1;
while(!myStack.empty()) //棧不為空
{
v=myStack.top();
visited[v]=true;
if(w==-1)
{
w=myGraph.getFirstNeighbor(v);
}
else
{
w=myGraph.getNextNeighbor(v,w);
}
for(;w!=-1&&visited[w]==true;w=myGraph.getNextNeighbor(v,w))
{
}
if(w==-1) //未找到可行的下一個頂點
{
myStack.pop(); //回溯
w=v;
visited[v]=false;
}
else //找到可行的下一個頂點
{
myStack.push(w); //放入棧中
if(myStack.size()==numVertices)//走過所有的頂點
{
if(myGraph.getWeight(start,w)==std::numeric_limits《E》::max()) //判斷最后一個頂點有沒有回到起點的邊
{
myStack.pop();
visited[w]=false;
}
else //成功找到回路
{
//輸出回路 并記錄下回路的長度
stack《int》 temp;
while(!myStack.empty())
{
int n=myStack.top();
temp.push(n);
myStack.pop();
}
fout《《“哈密頓回路 : ”;
E distance=0;
int n=temp.top();
myStack.push(n);
temp.pop();
int last=n;
fout《《n《《“--”;
while(!temp.empty())
{
n=temp.top();
myStack.push(n);
temp.pop();
distance+=myGraph.getWeight(last,n);
last=n;
fout《《n《《“--”;
}
fout《《start《《“--”《《endl;
distance+=myGraph.getWeight(last,start);
fout《《“總長度為:”《《distance《《endl;
//記錄最短長度
if(minDistance》distance)
{
minDistance=distance;
}
//
myStack.pop();
visited[w]=false;
}
}
else
{
w=-1;
}
}
}
fout《《“最短哈密頓回路的長度為:”《《minDistance《《endl;
return 1;
}
//分支限界法求解最短哈密頓回路問題
template《class E》
struct NODE
{
int dep; //表示該結(jié)點在搜索樹的第幾層
int *vertices; //該節(jié)點力包含的各個頂點
E length; //從根到當(dāng)前結(jié)點已經(jīng)走過的路徑長度
NODE(int depth)
{
dep=depth;
vertices=new int[dep];
};
void cpy(int *&des)
{
for(int i=0;i《dep;i++)
{
des[i]=vertices[i];
}
}
bool find(int v)
{
for(int i=0;i《dep;i++)
{
if(vertices[i]==v)
return true;
}
return false;
}
};
template《class T,class E》
int bb(int start,Graph《T,E》 & myGraph,ostream & fout)
{
stack《NODE《E》》 myStack; //隊列
E minDistance=std::numeric_limits《E》::max();
int s=myGraph.getFirstNeighbor(start);
for(s=myGraph.getNextNeighbor(start,s);s!=-1;s=myGraph.getNextNeighbor(start,s))
{
NODE《E》 n(2);
n.vertices[0]=start;n.vertices[1]=s;
n.length=myGraph.getWeight(start,s);
myStack.push(n);
}
while(!myStack.empty()) //隊列不為空
{
NODE《E》 n=myStack.top();
myStack.pop();
int v=n.vertices[n.dep-1];
if(n.dep+1==myGraph.NumberOfVertices())//到了最后一層 判斷是不是哈密頓回路
{
int w;
for( w=myGraph.getFirstNeighbor(v);w!=-1;w=myGraph.getNextNeighbor(v,w))
{
if( n.find(w)==false)
break;
}
if(w!=-1)
{
if(myGraph.getWeight(w,start)《std::numeric_limits《E》::max())
{
//形成回路
fout《《“哈密頓回路為:”;
for(int i=0;i《n.dep;i++)
{
fout《《n.vertices[i]《《“ ”;
}
fout《《w《《“ ”《《start《《endl;
E tempDistance=n.length+myGraph.getWeight(v,w)+myGraph.getWeight(w,start);
fout《《“總長度為: ”《《tempDistance《《endl;
if(minDistance》tempDistance)
{
minDistance=tempDistance;
}
}
}
}
for(int w=myGraph.getFirstNeighbor(v);w!=-1;w=myGraph.getNextNeighbor(v,w))
{
if(n.find(w)==false)
{
NODE《E》 ne(n.dep+1);
ne.length=n.length+myGraph.getWeight(v,w);
if(ne.length《minDistance)
{
n.cpy(ne.vertices);
ne.vertices[ne.dep-1]=w;
myStack.push(ne);
}
}
}
}
fout《《“最短長度為 ”《《minDistance《《endl;
return minDistance;
}
int _tmain(int argc, _TCHAR* argv[])
{
Graph《char,int》 myGraph(10);
//ifstream fin(“input.txt”);
//myGraph.Init(fin);
myGraph.RandInit();//隨機初始化圖
ofstream fout(“outputsb.txt”);
//sb(0,myGraph,fout);
ofstream fout1(“outputbb.txt”);
bb(0,myGraph,fout1);
system(“pause”);
return 0;
}
-
哈密頓圖
+關(guān)注
關(guān)注
0文章
3瀏覽量
1276
發(fā)布評論請先 登錄
相關(guān)推薦

DNA編碼的學(xué)習(xí)
電子關(guān)聯(lián)對聚乙炔雙激子態(tài)的影響
LaSrAlO4中Cu2+的自旋哈密頓參量的理論分析
ZigBee與哈密瓜不得不說的故事
哈密頓結(jié)構(gòu)修正的控制設(shè)計方法及其應(yīng)用
哈密頓回路算法
永磁同步直線電機位置控制
模擬量子計算的未來前景將一片光明
模擬量子計算有著優(yōu)異的表現(xiàn),未來將具有廣泛的應(yīng)用前景
模擬量子計算的實力前景不可限量
基于量子軟件的量子絕熱近似算法求解
基于量子材料的素描5d體系
基于高光譜的不同成熟期哈密瓜堅實度研究





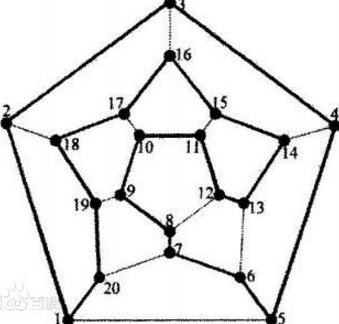
 哈密頓回路的應(yīng)用
哈密頓回路的應(yīng)用










評論