概念:
哈密頓圖:圖G的一個回路,若它通過圖的每一個節點一次,且僅一次,就是哈密頓回路。存在哈密頓回路的圖就是哈密頓圖。哈密頓圖就是從一點出發,經過所有的必須且只能一次,最終回到起點的路徑。圖中有的邊可以不經過,但是不會有邊被經過兩次。
與歐拉圖的區別:歐拉圖討論的實際上是圖上關于邊的可行便利問題,而哈密頓圖的要求與點有關。
判定:
一:Dirac定理(充分條件)
二:基本的必要條件
設圖G=《V, E》是哈密頓圖,則對于v的任意一個非空子集S,若以|S|表示S中元素的數目,G-S表示G中刪除了S中的點以及這些點所關聯的邊后得到的子圖,則W(G-S)《=|S|成立。其中W(G-S)是G-S中聯通分支數。
三:競賽圖(哈密頓通路)
N(N》=2)階競賽圖一點存在哈密頓通路。
算法:
一:在Dirac定理的前提下構造哈密頓回路
過程:
1:任意找兩個相鄰的節點S和T,在其基礎上擴展出一條盡量長的沒有重復結點的路徑。即如果S與結點v相鄰,而且v不在路徑S -》 T上,則可以把該路徑變成v -》 S -》 T,然后v成為新的S.從S和T分別向兩頭擴展,直到無法繼續擴展為止,即所有與S或T相鄰的節點都在路徑S -》 T上。
2:若S與T相鄰,則路徑S -》 T形成了一個回路。
3:若S與T不相鄰,可以構造出來一個回路。設路徑S -》 T上有k+2個節點,依次為S, v1, v2, 。。。, vk, T.可以證明存在節點vi(i屬于[1, k]),滿足vi與T相鄰,且vi+1與S相鄰。找到這個節點vi,把原路徑變成S -》 vi -》 T -》 vi+1 -》 S,即形成了一個回路。
4:到此為止,已經構造出來了一個沒有重復節點的的回路,如果其長度為N,則哈密頓回路就找到了。如果回路的長度小于N,由于整個圖是連通的,所以在該回路上,一定存在一點與回路之外的點相鄰。那么從該點處把回路斷開,就變回了一條路徑,同時還可以將與之相鄰的點加入路徑。再按照步驟1的方法盡量擴展路徑,則一定有新的節點被加進來。接著回到路徑2.
證明:
可利用鴿巢原理證明。
偽代碼:
設s為哈密頓回路的起始點,t為哈密頓回路中終點s之前的點.ans[]為最終的哈密頓回路。倒置的意思指的是將數組對應的區間中數字的排列順序方向。
1:初始化,令s = 1,t為s的任意一個鄰接點。
2:如果ans[]中元素的個數小于n,則從t開始向外擴展,如果有可擴展點v,放入ans[]的尾部,并且t=v,并繼續擴展,如無法擴展進入步驟3.
3:將當前得到的ans[]倒置,s和t互換,從t開始向外擴展,如果有可擴展點v,放入ans[]尾部,并且t=v,并繼續擴展。如無法擴展進入步驟4.
4:如果當前s和t相鄰,進入步驟5.否則,遍歷ans[],尋找點ans[i],使得ans[i]與t相連并且ans[i +1]與s相連,將從ans[i + 1]到t部分的ans[]倒置,t=ans[i +1],進如步驟5.
5:如果當前ans[]中元素的個數等于n,算法結束,ans[]中保存了哈密頓回路(可看情況是否加入點s)。否則,如果s與t連通,但是ans[]中的元素的個數小于n,則遍歷ans[],尋找點ans[i],使得ans[i]與ans[]外的一點(j)相連,則令s=ans[i - 1],t = j,將ans[]中s到ans[i - 1]部分的ans[]倒置,將ans[]中的ans[i]到t的部分倒置,將點j加入到ans[]的尾部,轉步驟2.
時間復雜度:
如果說每次到步驟5算一輪的話,那么由于每一輪當中至少有一個節點被加入到路徑S -》 T中,所以總的輪數肯定不超過n輪,所以時間復雜度為O(n^2)。空間上由于邊數非常多,所以采用鄰接矩陣來存儲比較適合。
代碼:
const int maxN = 100;
inline void reverse(int arv[maxN + 7], int s, int t){//將數組anv從下標s到t的部分的順序反向
int temp;
while(s 《 t){
temp = arv[s];
arv[s] = arv[t];
arv[t] = temp;
s++;
t--;
}
}
void Hamilton(int ans[maxN + 7], bool map[maxN + 7][maxN + 7], int n){
int s = 1, t;//初始化取s為1號點
int ansi = 2;
int i, j;
int w;
int temp;
bool visit[maxN + 7] = {false};
for(i = 1; i 《= n; i++) if(map[s][i]) break;
t = i;//取任意鄰接與s的點為t
visit[s] = visit[t] = true;
ans[0] = s;
ans[1] = t;
while(true){
while(true){//從t向外擴展
for(i = 1; i 《= n; i++){
if(map[t][i] && !visit[i]){
ans[ansi++] = i;
visit[i] = true;
t = i;
break;
}
}
if(i 》 n) break;
}
w = ansi - 1;//將當前得到的序列倒置,s和t互換,從t繼續擴展,相當于在原來的序列上從s向外擴展
i = 0;
reverse(ans, i, w);
temp = s;
s = t;
t = temp;
while(true){//從新的t繼續向外擴展,相當于在原來的序列上從s向外擴展
for(i = 1; i 《= n; i++){
if(map[t][i] && !visit[i]){
ans[ansi++] = i;
visit[i] = true;
t = i;
break;
}
}
if(i 》 n) break;
}
if(!map[s][t]){//如果s和t不相鄰,進行調整
for(i = 1; i 《 ansi - 2; i++)//取序列中的一點i,使得ans[i]與t相連,并且ans[i+1]與s相連
if(map[ans[i]][t] && map[s][ans[i + 1]])break;
w = ansi - 1;
i++;
t = ans[i];
reverse(ans, i, w);//將從ans[i +1]到t部分的ans[]倒置
}//此時s和t相連
if(ansi == n) return;//如果當前序列包含n個元素,算法結束
for(j = 1; j 《= n; j++){//當前序列中元素的個數小于n,尋找點ans[i],使得ans[i]與ans[]外的一個點相連
if(visit[j]) continue;
for(i = 1; i 《 ansi - 2; i++)if(map[ans[i]][j])break;
if(map[ans[i]][j]) break;
}
s = ans[i - 1];
t = j;//將新找到的點j賦給t
reverse(ans, 0, i - 1);//將ans[]中s到ans[i-1]的部分倒置
reverse(ans, i, ansi - 1);//將ans[]中ans[i]到t的部分倒置
ans[ansi++] = j;//將點j加入到ans[]尾部
visit[j] = true;
}
}
二:N(N》=2)階競賽圖構造哈密頓通路
N階競賽圖:含有N個頂點的有向圖,且每對頂點之間都有一條邊。對于N階競賽圖一定存在哈密頓通路。
數學歸納法證明競賽圖在n 》= 2時必存在哈密頓路:
(1)n = 2時結論顯然成立;
(2)假設n = k時,結論也成立,哈密頓路為V1, V2, V3, 。。。, Vk;
設當n = k+1時,第k + 1個節點為V(k+1),考慮到V(k+1)與Vi(1《=i《=k)的連通情況,可以分為以下兩種情況。
1:Vk與V(k+1)兩點之間的弧為《Vk, V(k+1)》,則可構造哈密頓路徑V1, V2,…, Vk, V(k+1)。
2:Vk與V(k+1)兩點之間的弧為《V(k+1),Vk》,則從后往前尋找第一個出現的Vi(i=k-1,i》=1,--i),滿足Vi與V(k+1)之間的弧為《Vi,V(k+1)》,則構造哈密頓路徑V1, V2, …, Vi, V(k+1), V(i+1), …, V(k)。若沒找到滿足條件的Vi,則說明對于所有的Vi(1《=i《=k)到V(k+1)的弧為《V(k+1),V(i)》,則構造哈密頓路徑V(k+1), V1, V2, …, Vk.證畢。
競賽圖構造哈密頓路時的算法同以上證明過程。
用圖來說明:
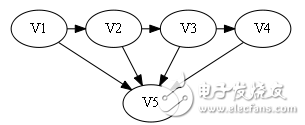
假設此時已經存在路徑V1 -》 V2 -》 V3 -》 V4,這四個點與V5的連通情況有16種,給定由0/1組成的四個數,第i個數為0代表存在弧《V5,Vi》,反之為1,表示存在弧《Vi,V5》
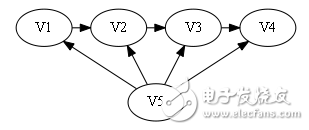
sign[]={0, 0, 0, 0}。
很顯然屬于第二種情況,從后往前尋找不到1,即且不存在弧《Vi, V5》。
則構造哈密頓路:V5 -》 V1 -》 V2 -》 V3 -》 V4.
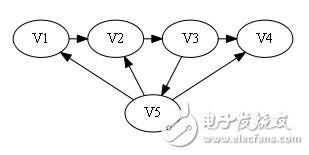
sign[]={0, 0, 0, 1}。
屬于第一種情況,最后一個數字為1,即代表存在弧《Vi, V5》且i=4(最后一個點)
則構造哈密頓路: V1 -》 V2 -》 V3 -》 V4 -》 V5.
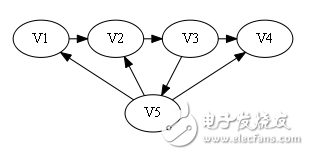
sign[]={0, 0, 1, 0}。
屬于第二種情況,從后往前找到1出現的第一個位置為3.
構造哈密頓路: V1 -》 V2 -》 V3 -》 V5 -》 V4.
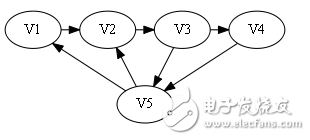
sign[]={0, 0, 1, 1}。
屬于第一種情況,最后一個數字為1,即代表存在弧《Vi, V5》且i=4(最后一個點)
則構造哈密頓路: V1 -》 V2 -》 V3 -》 V4 -》 V5.
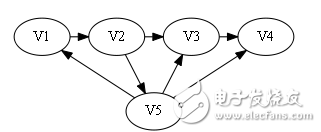
sign[]={0, 1, 0, 0}。
屬于第二種情況,從后往前找到1出現的第一個位置為2.
構造哈密頓路: V1 -》 V2 -》 V5 -》 V3-》 V4.
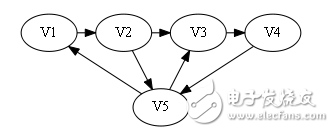
sign[]={0, 1, 0, 1}。
屬于第一種情況,最后一個數字為1,即代表存在弧《Vi, V5》且i=4(最后一個點)
則構造哈密頓路:V1 -》 V2 -》 V3 -》 V4 -》 V5.(就不舉末尾為1的栗子了~~)
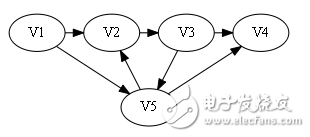
sign[]={1, 0, 1, 0}。
屬于第二種情況,從后往前找到1出現的第一個位置為3.
構造哈密頓路: V1 -》 V2 -》 V3 -》 V5-》 V4.
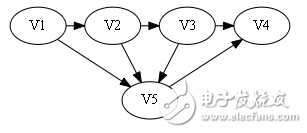
sign[]={1, 1, 1, 0}。
屬于第二種情況,從后往前找到1出現的第一個位置為3.
構造哈密頓路: V1 -》 V2 -》 V3 -》 V5-》 V4.
sign[]={1, 1, 1, 1}。
同樣最后一位為1,代表存在《Vi, V5》且i=4(最后一位)
則構造哈密頓路:V1 -》 V2 -》 V3 -》 V4 -》 V5.以上是當N=4時(N+1=5),用圖來闡述算法的過程。
注意從后往前找不是找這個點編號之前的點,即不是按照編號來的,而是按照當前哈密頓序列從后往前找的。舉個栗子:
4
2 1
1 3
3 2
4 1
4 2
4 3
第一步ans={1}
第二步ans={2,1}
第三步sign={0, 1}(map[3][2] = 0,map[3][1] = 1,當前序列為2,1) ,而不是{1, 0}(1,2),因為存在弧《V1, V3》和《V3, V2》。這里需要注意下。
代碼:
#include 《iostream》
#include 《cmath》
#include 《cstdio》
#include 《cstring》
#include 《cstdlib》
#include 《algorithm》
#include 《queue》
#include 《stack》
#include 《vector》
using namespace std;
typedef long long LL;
const int maxN = 200;
//The arv[] length is len, insert key befor arv[index]
inline void Insert(int arv[], int &len, int index, int key){
if(index 》 len) index = len;
len++;
for(int i = len - 1; i 》= 0; --i){
if(i != index && i)arv[i] = arv[i - 1];
else{arv[i] = key; return;}
}
}
void Hamilton(int ans[maxN + 7], int map[maxN + 7][maxN + 7], int n){
int ansi = 1;
ans[ansi++] = 1;
for(int i = 2; i 《= n; i++){//第一種情況,直接把當前點添加到序列末尾
if(map[i][ans[ansi - 1]] == 1)
ans[ansi++] = i;
else{
int flag = 0;
for(int j = ansi - 2; j 》 0; --j){//在當前序列中,從后往前找到第一個滿足條件的點j,使得存在《Vj,Vi》且《Vi, Vj+1》。
if(map[i][ans[j]] == 1){//找到后把該點插入到序列的第j + 1個點前。
flag = 1;
Insert(ans, ansi, j + 1, i);
break;
}
}
if(!flag)Insert(ans, ansi, 1, i);//否則說明所有點都鄰接自點i,則把該點直接插入到序列首端。
}
}
}
int main()
{
//freopen(“input.txt”, “r”, stdin);
int t;
scanf(“%d”, &t);
while(t--){
int N;
scanf(“%d”, &N);
int M = N * (N - 1) / 2;
int map[maxN + 7][maxN + 7] = {0};
for(int i = 0; i 《 M; i++){
int u, v;
scanf(“%d%d”, &u, &v);
//map[i][j]為1說明j 《 i,且存在弧《Vi, Vj》,因為插入時只考慮該點之前的所有點的位置,與之后的點沒有關系。所以只注重該點與其之前的點的連通情況。
if(u 《 v)map[v][u] = 1;
}
int ans[maxN + 7] = {0};
Hamilton(ans, map, N);
for(int i = 1; i 《= N; i++)
printf(i == 1 ? “%d”:“ %d”, ans[i]);
printf(“ ”);
}
return 0;
}
代碼2:void Hamilton(int ans[maxN + 7], int map[maxN + 7][maxN + 7], int n){
int nxt[maxN + 7];
memset(nxt, -1, sizeof(nxt));
int head = 1;
for(int i = 2; i 《= n; i++){
if(map[i][head]){
nxt[i] = head;
head = i;
}else{
int pre = head, pos = nxt[head];
while(pos != -1 && !map[i][pos]){
pre = pos;
pos = nxt[pre];
}
nxt[pre] = i;
nxt[i] = pos;
}
}
int cnt = 0;
for(int i = head; i != -1; i = nxt[i])
ans[++cnt] = i;
}
代碼三:
void Hamitton(bool reach[N + 7][N + 7], int n)
{
vector 《int》 ans;
ans.push_back(1);
for(int i=2;i 《= n;i++)
{
bool cont = false;
for(int j=0;j《(int)ans.size()-1;j++)
if(reach[ ans[j] ][i] && reach[i][ ans[j+1] ])
{
ans.insert(ans.begin()+j+1,i);
cont = true;
break;
}
if(cont)
continue;
if(reach[ ans.back() ][i])
ans.push_back(i);
else
ans.insert(ans.begin(),i);
}
for(int i=0;i《n;i++)
printf(“%d%c”,ans[i],i==n-1?‘ ’:‘ ’);
}
-
算法
+關注
關注
23文章
4600瀏覽量
92646 -
哈密頓圖
+關注
關注
0文章
3瀏覽量
1276
發布評論請先 登錄
相關推薦

DNA編碼的學習
LaSrAlO4中Cu2+的自旋哈密頓參量的理論分析
ZigBee與哈密瓜不得不說的故事
求解LDPC碼回路的算法
永磁同步直線電機位置控制
模擬量子計算的未來前景將一片光明
模擬量子計算有著優異的表現,未來將具有廣泛的應用前景
模擬量子計算的實力前景不可限量
解決人工智能“智障”新思路——哈密頓函數
基于量子軟件的量子絕熱近似算法求解
基于高光譜的不同成熟期哈密瓜堅實度研究





 哈密頓回路算法
哈密頓回路算法










評論