由于定點的四則運算比較簡單,如加減法只要注意符號擴展,小數點對齊等問題即可。在本文中,運用在前一節中描述的自定義浮點格式FPGA中數的表示方法(下),完成浮點四則運算的實現過程
1.自定義浮點格式加(減)法運算
基于FPGA 實現的浮點加法運算包括了一系列對尾數和指數部分的操作:移位、交換、格式化、舍入和格式化等。如下圖所示,自定義浮點流水加法器實現結構主要分為兩部分:基本加法器部分和格式化操作部分。
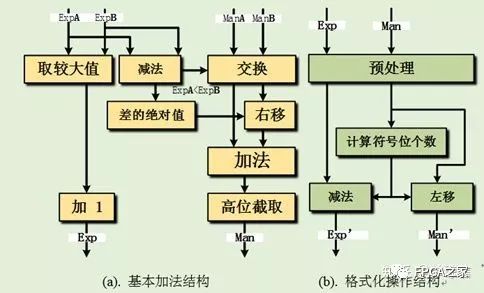
在圖(a)中的基本加法器,首先比較兩個操作數的指數部分,較大的指數加上1之后,寄存輸出(保證流水輸出)作為加法和的指數部分;另一方面根據指數部分的比較結果,交換尾數的位置,即需要對較小的尾數進行右移對齊;之后尾數部分相加,得到的結果高位截取后輸出作為加法和的尾數部分。由于操作數A 和B 的尾數部分首先需要符號位拓展之后進行才進行下一步操作,而最后的和是直接高位截取輸出的,故導致加法結果比實際值小一倍,這就是前面指數需要加上1輸出的原因。對于(b)中的格式化操作,首先對來自基本加法器的尾數和指數進行預處理,然后計算尾數部分的符號位個數。最后根據計算得到的符號位個數,左移尾數后輸出尾數部分,而指數則減去符號位數作為指數部分輸出。
如果是一次而輸入加法則以這樣的結構即可,但如果涉及多次加法,以流水形式完成,則在結構上可以作更好的優化。如下是四輸入和八輸入加法器的結構:
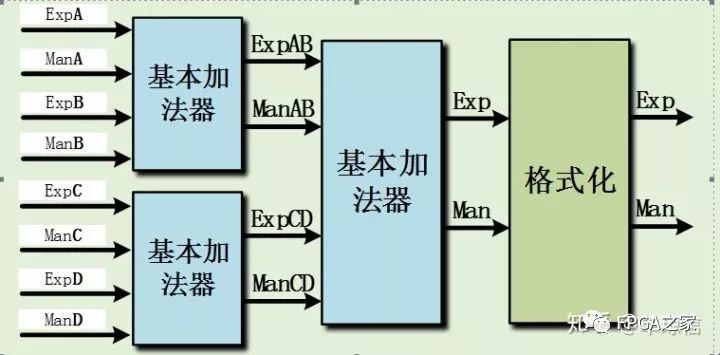
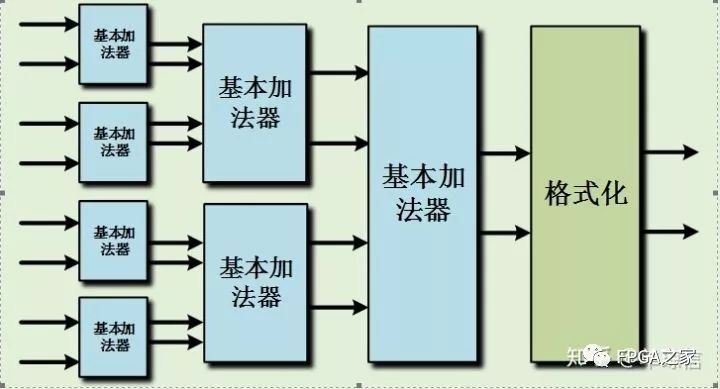
如上所示的情況,可知,這樣的方法可以減少格式化操作,而格式化操作在整個運算過程中消耗相對比較多的資源,因此這樣的實現結構可以有效的減少硬件資源的消耗。
3. 乘加運算
浮點乘法運算較為簡單,對應的尾數部分進行相乘,指數部分進行相加。尾數相乘部分采用XILINX 乘法器IP即可。需要注意的是,乘法結果輸出的位寬指定,在乘法器IP中,按一般流程下來,乘完之后的結果是保留兩位符號位(假設乘數都是一個符號的情況),即多出一個符號位,按小數乘法分析的話,值的情況是比實際結果小一倍,在截位輸出的時候需要做一定的取舍(是從最高位開始截位輸出,還是次高位開始截位輸出;如果從最高位截位輸出,則結果比實際值小一倍,如果從次高位截位輸出只有一種情況會溢出,即兩個乘數都為-1的情況,這種情況如果從次高位截位輸出則會錯誤,其余情況都是正確的)。
這里需要進一步討論的是乘加操作,數字信號處理中常常會遇到操作,如FIR濾波器。按本文的設計思路乘加運算也可以節省一次格式化運算,設計方法如下:
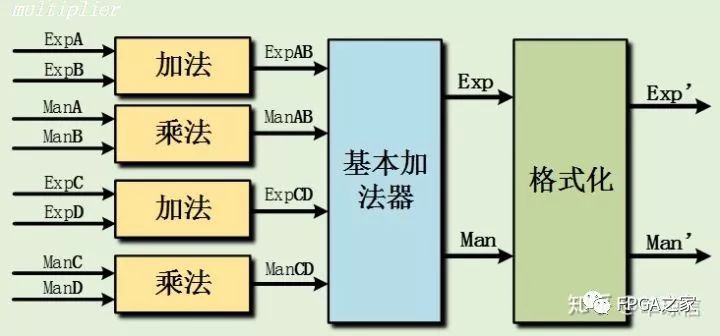
這樣即可省去乘法器中的格式化過程,將乘法的中間結果直接輸入給加法器,最后再進行格式化輸出。
4. 自定義浮點除法器詳細設計
現有的除法硬件實現算法主要可以分為三類:查表法、數字迭代法和函數迭代法。基于查找表的實現方法實現結構簡單,只需進行簡單的查表操作即可,但是其精度多一位,則查找表大小就要增加一倍,顯然不適合實現高精度除法器;數字迭代法中應用最廣的是SRT算法,這類算法基于減法運算,商的精度隨減法迭代次數而線性增長,故為了得到高精度,資源消耗也是相當嚴重。函數迭代算法中最典型的兩種算法是Newton Raphson和Goldschimidt算法,這兩種算法是采用乘法運算來實現對商的精度的逼近,商的精度隨著迭代次數而呈指數增長,適用于高精度的除法運算。
本質上Goldschimidt和Newton Raphson兩種算法的原理是一致的,Goldschimidt算法的實質就是對牛頓迭代算法的迭代操作進行重新排列,使得Goldschimidt算法中的乘法操作可以并行進行處理,故在利用硬件實現除法時,Goldschimidt算法較Newton Raphson在速度上更具優勢。以下詳細分析一下Goldschmidt算法的原理
函數g(y)在p點的泰勒展開公式如下:
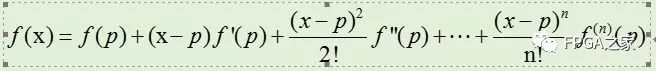
對于除法來說,希望得到如下的等式關系:
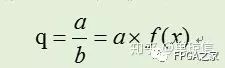
即可以得到倒數函數的展開公式,然而,倒數函數無法作泰勒展開,故采用麥克勞林展開公式,采用的函數表達如下:
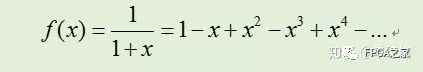
令 f(x)=1/b,則有x=b-1,由0.5≤b<1,得abs(x)≤0.5 ,故:
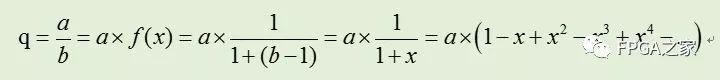
上述公式因式分解后可得如下公式:
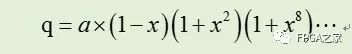
q值可以實現如下迭代過程,其近似的商可以表示如下:
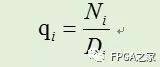
其中Ni和Di分別是算法執行i步后得到的分子和分母。當Di趨近1時,Ni就趨近于q了。迭代開始時,令N0=a,D0=b。第一次迭代,時,N1=R0*N0,其中R0= 1-x = 2-b。可得到如下:
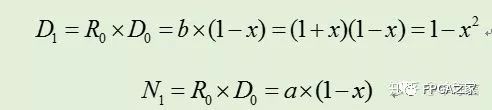
類似地,下次迭代令R1= 2-D1= 1+y^2,則可以得到:
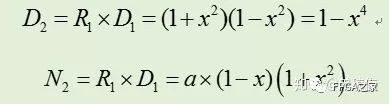
故可以得到Goldschmidt算法的迭代過程,總結如下:
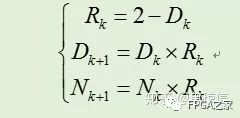
故通過對初始種子進行多次迭代而不斷逼近目標精度。
現有的Glodschimidt算法都是基于標準的IEEE 754雙精度格式,其算法過程可以描述如下圖所示:
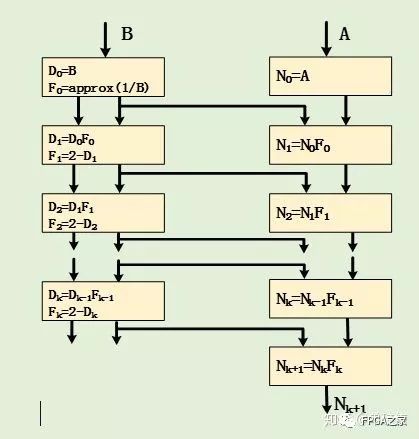
上圖中的approx(1/B)步驟需要得到精度不高的近似的倒數,這里采用直接查找表的形式,這種形式最為簡單,直接查找倒數表得到除數(B)的倒數近似值,然后在使用該值進行上圖所示的函數迭代來得到更高精度的除數倒數逼近值。直接查找表得到的近似值的精度取決于查表的索引長度及其表項長度。故要使初始值的精度增加1位,則查找表的空間就需要翻一倍。對于現階段的FPGA,其存儲資源已經非常多,故在FPGA實現直接查找表,其資源消耗是相對很小的。
IEEE-754標準的浮點數尾數的值范圍為[1,2),在不考慮符號位的情況下,尾數D形如1.d1d2d3…dn。則其倒數范圍(0.5,1]。而自定義的浮點的尾數格式為 .1d1d2d3…dn, 即表示的值的范圍[0.5,1),則其倒數范圍為(1,2]。這樣的區別導致在整個大框架下具體的實現內容情況發生變化。需要對整個算法的每一步驟做好設計。
誠如上述,自定義格式的浮點中,得到的倒數范圍為(1,2],而我們自定義的浮點格式表示的范圍為[0.5,1),故我們須將(1,2]改成(0.5,1] * 2,其中的(0.5,1]由尾數表示,而2則由指數表示。故查找表中的表項表示的值是實際倒數值的1/2。現假設階段后的除數輸入表示為0.1d1d2d3…dn,則輸出的除數倒數值可表示為21 * 0.1b1b2b3…bm,則查表所需的查找表大小為:
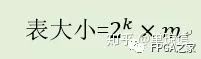
而在FPGA中,采用塊RAM進行實現,每個塊RAM大小36k,而本實現中,初始精度的設計需要達到14位左右,這樣,則輸出位寬m表示為13至16都消耗同等資源,而后邊的算法迭代中,設計的乘法器位寬當為有符號數16x52消耗的DSP48乘法模塊的資源為3,是最為折中的方法,故采用m為15,直接查找表中的每一項直接表示為0.1b1b2b3…bm,這樣表的輸出為16位,正好與后邊的乘法器位寬對應上。
4.1 查找表設計
直接查找表方法中,最常用的是常數分段逼近方法,該算法的核心是確定截斷輸入數0.1d1d2d3…dn0和后一位截斷輸入數0.1d1d2d3…dn1,的中點數值,然后計算該值的倒數,最后加上2^(-(m+2)),并對得到的結果進行舍入到0.1b1b2b3…bm,故查找表中的每一項可以表示為:
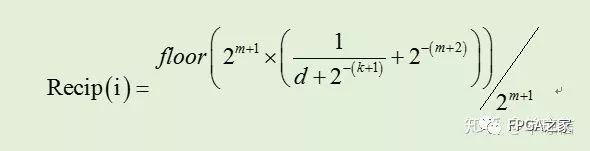
其中0.1d1d2d3…dn。對于輸出位寬m=k+g,能得到的設計精度如下表格:
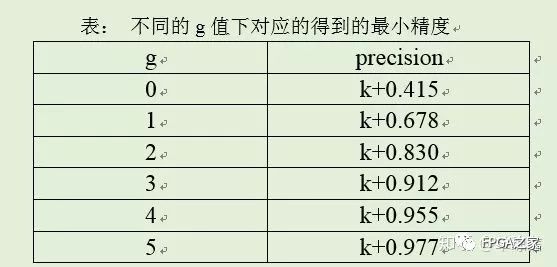
假設確定k=13,m=16,故得到的最小精度為13.912。
4.2 迭代過程
對應的函數迭代過程也發生相應地改變,這里設計時應該考慮每一步驟中的指數變化情況。相應的設計過程如下圖所示:
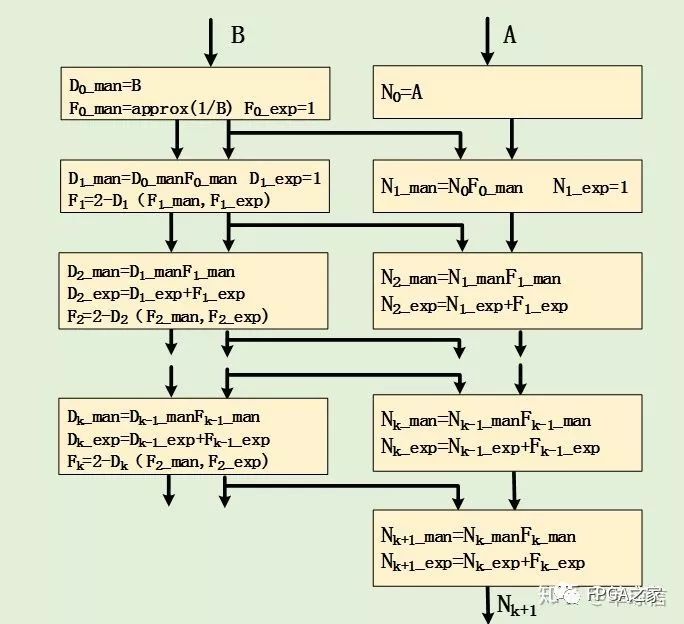
另外在實現多分子單分母,形如(A+C)/B,為了更省時間和空間資源可以采取如下圖所示的實現策略:
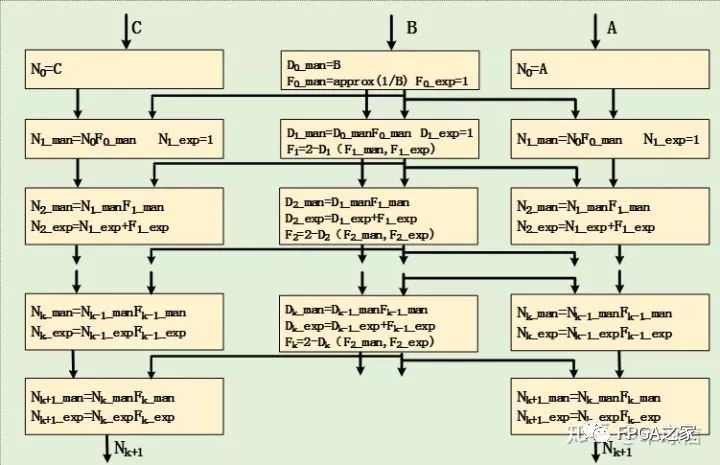
整個算法的流水過程如下:
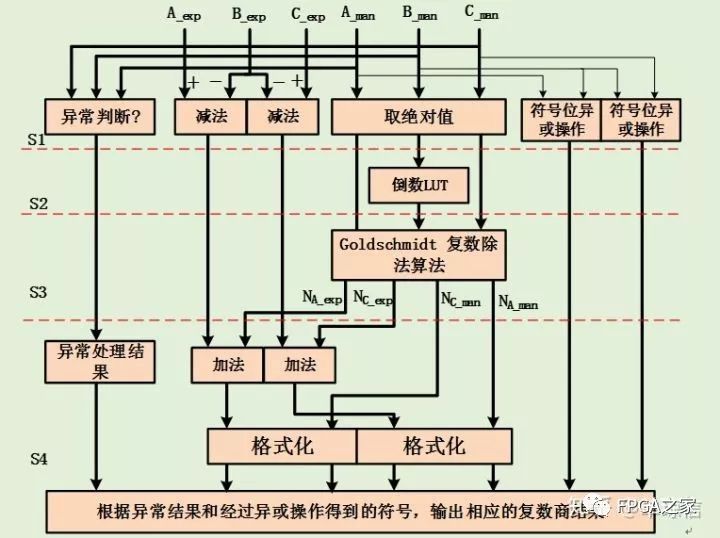
至此,完成自定義浮點格式的四則運算。
-
FPGA
+關注
關注
1626文章
21665瀏覽量
601805 -
運算
+關注
關注
0文章
130瀏覽量
25777
原文標題:FPGA中的浮點四則運算
文章出處:【微信號:Hack電子,微信公眾號:Hack電子】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
霧盈FPGA筆記之(二十五)六位數四則運算計算器(1)整體結構及設計思路
霧盈FPGA筆記之(三十)六位四則運算計算器(6)小算法實現BCD轉二進制
霧盈FPGA筆記之(三十二)六位四則運算計算器(8)算法實現加減乘除
利用simulink設計四則運算仿真模型
如何去實現基于單片機的四則運算計算器設計
使用51單片機設計一個四則運算帶括號的計算器設計報告免費下載
使用51單片機實現簡易四則運算計算器的資料和程序免費下載
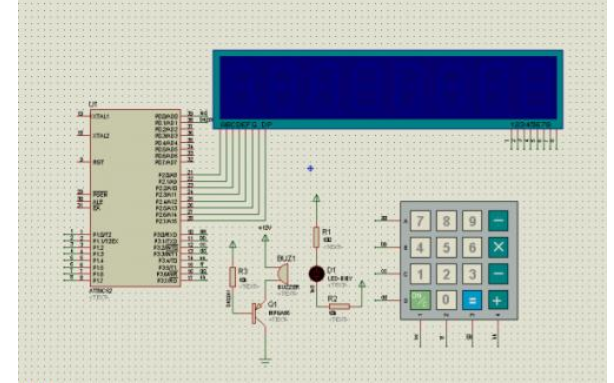
三菱FX系列PLC浮點數運算指令說明
基于單片機四則運算計算器設計+proteus仿真





 FPGA中浮點四則運算的實現過程
FPGA中浮點四則運算的實現過程










評論