量子計算機能夠利用疊加、糾纏和干涉等量子特性,從數據中歸納出知識點并獲得洞察。這些量子機器學習(QML)技術最終將在量子加速的超級計算機上運行,這種超級計算機結合了 CPU、GPU 和 QPU 的處理能力,能夠解決一些世界上最復雜的難題。
許多 QML 算法都假定經典數據可以通過使用所謂的量子隨機存取存儲器(QRAM)進行疊加來實現高效加載,由此提供理論上的加速。由于缺乏實現 QRAM 的有效方法,早期的量子計算機將很有可能只擅長計算,而非數據密集型任務。
實際上,在近期和中期的硬件端上有效運行的 QML 算法必須側重于計算密集型啟發式方法,以便于在沒有 QRAM 的情況下分析數據。
本文將重點介紹愛丁堡大學信息學院量子軟件實驗室副教授 Petros Wallden 博士及其團隊的最新研究成果。Petros 是量子信息學領域的專家,研究范圍涵蓋量子算法、量子密碼學、量子信息學基礎等方面。
Petros 的團隊使用 NVIDIA CUDA-Q(其前身為 CUDA Quantum)平臺開發和加速新 QML 方法的模擬,顯著減少了研究大型數據集所需的量子比特數。
麻省理工學院(MIT)物理學家 Aram Harrow 的研究利用了核心集的概念,為 QML 應用提供了一種新穎的方法,無需 QRAM 就能為其構建現實可行的預言機(oracle)。Petros 的團隊對這一研究進行了擴展。
什么是核心集?
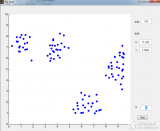
核心集(coreset)是通過提取完整數據集并將其優化映射到較小的加權數據集而形成的(圖 1)。然后,就可以對核心集進行分析,在無需直接處理完整數據集的情況下,近似表示完整數據集的特征。
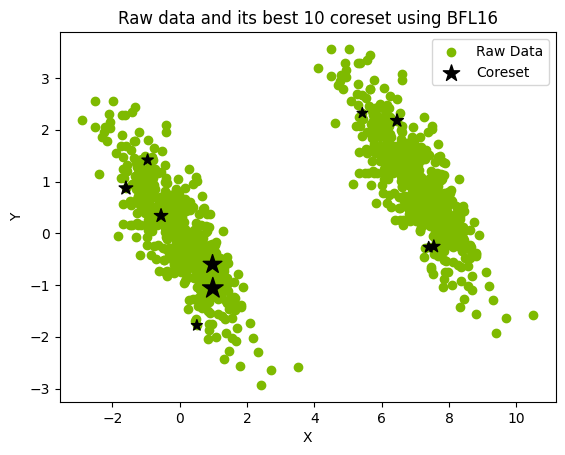
圖 1.用大小為 10 的核心集表示 1000 個點的數據集
核心集是在聚類應用之前采用對數據進行預處理的經典降維方法所產生的結果。通過采用核心集,數據密集型 QML 任務就可以用數量級較少的量子比特來近似表示,并使其成為更加接近實際的近期量子計算應用。
標準的經典核心集構建技術通常先從數據集和目標誤差開始,然后確定核心集的最佳大小,以滿足誤差要求。由于實驗限制,Petros 的團隊根據可用量子比特的數量來選擇核心集的大小,然后在量子計算后評估了這一選擇產生的誤差。
使用核心集進行聚類的量子方法
在將輸入數據縮小到可控大小的核心集后,Petros 的團隊得以探索三種量子聚類算法。
聚類(Clustering)是一種無監督學習方法,該技術描述了一系列以有意義的方式對相似數據點進行分組的方法。這些分組或集群可用于在現實世界的應用中作出明智的決策,例如確定腫瘤是惡性還是良性。
Petros 的團隊使用 CUDA-Q 實現了以下聚類技術:
分裂聚類
在該方法中,核心集數據點從一個集群開始,依次進行雙分區,直到每個數據點都在自己的集群中。該方法可以在第 K 次迭代時停止進程,以便查看數據是如何被劃分到 K 個集群中(圖 2)。
三均值聚類
根據每個數據點與 K 個不斷演化的質量中心(質心)的關系,將數據點劃分到 K 個集群(本例中為 3 個)。當三個集群會聚并且不再隨新的迭代而變化時,過程結束。
高斯混合模型(GMM)聚類
潛在核心點位置的分布被表示為 K 個高斯分布的混合。根據每個核心點最有可能來自哪個高斯分布,將數據分類到 K 個集。
每種聚類技術都會輸出一組核心集,以及原始數據集中的每個點到這些核心集之一的映射。其結果是初始大型數據集的近似聚類和降維。
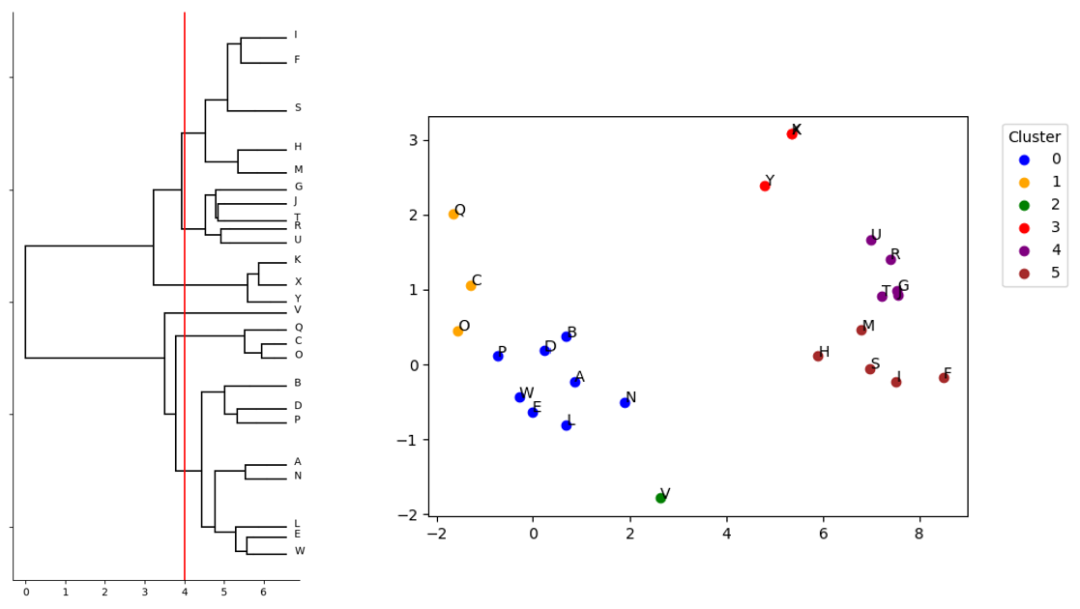
圖 2.N=25 核心集 QML 分裂聚類模擬結果
通過使用變分量子算法(VQA)框架,每種技術都能以使用 QPU 的方式表達。Petros 和其團隊通過推導出一個加權量子比特哈密頓量(受最大切割問題的啟發),為上述每種聚類方法各自的成本函數進行了編碼,從而實現了這一目標。有了這樣一個哈密頓量,VQA 迭代過程就能反復調用真實或模擬的 QPU,從而高效計算每個聚類例程所需的成本最小化。
使用 CUDA-Q 克服可擴展性挑戰
為了探究這些 QML 聚類方法的有效性,就需要對每種算法的性能表現進行模擬。
NVIDIA CUDA-Q 模擬套件可對每種聚類方法進行全面模擬,可處理的最大問題規模為 25 個量子比特。CUDA-Q 通過實現對 GPU 硬件的便捷訪問,加快了這些模擬的速度。其還提供開箱即用的原語,例如用于將基于哈密頓量的優化過程參數化的硬件高效 ansatz 內核,以及可輕松適應聚類算法成本函數的自旋哈密頓量等。
事實上,只有通過 CUDA-Q 提供的 GPU 加速,才能實現 Petros 團隊在其論文《在小型量子計算機上的大數據應用》中提出的模擬規模。
最初的實驗只在 CPU 硬件上模擬了 10 個量子比特,但由于內存限制,無法進行 25 個量子比特規模的實驗。通過 CUDA-Q,最初的 10 個量子比特的模擬代碼實現了即時兼容性,因此當 Petros 的團隊需要將 CPU 硬件換成 NVIDIA DGX H100 GPU 系統時,無需修改即可運行。
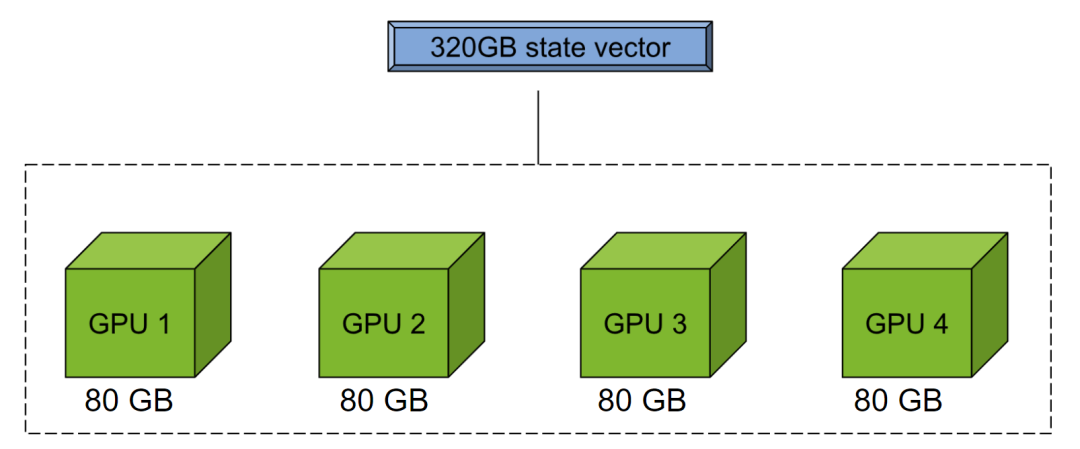
圖 3.CUDA-Q mgpu 后端通過池化多個 GPU 的內存執行大型狀態向量模擬
這種代碼可擴展性是一個巨大的優勢。由于可以使用 NVIDIA mgpu 后端池化多個 GPU 的內存(圖 3),Petros 和其團隊后來在同樣無需大幅修改原始模擬代碼的情況下,通過改變后端目標進一步擴大了模擬規模。
這項研究的主要開發者 Boniface Yogendran 表示:“有了 CUDA-Q,我們就不必擔心量子比特可擴展性方面的限制,從研究開始的第一天起就已經為實現高性能計算做足了準備。”
由于 CUDA-Q 本身也支持 QPU,Yogendran 的代碼可以將這項工作擴展到模擬以外,為所有主要 QPU 模態上的部署提供支持。
CUDA-Q 模擬的價值
由于能夠輕松模擬所有三種聚類算法,Petros 與其團隊得以將每種算法與用于尋找全局最優解的蠻力方法(用于尋找全局最優解)和一種名為勞埃德算法(Lloyd’s algorithm)的經典啟發式方法進行比較。結果表明,量子算法在 GMM(K=2)方面表現最佳,而分裂聚類方法則與勞埃德算法不相上下。
基于這項工作的成功,Petros 的團隊計劃繼續與 NVIDIA 合作,利用 CUDA-Q 繼續開發和擴展新的量子加速超級計算應用。
探索 CUDA-Q
CUDA-Q 使 Petros 和他的團隊能夠便捷地開發出新穎的 QML 實現方法,并利用加速計算對其進行模擬。通過使用 CUDA-Q,可使代碼具有可移植性,以便進一步進行大規模模擬或在物理 QPU 上部署。
了解有關 CUDA-Q 量子的更多信息或馬上開始使用,請參見分裂聚類 Jupyter 筆記本,其中探討了本文中描述的核心集賦能的分裂聚類方法。該教程展示了如何使用 GPU 便捷擴展代碼并運行 34 個量子比特的實例。
-
算法
+關注
關注
23文章
4601瀏覽量
92671 -
機器學習
+關注
關注
66文章
8382瀏覽量
132438 -
量子計算機
+關注
關注
4文章
528瀏覽量
25373
原文標題:通過 CUDA-Q 實現量子聚類算法的資源縮減
文章出處:【微信號:NVIDIA-Enterprise,微信公眾號:NVIDIA英偉達企業解決方案】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
云存儲中大數據優化粒子群聚類算法(基于模糊C均值聚類)
多尺度量子諧振子算法的相空間概率聚類算法
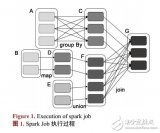
基于Spark的動態聚類算法研究
NVIDIA 通過 CUDA-Q 平臺為全球各地的量子計算中心提供加速





 使用CUDA-Q實現量子聚類算法
使用CUDA-Q實現量子聚類算法










評論