本文較為詳細地介紹半導體的能帶理論。

半導體能帶理論及結構

半導體技術的持續發展得益于半導體理論在固體電子學(隨著固體器件特別是半導體集成電路的空前發展出現的一門新興學科)基礎上的建立與發展，其主要內容可概括為研究半導體中載流子(carrier)按能量狀態的分布、躍遷(能量狀態的改變)和輸運(能量的定向傳遞)。 本文會向大家較為詳細地介紹半導體能帶理論。 對于物質劃分為導體、半導體和絕緣體，主要依據是其電子狀態。 能帶理論：描述固體中電子按能量分布的狀態，從而對導體、半導體和絕緣體從本質上做出科學區分的理論。 能帶理論的基本觀點認為任何固體中所有電子的能級并非按能量均勻分布，而是在某一能量范圍內密集成帶，而與其鄰接的高、低兩個能量范圍卻是電子的能量禁區；或者說固體中所有電子的允許能級皆按其所屬電子性質的不同而密集成不同的能帶，能帶之間由稱為禁帶或能隙的能量禁區隔開。

電子的波粒二象性

電子的波粒二象性是近代電子論從理論和實驗兩方面證明的，其內涵是指電子及其運動既有粒子性特征，也有波動性特征。通常用德布羅意關系來描述電子波粒二象性，其數學表達式如下: P=hk，E=hv 式中，k為波的特征參數波矢k，v為頻率，P，E分別對應動量和能量，h為普朗克常數。 2.自由空間中的電子和周期勢場中的電子 根據經典力學中運動粒子能量與動量的關系和上述德布羅意關系，可將自由空間中電子能量與動量的關系表示為能量與波數(波矢)的關系: E(k)=(hk)^2/2m 這是一個拋物線型的以波數k為自變量的連續函數，式中m為電子性質量。 考慮單個電子在一維周期勢場來概括固體中電子的運動環境，據此求解電子波函數的薛定諤方程，建立了能帶理論的基本構架。結果表明，在一維周期勢場中，受周期勢場的擾動，電子的E(k)函數在=±nπ/2a，n=1,2,3…處不連續、如下圖（圖1）所示：

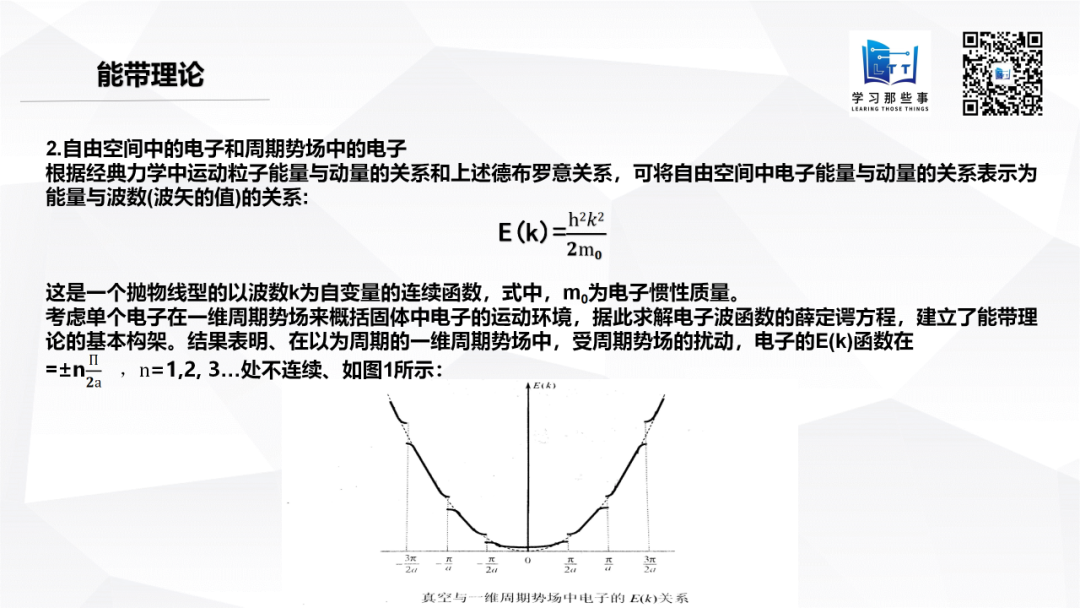
圖1 真空與一維周期勢場中電子的E(k)關系 所謂能帶結構，就是固體中電子的能量與動量之間的關系，即函數E(k)。不涉及電子的動量變化，只是能帶結構的一種簡易表示法，如下圖（圖2）所示：

晶體中出現一個由N條分裂能級構成的s能帶，其N個價電子只能填滿下面一半能級，如(a)所示；絕對零度時，其4N個價電子恰好填滿能量較低的一個能帶(成鍵帶)，能量較高的能帶(反鍵帶)空著，如(b)所示；當原子因為有8個外層電子，其所有分裂能級都會被電子填滿，不會出現空狀態，如(c)所示。 而圖1，可以看做是一個理想一維晶體的E(k)關系。對于實際的三維晶體，其E(k)關系顯然要復雜得多。為了清晰反映某種材料能帶結構的主要特征，通常只在動量空間的兩個特征方向[譬如(100)方向和(111)方向]上畫出E(k)函數曲線。所謂主要特征，就是導帶E(k)函數的極小值和價帶E(k)函數的極大值。重點關注這些極值能量的高低、在k空間出現的位置以及極值處曲線的曲率。 綜上所述：固體中電子狀態之所以符合能帶理論這一特征既與電子的本性(即電子的波粒二象性)有關，也與固體這一電子所處的環境(即原子周期排列形成原子核對電子的周期性勢場)有關。 在圖1中，虛線表示真空中電子的E(k)關系，實線表示周期勢場中電子的E(k)關系，是一個理想一維晶體的E(k)關系。而實際的三維晶體，其E(k)關系會復雜得多。 下圖分別是鍺、硅和砷化鎵三種半導體的能帶結構圖：

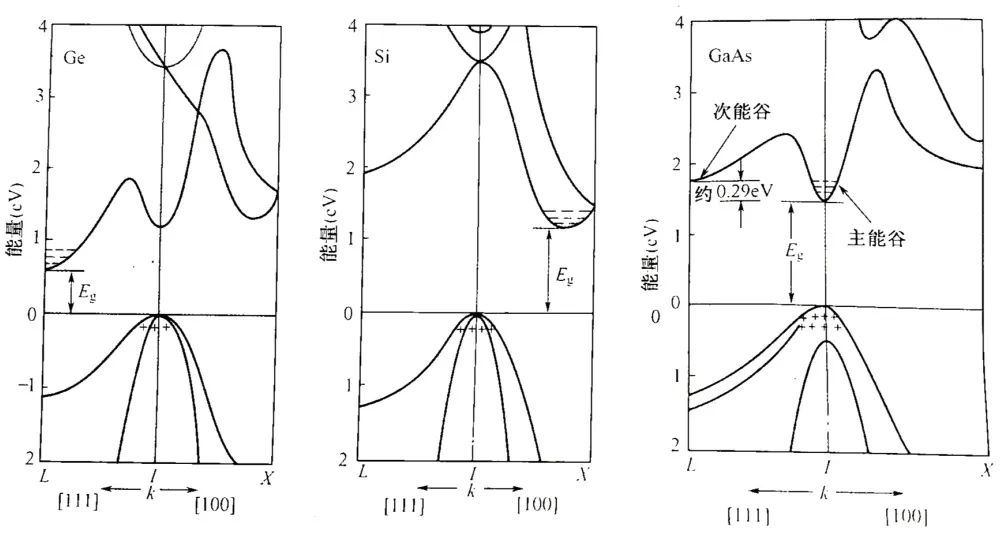
圖中可見，實際材料的導帶E(K)曲線和價帶E(k)曲線都可能不只一條，每條曲線的極值也可能不只一個。決定材料禁帶寬度E(K)的是能量最低的導帶極小值(導帶底)與能量最高的價帶極大值(價帶頂)，而不管這兩個極值是不是對應于同一個k。 上圖呈現了兩種躍遷：直接躍遷和間接躍遷。 間接躍遷：導帶底和價帶頂對應于不同的k，譬如硅和鍺，其電子躍遷前、后必有動量變化，我們稱其為間接躍遷，相應的禁帶叫間接禁帶。 直接躍遷：導帶底和價帶頂對應于同一個k，譬如像砷化鎵那樣，則電子躍遷前、后沒有動量變化，稱為直接躍遷，這種能帶結構的禁帶叫直接禁帶。 能帶結構的另一關注點是它的對稱性。如果一個能帶極值不在k空間的中心，則必有若干等價極值存在于各對稱點。譬如硅的導帶底出現在(100)方向，有6個等價導帶底：鍺的導帶底出現在(111)方向，因此有8個等價的導帶底。 導帶底是導帶電子的最低能量，因此又叫能谷。有些材料的導帶還具有比導帶底略高一點的極小值并兼備其他一些特征，因而具有特殊的實用價值，譬如砷化鎵。為了區別，在這種情況下把導帶底稱為主能谷，較高的極小值稱為次能谷。