仿真預處理的目標是根據分析創建所需的網格。在生成同時解析幾何和物理特征的網格時,我們的目標是提高計算效率。基于仿真預期,我們可以針對流動特征不明顯的特定網格區域進行網格增強。在下圖中,我們在車輛周圍添加了細化區域,因為我們預計這部分會有大量的物理特征,尤其是在尾流區域。這一過程需要運用大量的專業領域知識,并且非常依賴用戶輸入的數據。不過,對流動物理特性極少的區域進行過度細化會增加計算成本和仿真時間,這是不可取的。本文將詳細介紹 Cadence Fidelity Pointwise 中的自動自適應網格細化功能,該功能可管理數值誤差并遵循用戶定義的邊界,同時解析各種應用中的所有流動特征。
1.網格自適應有哪些要求?
網格應滿足以下條件:
符合底層 CAD 幾何圖形
細化符合局部各向異性邊界層
細化較大的和細微的流動特征
在自適應網格細化過程中,我們希望保留邊界層和近壁面的物理特性,使單元大小平滑漸變,確保求解器正常收斂。在自適應網格細化過程中,有必要定義一個自適應傳感器,以便描述需要額外細化的區域。在飛機外部研究中,馬赫數是一個合適的自適應變量,而在渦輪機械應用中,可以將速度大小用作自適應傳感器。
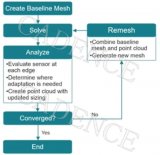
2.使用 Fidelity Pointwise 進行自適應網格細化
在 Fidelity Pointwise 中創建基礎網格,以啟動自適應網格細化。然后,在該網格上運行解。在每個邊緣對傳感器進行評估,如果傳感器在特定位置超過了預定閾值,就會標記為自適應細化。根據點的位置和該區域新的目標單元大小創建點云。然后將點云整合到 Fidelity Pointwise 中的基礎網格中,創建更新后的網格。反復進行這一過程,直到解達到與網格無關的狀態。
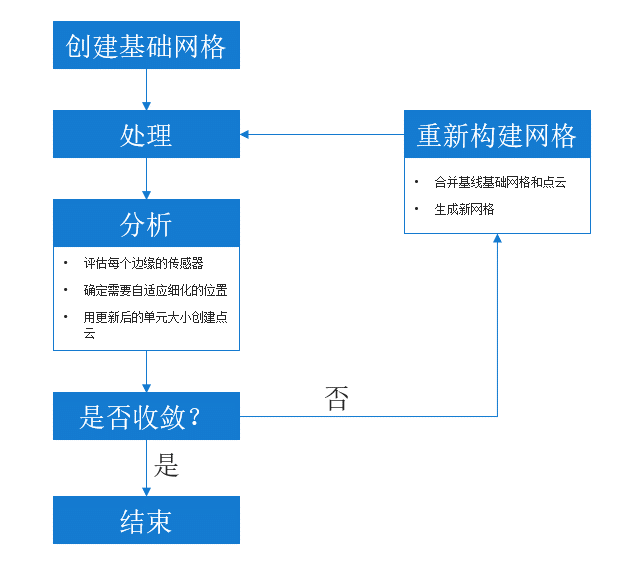
Fidelity Pointwise 中的網格自適應周期
3.應用測試用例
沖擊射流
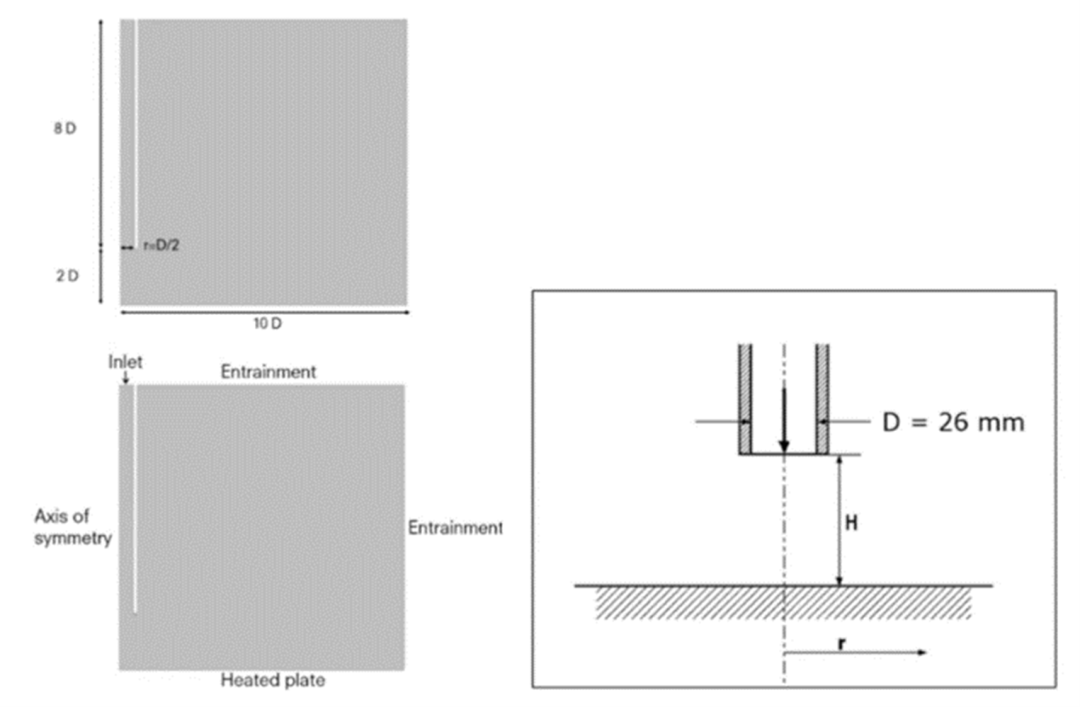
沖擊射流的邊界條件
在上圖中,冷射流降落到熱板上,邊界條件如圖所示。
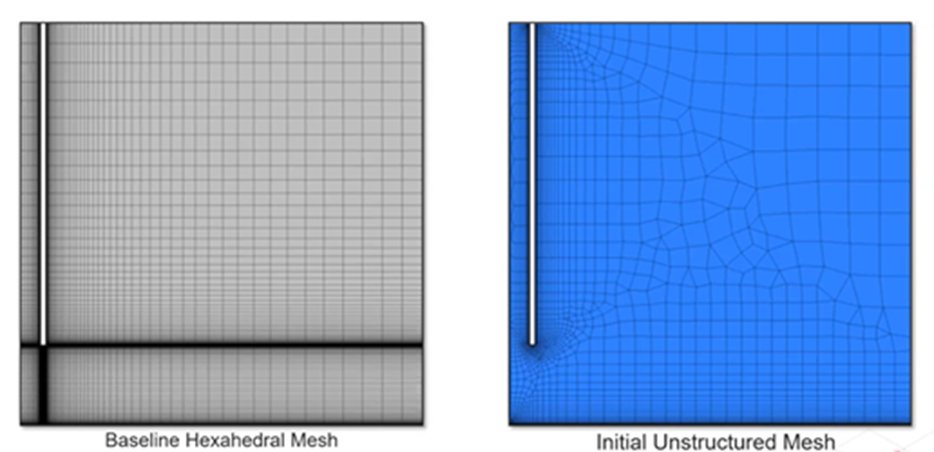
基準網格(左),初始網格(右)
本例的目的是比較完整結構化網格和調整后的網格。在上圖中,左邊的圖片顯示的是基線基礎六面體網格,右邊的圖片顯示的是將根據速度大小進行調整的初始非結構化網格。
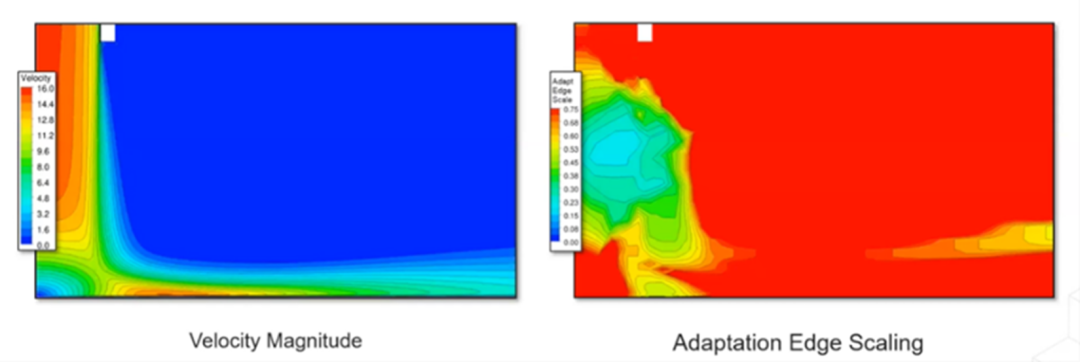
速度大小等值線(左)和自適應邊緣縮放(右)
右圖顯示了當前邊緣通道所需的縮放比例。自適應過程的重點是射流和板之間的區域。根據解創建點云,有 25% 的節點超過了閾值,因此將進行相應的自適應細化。
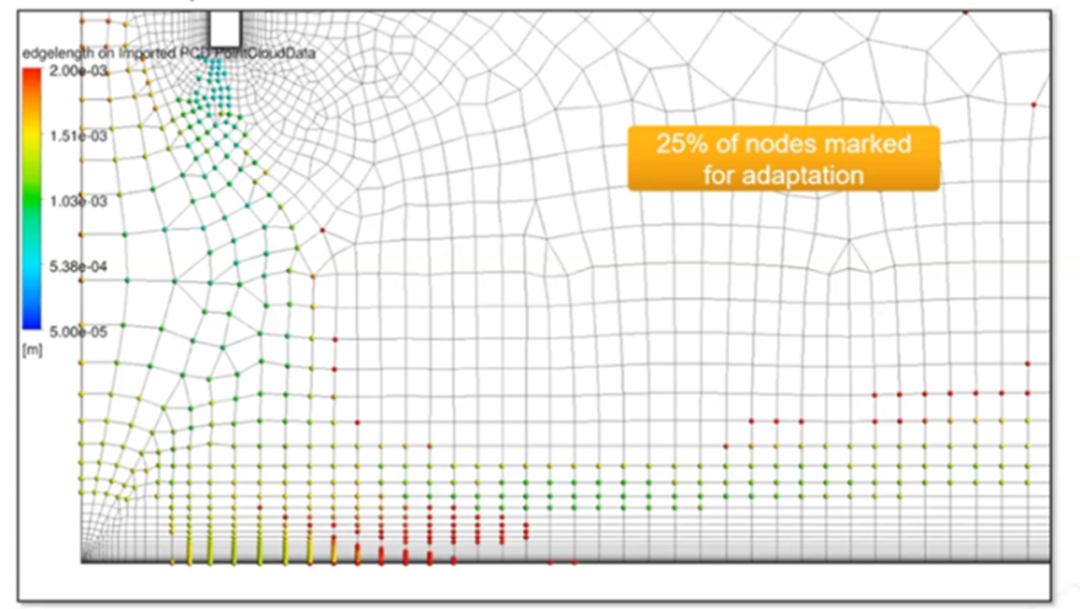
初始點云,有 25% 的節點被標記為自適應節點
在第五個周期中,約有 70% 的節點被標記為自適應節點,而在最后一個周期中,94% 的節點被標記為自適應節點。一旦約 90% 的節點被標記為自適應節點,就可以認為已經收斂。此時可以結束迭代。

第 5 個周期(左)和第 9 個周期(右)中經過自適應細化的網格
檢查網格統計數據后發現,與高度細化的六邊形網格相比,修改后的網格節點和元素更少。放大沖擊區域后,明顯發現初始網格并沒有準確捕捉到數據。然而,網格在經過每個周期后都有所改進,最終更接近實驗數據。
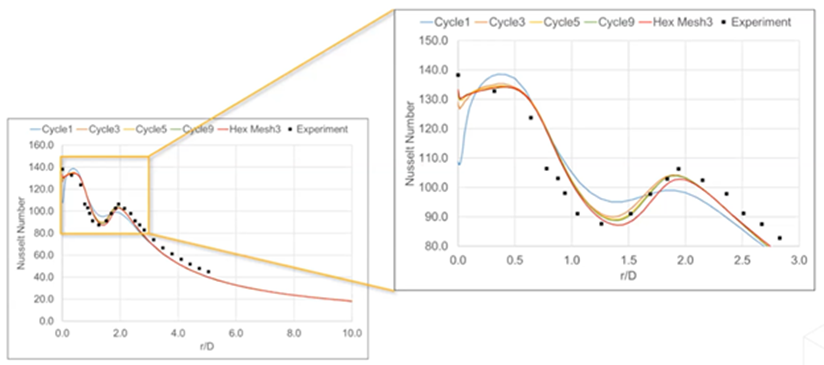
努塞爾數 (Nu) 在經過每個自適應周期后都更接近實驗 Nu 值
軸流式渦輪機葉
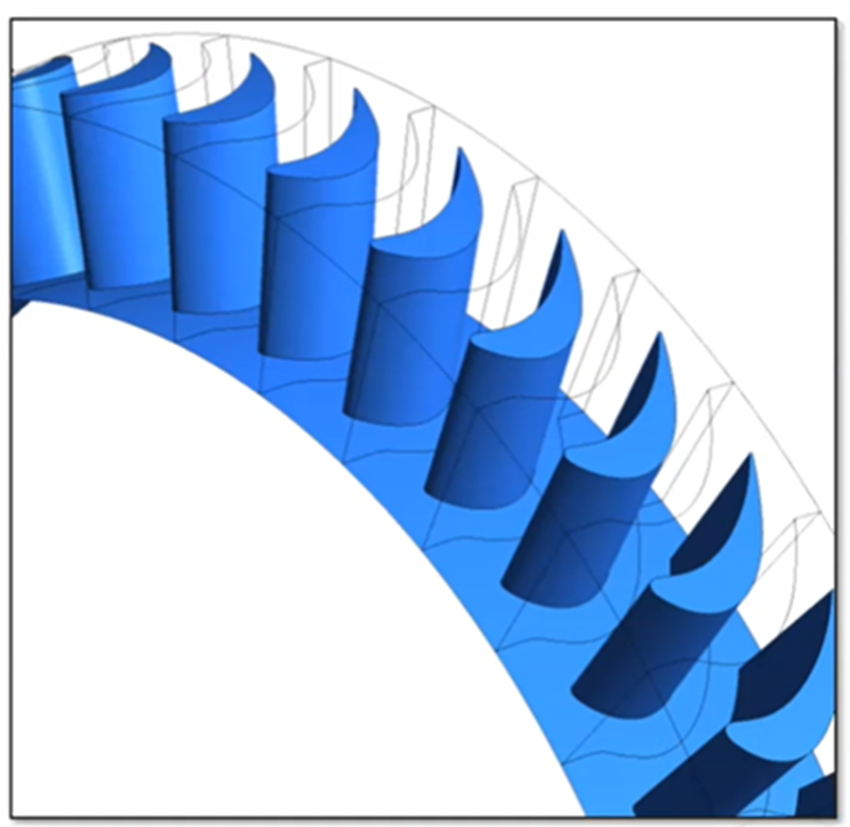
亞琛渦輪機
本測試案例中是一臺亞琛渦輪機,有 41 個葉片,轉速為 3500 RPM。入口和出口流動條件如下表所示:
| Ptotal(入口) | 169,000 Pa |
| Ttotal (入口) | 308 K |
| A(入口) | 49.3° |
| Poutlet | 135,000 Pa(平均) |
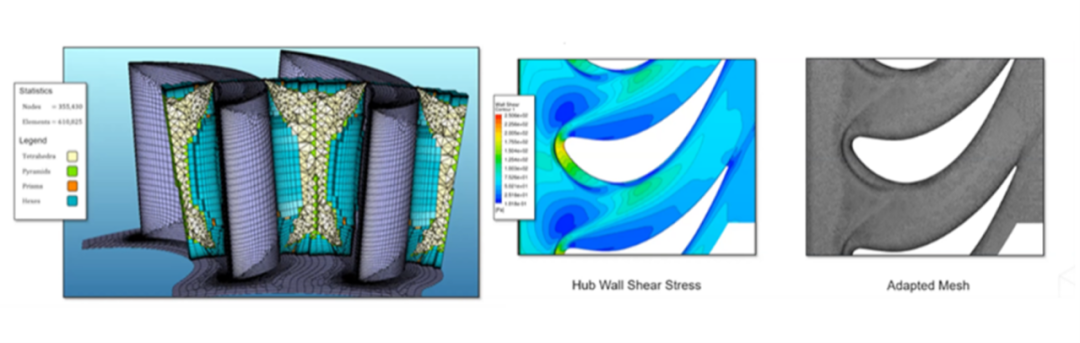
自適應細化的初始網格(左),自適應細化的最終網格 - 葉片區域的切面(右)
這里再次使用速度大小作為自適應變量。在經過自適應細化的網格中,沖擊波清晰可見。此外,經過自適應細化的最終網格準確地反映了二次渦和沖擊波的存在。
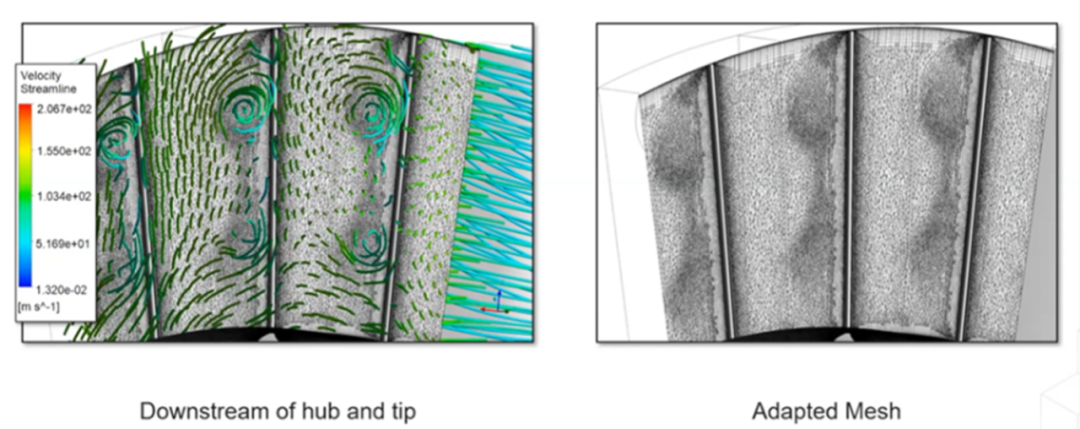
經過自適應細化的網格捕捉到了二次渦流
DrivAer 模型

自適應網格細化也可用于汽車應用,本例中我們使用 DrivAer 模型作為測試案例。將速度大小作為自適應變量。DrivAer 模型的 RANS 仿真使用了 SST 兩方程湍流模型。經過自適應的網格和尾流區域的流線如下所示,顯示出良好的匹配度和對渦流的準確捕捉。
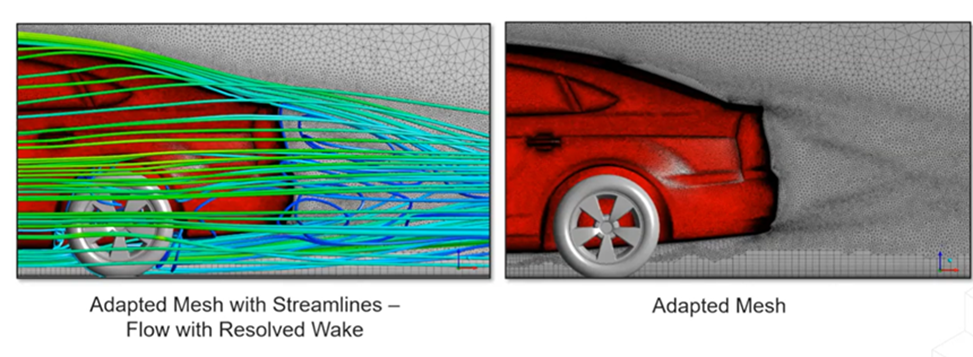
DrivAer 模型經過自適應的網格
外部空氣動力學

DLR F6 模型
該測試案例是第二屆 AIAA 阻力預測研討會上的 DLR F6 模型。馬赫數為 0.75,迎角為 1°。這里的自適應變量是馬赫數。通過自適應網格細化,機翼頂部的沖擊波清晰可見。初始表面壓力和經過自適應細化后的表面壓力如下圖所示。經過每個自適應周期后,沖擊波都會變得更加清晰。

初始網格(左)和經過自適應細化的網格(右)的表面壓力
觀察升力和阻力系數可以發現,每經過一個周期,細化程度都會變得更加精確。這種網格自適應方法可以輕松集成到任何工作流程中。
雖然一開始需要花費一些精力進行設置,但一旦設置妥當,剩下的流程就可以自動完成。在自適應周期中,因為每次都會返回到基線基礎網格,所以拓撲結構將保持一致。
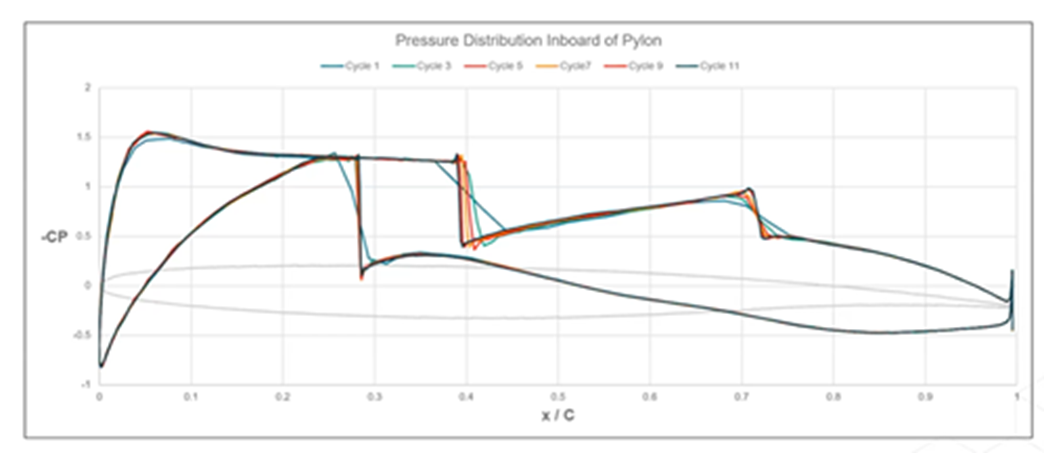
適應周期期間的升力和阻力系數
4.高階網格彎曲
高階網格彎曲是一項新興技術,對于在計算流體力學(CFD)求解器領域中使用有限元方法(FEM)的設計人員來說,這項技術將成為他們的得力助手。與有限體積法和有限差分法等傳統 CFD 方法相比,有限元技術能以較少的元素提高準確度。這要歸功于有限元方法在線性元素的邊、面和內部引入了額外的頂點(新的自由度)。對于與彎曲幾何體相鄰的元素,這些新自由度必須位于幾何體上,從而改變原始線性元素的形狀。當網格中有一組元素向粘性邊界聚類時,這一過程會更加困難。內部元素的邊和面也必須根據邊界元素的曲率進行彎曲,以避免元素反轉。
對 Cadence Fidelity Pointwise 所使用的 WCN 平滑處理進行研究,允許混合階網格求解幾何曲率。在高度彎曲的幾何體附近,元素最高可升階至四次多項式(四次方),而在遠離彎曲幾何體的地方,元素仍然保持線性。網格平滑方法使用代價函數來強制保持所需的元素形狀和每個元素的正雅可比。當元素在幾何體附近彎曲時,粘性網格間距保持不變。研究顯示了復雜 3D 配置的效果。
-
傳感器
+關注
關注
2548文章
50740瀏覽量
752143 -
仿真
+關注
關注
50文章
4048瀏覽量
133431 -
汽車
+關注
關注
13文章
3433瀏覽量
37180
發布評論請先 登錄
相關推薦
EM網格頻率和網格密度問題
【ELT.ZIP】OpenHarmony啃論文俱樂部——即刻征服3D網格壓縮編碼
樹型網格計算環境下的自適應任務調度算法
網格作業自適應遷移模型
基于自適應網格的快速步進法

多重網格格子Boltzmann方法
基于網格與加權信息熵的改進算法
為什么矩形自適應網格是先進技術?
基于線性網格創建高階網格
什么是網格劃分或網格生成?

技術資訊 I 如何在 CFD 設計中利用網格維護幾何形狀并減少運行時間?





 利用自適應網格細化功能自動生成最佳網格
利用自適應網格細化功能自動生成最佳網格











評論