一種非常簡單的壓縮方法是行程長度編碼,這種方法使用數據及數據長度這樣簡單的編碼代替同樣的連續數據,這是無損數據壓縮的一個實例。這種方法經常用于辦公計算機以更好地利用磁盤空間、或者更好地利用計算機網絡中的帶寬。對于電子表格、文本、可執行文件等這樣的符號數據來說,無損是一個非常關鍵的要求,因為除了一些有限的情況,大多數情況下即使是一個數據位的變化都是無法接受的。
對于視頻和音頻數據,只要不損失數據的重要部分一定程度的質量下降是可以接受的。通過利用人類感知系統的局限,能夠大幅度得節約存儲空間并且得到的結果質量與原始數據質量相比并沒有明顯的差別。這些有損數據壓縮方法通常需要在壓縮速度、壓縮數據大小以及質量損失這三者之間進行折衷。
有損圖像壓縮用于數碼相機中,大幅度地提高了存儲能力,同時圖像質量幾乎沒有降低。用于DVD的有損MPEG-2編解碼視頻壓縮也實現了類似的功能。
在有損音頻壓縮中,心理聲學的方法用來去除信號中聽不見或者很難聽見的成分。人類語音的壓縮經常使用更加專業的技術,因此人們有時也將“語音壓縮”或者“語音編碼”作為一個獨立的研究領域與“音頻壓縮”區分開來。不同的音頻和語音壓縮標準都屬于音頻編解碼范疇。例如語音壓縮用于因特網電話,而音頻壓縮被用于CD翻錄并且使用 MP3 播放器解碼。
壓縮,是為了減少存儲空間而把數據轉換成比原始格式更緊湊形式的過程。數據壓縮的概念相當古老,可以追溯到發明了摩爾斯碼的19世紀中期。
摩爾斯碼的發明,是為了使電報員能夠通過電報系統,利用一系列可聽到的脈沖信號傳遞字母信息,從而實現文字消息的傳輸。摩爾斯碼的發明者意識到,某些字母比其他字母使用地更頻繁(例如E比X更常見),因此決定使用短的脈沖信號來表示常用字母,而使用較長的脈沖信號表示非常用字母。這個基本的壓縮方案有效地改善了系統的整體效率,因為它使電報員在更短的時間內傳輸了更多的信息。
雖然現代的壓縮流程比摩爾斯碼要復雜地多,但是它們仍然使用著相同的基本原理,也就是我們這篇文章中將要講述的內容。這些概念對我們如今的計算機世界高效運行至關重要——互聯網上從本地與云端存儲到數據流的一切東西都嚴重依賴壓縮算法,離開了它很可能會變得非常低效。
壓縮管道
下圖展示了壓縮方案的通用流程。原始的輸入數據包含我們需要壓縮或減小尺寸的符號序列。這些符號被壓縮器編碼,輸出結果是編碼過的數據。需要注意的是,雖然通常編碼后的數據要比原始輸入數據小,但是也有例外情況(我們后面會講到)。
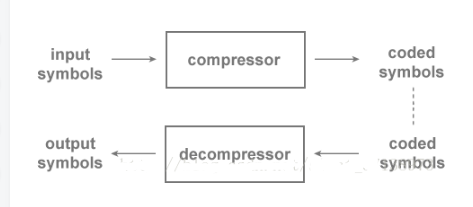
通常在之后的某個時間,編碼后的數據會被輸入到一個解壓縮器,在這里數據被解碼、重建,并以符號序列的形式輸出原始數據。注意,本文我們會交替地使用“序列”和“串”來指一個符號序列集。
如果輸出數據和輸入數據始終完全相同,那么這個壓縮方案被稱為無損的,也稱無損編碼器。否則,它就是一個有損的壓縮方案。
無損壓縮方案通常被用來壓縮文本,可執行程序,或者其他任何需要完全重建數據的地方。
有損壓縮方案在圖像,音頻,視頻,或者其他為了提高壓縮效率而可以接受某些程度信息丟失的場合很有用處。
數據模型
信息的定義是度量一個數據片段復雜度的量。一個數據集擁有越多的信息,它就越難被壓縮。稀有的概念和信息的概念是相關的,因為稀有符號的出現比常見符號的出現提供了更多的信息。
例如,“日本的一次地震”的出現比“月球的一次地震”提供的信息號少,因為月球上的地震很不常見。我們可以預期,大多數壓縮算法在壓縮一個符號時,能夠仔細地考慮它出現的頻率或幾率。
我們把壓縮算法降低信息負載的有效性,稱為它的效率。一個效率更高的壓縮算法相比效率低的壓縮算法,能夠更多地降低特定數據集的大小。
概率模型
設計一個壓縮方案的最重要一步,是為數據創建一個概率模型。這個模型允許我們測量數據的特征,達到有效的適應壓縮算法的目的。為了使它更加清晰一些,讓我們瀏覽一下建模過程的部分環節。
假設我們有一個字母表G,它由數據集中所有可能出現的字符組成。在我們的例子中,G包含4個字符:從A到D。
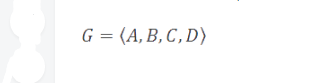
我們還有一個概率統計函數P,它定義了在輸入數據串中,G中每個字符出現的概率。在輸入數據串中,概率高的符號比概率低的符號更有可能出現。

在這個例子中,我們假定符號是獨立同分布的。在源數據串中,一個符號的出現與其他任何符號沒有相關性。
最小編碼率
B是最常見的符號,出現的概率是40%;而C是最不常見的符號,它的出現概率只有10%。我們的目標是設計一個壓縮方案,它對于常見符號使所需存儲空間最小化,同時它支持使用更多的必要空間來存儲不常見符號。這個折衷是壓縮的基本原理,并且已經存在于幾乎所有的壓縮算法中。
有了字母表,我們可以小試身手,來定義一個基本的壓縮方案。如果我們簡單地把一個符號編碼為8比特的ASCII值,那么我們的壓縮效率,即編碼率,將是8比特/符號。假定我們對只包含4個符號的字母表改進這個方案。如果我們為每個符號分配2個比特,我們仍然能夠完全重建編碼過的數據串,而只需要1/4的空間。
ASCII
在計算機中,所有的數據在存儲和運算時都要使用二進制數表示(因為計算機用高電平和低電平分別表示1和0),例如,像a、b、c、d這樣的52個字母(包括大寫)、以及0、1等數字還有一些常用的符號(例如*、#、@等)在計算機中存儲時也要使用二進制數來表示,而具體用哪些二進制數字表示哪個符號,當然每個人都可以約定自己的一套(這就叫編碼),而大家如果要想互相通信而不造成混亂,那么大家就必須使用相同的編碼規則,于是美國有關的標準化組織就出臺了ASCII編碼,統一規定了上述常用符號用哪些二進制數來表示。
它是現今最通用的單字節編碼系統。
這時候,我們已經顯著地提升了編碼率(從8到2比特/符號),但是完全忽視了我們的概率模型。正如前面提到的,我們可以結合模型發明一個策略,通過對常見符號(B和D)使用更少的比特,對不常見符號(A和C)使用更多的比特,以提高編碼效率。
這提出了一個在香農開創性論文中描述的重要觀點——我們可以簡單地基于符號(或事件)的概率,定義它的理論最小存儲空間。我們如下定義一個符號的最小編碼率:
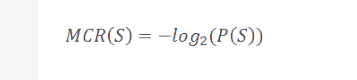
例如,如果一個符號出現的概率是50%,那么它絕對最少需要一個字節來存儲。
熵和冗余
更進一步,如果我們為字母表中的字符計算最小編碼率的加權平均值,我們得到一個被稱作香農熵的值,簡單地稱作模型的熵。熵被定義為給定模型的最小編碼率。它建立在字母表和它的概率模型之上,如下描述。
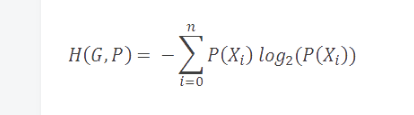
正如你預料的一樣,擁有更多罕見符號的模型,比擁有較少并且常見符號的模型的熵要高。更進一步,熵值更高的模型比熵值低的模型更難壓縮。
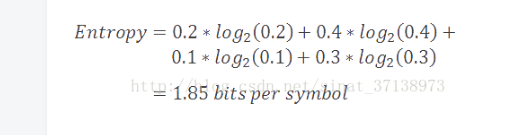
在我們當前的例子中,我們模型的熵值是1.85比特/符號。編碼率(2)和熵值(1.85)的差值被稱作壓縮方案的冗余。
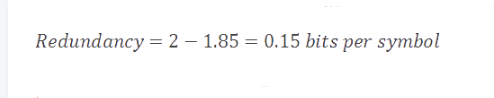
在眾多諸如加密和人工智能等不同的子領域,熵都是一個非常有用的話題。
編碼模型
到目前為止,我們采取了一點點自由措施:自動地給出了我們符號的概率。在現實中,模型通常并不是容易得到的,我們可能通過分析源數據串(如在樣例數據匯總統計符號概率),或者在壓縮過程中自適應地學習,以得到這些概率值。不管是哪種情形,真實數據串的概率值不會完美地與模型匹配,而且我們會與這個差別正比例地損失壓縮效率。基于這個原因,推導出(或恒定地保持)一個盡可能精確的模型是至關重要的。
常見算法
當我們為數據集定義了概率模型之后,我們就能夠適當地利用這個模型設計出一個壓縮方案。雖然開發一個新壓縮算法的過程超出了本文的范圍,但是我們可以利用已經存在的算法。下面我們回顧一些最流行的算法。
下面的每一個算法都是一個順序處理器,這就是說如果要重建已編碼序列的第n個符號,必須先對第0.。(n-1)個符號進行解碼。由于編碼后數據的不定長特性,尋找操作是不可能的——解碼器在不解碼前面的符號的情況下,無法直接跳轉到符號n的正確偏移位置。另外,一些編碼方案依賴于順序處理每個符號時保持的內部歷史狀態。
霍夫曼編碼
這是一個最為廣泛知曉的壓縮方案。它能夠追溯到19世紀50年代,David Huffman在他的論文“一種構建極小多余編碼的方法”中第一次描述了這種方法。霍夫曼編碼通過得到給定字母表的最優前綴碼工作。
一個前綴碼代表一個數值,并使字母表中的每個符號的前綴碼不會成為另一個符號前綴碼的前綴。例如,如果0是我們第一個符號A的前綴碼,那么字母表中的其他符號都不能以0開始。由于前綴碼使比特流解碼變得清晰明確,因此很有用。
字典方法
這種類型的編碼器使用一個字典來保存最近發現的符號。當遇到一個符號時,首先會在字典中查找它,檢查是否已經存儲過了。如果是,那么輸出將只包含字典入口的引用(通常是一個偏移量),而不是整個符號。
使用字典方法的壓縮方案包括LZ77 and LZ78,它們是很多不同的無損壓縮方案的基礎。
在一些情況下,會使用一個滑動窗口來自適應地追蹤最近發現的符號。這種情況下,一個符號只在相對較近發現時才會保存在字典中。否則,符號被剔除(之后再出現可能會重新加入字典)。這個過程防止符號字典變得過大,并利用了一個事實,即序列中的符號會在相對短的窗口內重復出現。
哥倫布指數編碼
假設你有一個由0到255范圍內的整數組成的字母表,并且一個符號的出現概率與它到0的距離有關。這樣,比較小的值是最常見的,而值越大出現的概率越小。
和大多數壓縮方案一樣,哥倫布編碼的效率非常依賴于輸入序列中的特定符號。包含很多大值的序列與包含較少大值的序列相比,壓縮效果更差一些;在某些情況下,經過哥倫布編碼后的序列甚至可能比原始輸入串的尺寸更大。
算數編碼
算數編碼是一個比較新的壓縮算法,在最近(過去的15年里)得到了極大的普及,特別是媒體壓縮方面。算數編碼器是一種高效率,計算密集型,具有時序性的編碼器。
一個常見的算數編碼變種,二進制算數編碼,使用只包含兩個符號(0和1)的字母表。這個變種特別有用處,因為它簡化了編碼器的設計,降低了運行時的計算代價,并且在編碼器和解碼器處理一個字母表和模型時,不需要任何顯式的通訊。
行程長度編碼
到現在為止,我們已經假設源符號是獨立同分布的。我們的概率模型和編碼率與熵的計算方法都依賴于這個事實。但是,如果我們的符號序列不滿足這個要求呢?
假設我們序列中符號的重復度很高,并且一個特定符號的出現有力地表明,它的重復實例即將跟隨出現。這種情況下,我們可以選擇使用另一個稱作行程長度編碼的編碼方案。這種技術在符號重復度很高時表現良好,而在重復度低時表現較差。
行程長度編碼器預測數據串中連續重復符號的長度,并使用這個符號和重復次數來替代它們。
-
數據壓縮
+關注
關注
0文章
31瀏覽量
10131 -
無損壓縮
+關注
關注
0文章
12瀏覽量
8435
發布評論請先 登錄
相關推薦
FPGA實現滑動平均濾波算法和LZW壓縮算法
【TL6748 DSP申請】井下數據壓縮技術
請問有沒有32可用的數據壓縮算法?
GPS定位數據壓縮算法的設計與實現
GPS定位數據壓縮算法的設計與實現
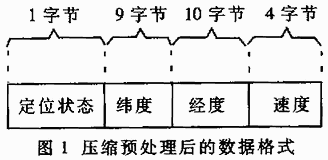




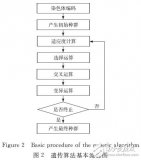
 數據壓縮算法計算步驟及過程
數據壓縮算法計算步驟及過程











評論