補碼就是正數的原碼的相反數的另一種編碼方式。它能把字長內的正數,補足為全是0。
補碼的意義:
現實生活中,我們有加法、減法、乘法和除法,但在計算機中只有一個加法器。換句話說,加法運算在計算機中可以直接完成,減法、乘法和除法運算最終也得轉換為加法才能實現,說到這里,可以有些初學者會想,為什么計算機中不設計一個類似于“加法器”的“減法器”或者“乘法器”的部件,主要原因是在生活中看似一些很簡單的東西要用電路來實現都很復雜、很困難的,再說如果用一個加法器可以實現其它運算,其它的“加法器”、“減法器”或者“乘法器”也就沒有必要了,這樣還能使電路的設計更簡單。好了,現在我簡要地說一下補碼在計算機中的意義,計算機不能直接做減法,必須把相應的減法變成加法,才能進行計算。然而我們發現,一個數減去另外一個數,與一個數加上“另外一個數的補碼”結果是一樣的。這就是補碼對于計算機的意義:將減法運算變成了加法運算。
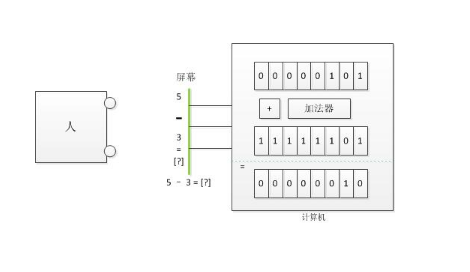
補碼有什么用?
正數的補碼,就是基本身
負數的補碼,就是原碼按位取反加1
符號位,就是最高位,最左面的第一位;其它位,就是剩下的7位
由于運算器進行加法是最快的,因此,使用補碼是為了加快計算
碼”和“數”是兩個東西。
我們平時說出或寫出某“數”,一般都是在十進制下,用10個不同的“碼”(此處的“碼”還和原碼補碼反碼的概念不同)來表示。分別是0~9。超過9,也就是比最大的碼還大的數,采用進位的方式來表示。于是有了“位”的概念。即個位,十位,百位等等。
表達負數的時候由于為了與算術和代數符號當中減號或作差相互兼容,就在該數前面加上減號。
這種對一個數的寫法也可以被名門為一種編碼方式。在這種編碼方式下每個數都有一定的“位數”,即“長度”。在計算機當中規定一定的位數稱作“字長”,比如4位,8位,16位,32位等等。只不過,計算機的物理存儲數據是二進制方式。我們人類目前傳統的還是比較喜歡用10進制方式。并且,我們人類一般不會在書寫數字的時候遇到“字長”的概念。但是在念數字和記錄數據的時候,有一點點東西跟字長相關。比如西方愛把數據分成三位一組三位一組的方式,覺得比較好記憶。比如12‘000讀成十二千,我們中國人愛以“萬”為字長,1’2000,讀作一萬二千。舉這個例子表示字長的概念不是很恰當。因為對人而言這只是一種表達習慣。但是對機器而言,“字長”則是計算的長度單位。設計計算機進行最簡單的加法運算,首先要考慮的就是加法器進行一次加法運算,位數是多長?加法器設計成多少位的加法器?等等。這就是計算機的字長。它和編碼方式一起,構成了計算機進行計算的基礎。
有了字長的概念才好說補碼。
在十進制下也有補碼的概念。插一句,談到補碼一定要先明確字長的長度。
補碼是用來表示負數的一種編碼方式。也是為了在計算機的核心加法器部分的設計避免減法操作,存儲數據的時候避免存儲負號。
舉個例子,假如我們模擬一個字長為4位的十進制計算機。(假設有某種機制,可以在1位上有10種穩定的狀態)
對兩個數進行求和運算:1234 和 -1234
如果用原碼,那么我們需要用一個1位的寄存器來存儲和表示負號。假設就在4位的最左邊的最高位前用1表示負號,0表示正號。
則,原碼表示上面兩個數:
0 1234
1 1234
然后計算機做求和,做加法的過程中。計算機發現,其中有一個數是負數,于是要切換為兩個正數相減的模式來運算。這很不方便。
于是,補碼被想出來了。
-1234和正1234相加不是等于0000嗎?在4位的字長當中的數,和1234相加為0000的,是不是唯一的一個數哪?很明顯8766和1234相加等于1‘0000,后4位是0000。
那么,8766就可以看著是-1234的一種編碼表示方式,被稱作“補碼”。
所以,補碼就是把數1234在一個字長內,補足為1’0000的數的編碼方式。也就是一個正數的相反數,在計算機內的表達方式。
加上符號位,正數0‘1234的相反數的補碼表示就是1’8766。
十進制里,-1234的反碼就是1‘8765
所以,現在回到4位字長的2進制計算機里來看。補碼和反碼的構成方式是一樣的。0’0001的相反數是-1。
補碼表示1‘1111
反碼表示1’1110
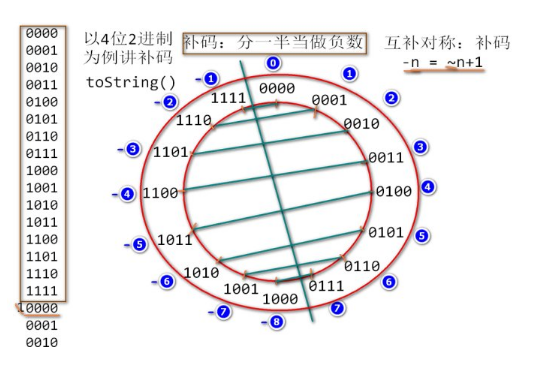
補碼是誰發明的
誰發明的未知,但根據wikipedia上的說法,最初是馮諾依曼引入到計算機的。
很早以前,許多計算機的內部數值編碼是用的反碼,反碼這玩意有缺點: 它的值域內有-0和+0,一個數與它的補數相加為-0,這給運算帶來一些麻煩。
補碼就沒有這些問題,不但只有一個0,而且補碼的加減乘法都可以化簡為加法一種方式。 所以在計算機里補碼對簡化運算器有很大的作用。
補碼的回顧以及補碼發明的思路推演思考
補碼與求補運算的定義
N個二進制位,M=N-1
通過一種編碼映射。100.。.00 - 111.。.11 表示 (-2^M) - (-1) ; 000.。.00 - 011.。.11 表示 (0) - (2^M - 1)
對于編碼A的求補 f(A) = (2^N)- A
原碼轉化成補碼:
對于正數和零,原碼即是補碼
對于負數A,一般理解方法:
先做反碼,然后編碼意義上加1
求補運算的意義:
換言之,若要對一個數A求反,對那個數的補碼A1做一次求補運算f(A1),所求的補碼B1就是原來數A的相反數B的補碼。
這里提供原碼轉化成補碼另外一個理解方法
對于求負數A的補碼
本質上,負數A的相反數B,B是正數,B的原碼B1就是B的補碼,A的補碼就是f(B1)
---
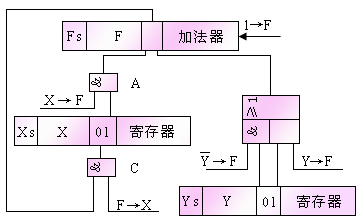
機器實現:
x-y = x-1-y+1 = (x-1) - y + 1
在補碼的轉碼中,這里的x=2^N
這里的(x-1) - y即使對y進行反碼操作,在ALU中可以N位同時刷新
至于N位整數+1,有一定的進位延時。
---
邊界情況:
容易看到,我們對-2^N求反,仍然是-2^N
對2^N-1求反,則是-(2^N)-1
---
利用補碼這種編碼性質
f(y) = -y
x + y = x + y
x - y = x + f(y)
---
馬后炮:事后猜測補碼發明的思路, 從而看補碼的優勢
先看正碼表示,設N=4, -1 = 1001; -2 = 1010, -1 》 -2, 但是 1001 《 1010,兩種映射的編碼的序性不一致
反碼呢,-1=1110, -2 = 1101, Ok,序性正確了,
然而,這里有一個問題,就是正數與負數之間,有一個1的縫隙。-1=1110, 1=0001,從循環編碼的角度,這兩個編碼相差3:1110-》1111-》0000-》0001。
因為正零和負零是兩個數,導致兩個數系的斷裂。怎么辦?讓負數整體往正數靠攏,邁進一步(+1),負1沒有了。
這就是求補的過程了。反碼再加1。
我想,當初寫出計算機的編碼設計論文的大牛(好像是圖靈還是什么的),當然有更深的考慮。但從序性和數系聯系的角度,補碼的發明是相當合理的。而這種合理性,我個人認為,正是其優點。
從機器實現的角度,并不算復雜,但相對反碼的機器實現,還是多了+1的進位延時。
---
int與unsigned int的思考
順便,我也整理一下這里的誤區。
如果聲明變量a為int,但是卻當作unsigned int,如果正常累加超出范圍,轉化成unsigned int結果應該還是可信的。
不過算了,我們利用好轉換和保證類型的一致,這些底層的問題我們確實還是當作透明為好。
-
補碼
+關注
關注
0文章
14瀏覽量
7541
發布評論請先 登錄
相關推薦
補碼是什么 補碼和原碼的轉化
補碼加、減運算規則
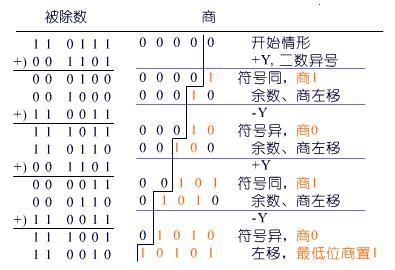
定點補碼一位除法的實現方案




 補碼是誰發明的_補碼有什么用
補碼是誰發明的_補碼有什么用











評論