編碼器
編碼器(encoder)是將信號(如比特流)或數(shù)據(jù)進行編制、轉(zhuǎn)換為可用以通訊、傳輸和存儲的信號形式的設(shè)備。編碼器把角位移或直線位移轉(zhuǎn)換成電信號,前者稱為碼盤,后者稱為碼尺。按照讀出方式編碼器可以分為接觸式和非接觸式兩種;按照工作原理編碼器可分為增量式和絕對式兩類。增量式編碼器是將位移轉(zhuǎn)換成周期性的電信號,再把這個電信號轉(zhuǎn)變成計數(shù)脈沖,用脈沖的個數(shù)表示位移的大小。絕對式編碼器的每一個位置對應(yīng)一個確定的數(shù)字碼,因此它的示值只與測量的起始和終止位置有關(guān),而與測量的中間過程無關(guān)。
格雷碼
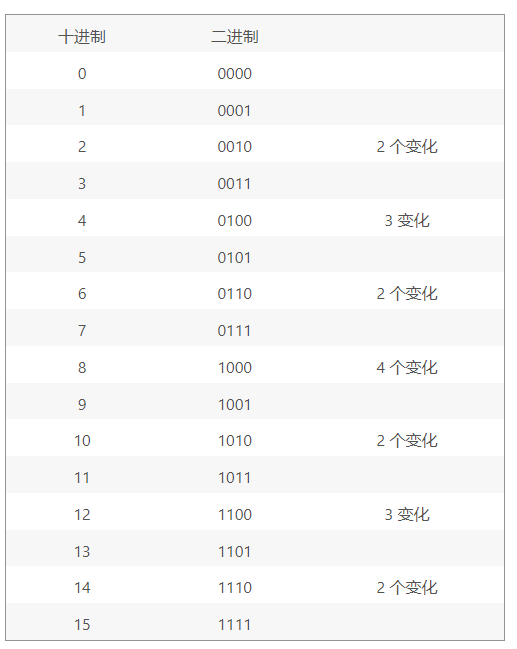
格雷碼屬于可靠性編碼,是一種錯誤最小化的編碼方式。因為,雖然自然二進制碼可以直接由數(shù)/模轉(zhuǎn)換器轉(zhuǎn)換成模擬信號,但在某些情況,例如從十進制的3轉(zhuǎn)換為4時二進制碼的每一位都要變,能使數(shù)字電路產(chǎn)生很大的尖峰電流脈沖。而格雷碼則沒有這一缺點,它在相鄰位間轉(zhuǎn)換時,只有一位產(chǎn)生變化。它大大地減少了由一個狀態(tài)到下一個狀態(tài)時邏輯的混淆。由于這種編碼相鄰的兩個碼組之間只有一位不同,因而在用于方向的轉(zhuǎn)角位移量-數(shù)字量的轉(zhuǎn)換中,當(dāng)方向的轉(zhuǎn)角位移量發(fā)生微小變化(而可能引起數(shù)字量發(fā)生變化時,格雷碼僅改變一位,這樣與其它編碼同時改變兩位或多位的情況相比更為可靠,即可減少出錯的可能性。
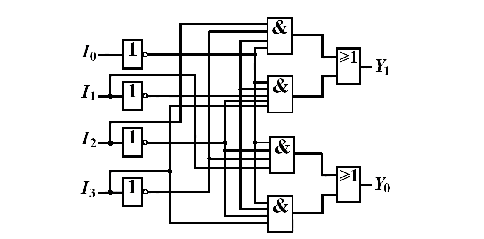
格雷碼的實現(xiàn)
格雷碼(Gray Code)是一個數(shù)列集合,每個數(shù)使用二進位來表示,假設(shè)使用n位元來表示每個數(shù)字,任兩個數(shù)之間只有一個位元值不同。
例如以下為3位元的格雷碼: 000 001 011 010 110 111 101 100 。
如果要產(chǎn)生n位元的格雷碼,那么格雷碼的個數(shù)為2^n.
假設(shè)原始的值從0開始,格雷碼產(chǎn)生的規(guī)律是:第一步,改變最右邊的位元值;第二步,改變右起第一個為1的位元的左邊位元;第三步,第四步重復(fù)第一步和第二步,直到所有的格雷碼產(chǎn)生完畢(換句話說,已經(jīng)走了(2^n) - 1 步)。
用一個例子來說明:
假設(shè)產(chǎn)生3位元的格雷碼,原始值位 000
第一步:改變最右邊的位元值: 001
第二步:改變右起第一個為1的位元的左邊位元: 011
第三步:改變最右邊的位元值: 010
第四步:改變右起第一個為1的位元的左邊位元: 110
第五步:改變最右邊的位元值: 111
第六步:改變右起第一個為1的位元的左邊位元: 101
第七步:改變最右邊的位元值: 100
如果按照這個規(guī)則來生成格雷碼,是沒有問題的,但是這樣做太復(fù)雜了。如果仔細觀察格雷碼的結(jié)構(gòu),我們會有以下發(fā)現(xiàn):
1、除了最高位(左邊第一位),格雷碼的位元完全上下對稱(看下面列表)。比如第一個格雷碼與最后一個格雷碼對稱(除了第一位),第二個格雷碼與倒數(shù)第二個對稱,以此類推。
2、最小的重復(fù)單元是 0 , 1。
000
001
011
010
110
111
101
100
所以,在實現(xiàn)的時候,我們完全可以利用遞歸,在每一層前面加上0或者1,然后就可以列出所有的格雷碼。
比如:
第一步:產(chǎn)生 0, 1 兩個字符串。
第二步:在第一步的基礎(chǔ)上,每一個字符串都加上0和1,但是每次只能加一個,所以得做兩次。這樣就變成了 00,01,11,10 (注意對稱)。
第三步:在第二步的基礎(chǔ)上,再給每個字符串都加上0和1,同樣,每次只能加一個,這樣就變成了 000,001,011,010,110,111,101,100。
好了,這樣就把3位元格雷碼生成好了。
如果要生成4位元格雷碼,我們只需要在3位元格雷碼上再加一層0,1就可以了: 0000,0001,0011,0010,0110,0111,0101,0100,1100,1101,1110,1010,0111,1001,1000.
也就是說,n位元格雷碼是基于n-1位元格雷碼產(chǎn)生的。
如果能夠理解上面的部分,下面部分的代碼實現(xiàn)就很容易理解了。
[java] view plain copypublic String[] GrayCode(int n) {
// produce 2^n grade codes
String[] graycode = new String[(int) Math.pow(2, n)];
if (n == 1) {
graycode[0] = “0”;
graycode[1] = “1”;
return graycode;
}
String[] last = GrayCode(n - 1);
for (int i = 0; i 《 last.length; i++) {
graycode[i] = “0” + last[i];
graycode[graycode.length - 1 - i] = “1” + last[i];
}
return graycode;
}
格雷碼還有一種實現(xiàn)方式是根據(jù)這個公式來的 G(n) = B(n) XOR B(n+1), 這也是格雷碼和二進制碼的轉(zhuǎn)換公式。代碼如下:
[java] view plain copypublic void getGrayCode(int bitNum){
for(int i = 0; i 《 (int)Math.pow(2, bitNum); i++){
int grayCode = (i 》》 1) ^ i;
System.out.println(num2Binary(grayCode, bitNum));
}
}
public String num2Binary(int num, int bitNum){
String ret = “”;
for(int i = bitNum-1; i 》= 0; i--){
ret += (num 》》 i) & 1;
}
return ret;
}
這是一道google 的面試題,以上代碼均是網(wǎng)友peking2 和 SEwind520寫成。原題還要求把二進制碼轉(zhuǎn)成十進制數(shù)。
-
編碼器
+關(guān)注
關(guān)注
45文章
3592瀏覽量
134145 -
格雷碼
+關(guān)注
關(guān)注
2文章
34瀏覽量
13175
發(fā)布評論請先 登錄
相關(guān)推薦
什么是格雷碼

編碼器的定義與功能 編碼器的工作原理和種類

常用編碼(BCD編碼、余3碼、格雷反射碼、奇偶校驗碼)
格雷碼簡介及格雷碼與二進制的轉(zhuǎn)換程序
格雷碼的規(guī)則和應(yīng)用問題?
編碼器的定義
格雷碼式旋轉(zhuǎn)編碼器在位移檢測中的應(yīng)用
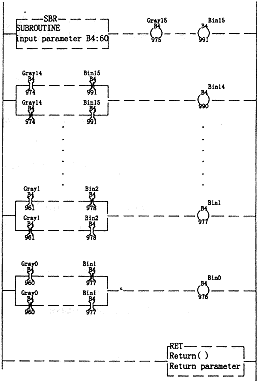




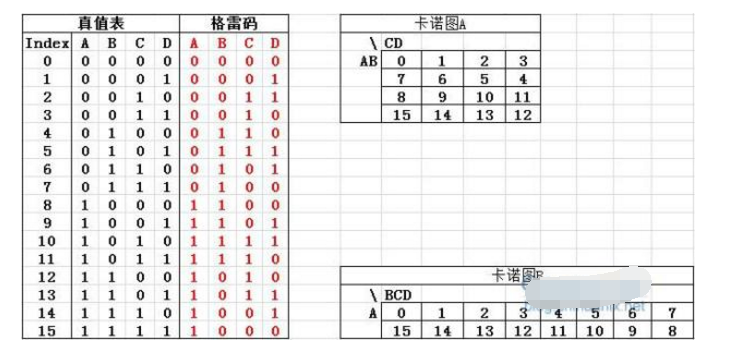
 格雷碼編碼器功能實現(xiàn)
格雷碼編碼器功能實現(xiàn)










評論