(一)一個框架看懂優化算法
“說到優化算法,入門級必從 SGD 學起,老司機則會告訴你更好的還有AdaGrad / AdaDelta,或者直接無腦用 Adam。可是看看學術界的最新 paper,卻發現一眾大神還在用著入門級的 SGD,最多加個 Momentum 或者Nesterov,還經常會黑一下 Adam。這是為什么呢?”
機器學習界有一群煉丹師,他們每天的日常是:
拿來藥材(數據),架起八卦爐(模型),點著六味真火(優化算法),就搖著蒲扇等著丹藥出爐了。
不過,當過廚子的都知道,同樣的食材,同樣的菜譜,但火候不一樣了,這出來的口味可是千差萬別。火小了夾生,火大了易糊,火不勻則半生半糊。
機器學習也是一樣,模型優化算法的選擇直接關系到最終模型的性能。有時候效果不好,未必是特征的問題或者模型設計的問題,很可能就是優化算法的問題。
說到優化算法,入門級必從 SGD 學起,老司機則會告訴你更好的還有 AdaGrad / AdaDelta,或者直接無腦用 Adam。可是看看學術界的最新 paper,卻發現一眾大神還在用著入門級的 SGD,最多加個 Momentum 或者 Nesterov,還經常會黑一下Adam。比如 UC Berkeley 的一篇論文就在 Conclusion 中寫道:
Despite the fact that our experimental evidence demonstrates that adaptive methods are not advantageous for machine learning, the Adam algorithm remains incredibly popular. We are not sure exactly as to why ……
無奈與酸楚之情溢于言表。
這是為什么呢?難道平平淡淡才是真?
▌01一個框架回顧優化算法
首先我們來回顧一下各類優化算法。
深度學習優化算法經歷了SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam這樣的發展歷程。Google一下就可以看到很多的教程文章,詳細告訴你這些算法是如何一步一步演變而來的。在這里,我們換一個思路,用一個框架來梳理所有的優化算法,做一個更加高屋建瓴的對比。
優化算法通用框架
首先定義:待優化參數:w ,目標函數: f(w),初始學習率α。而后,開始進行迭代優化。在每個epocht:
1. 計算目標函數關于當前參數的梯度:
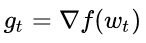
2. 根據歷史梯度計算一階動量和二階動量:
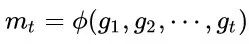
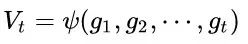
3. 計算當前時刻的下降梯度:
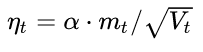
4. 根據下降梯度進行更新:
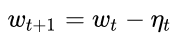
掌握了這個框架,你可以輕輕松松設計自己的優化算法。
我們拿著這個框架,來照一照各種玄乎其玄的優化算法的真身。步驟3、4對于各個算法都是一致的,主要的差別就體現在1和2上。
▌02固定學習率的優化算法
SGD
先來看SGD。SGD沒有動量的概念,也就是說:
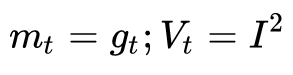
代入步驟3,可以看到下降梯度就是最簡單的
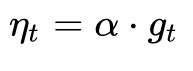
SGD最大的缺點是下降速度慢,而且可能會在溝壑的兩邊持續震蕩,停留在一個局部最優點。
SGD with Momentum
為了抑制SGD的震蕩,SGDM認為梯度下降過程可以加入慣性。下坡的時候,如果發現是陡坡,那就利用慣性跑的快一些。SGDM全稱是SGD with momentum,在SGD基礎上引入了一階動量:
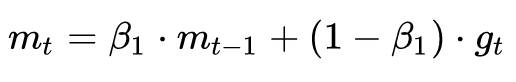
一階動量是各個時刻梯度方向的指數移動平均值,約等于最近 1/(1-β1)個時刻的梯度向量和的平均值。
也就是說,t 時刻的下降方向,不僅由當前點的梯度方向決定,而且由此前累積的下降方向決定。β1的經驗值為0.9,這就意味著下降方向主要是此前累積的下降方向,并略微偏向當前時刻的下降方向。想象高速公路上汽車轉彎,在高速向前的同時略微偏向,急轉彎可是要出事的。
SGD with Nesterov Acceleration
SGD 還有一個問題是困在局部最優的溝壑里面震蕩。想象一下你走到一個盆地,四周都是略高的小山,你覺得沒有下坡的方向,那就只能待在這里了。可是如果你爬上高地,就會發現外面的世界還很廣闊。因此,我們不能停留在當前位置去觀察未來的方向,而要向前一步、多看一步、看遠一些。
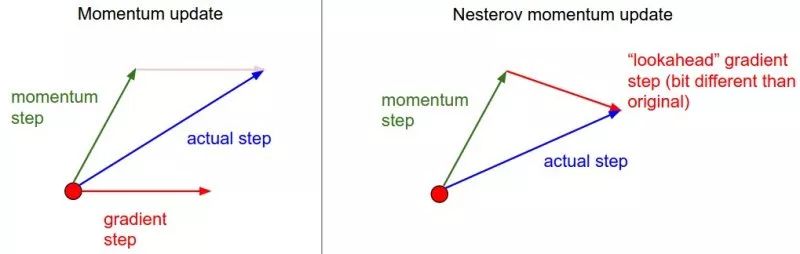
(source:http://cs231n.github.io/neural-networks-3)
這一方法也稱為NAG,即 Nesterov Accelerated Gradient,是在SGD、SGD-M 的基礎上的進一步改進,改進點在于步驟 1。我們知道在時刻 t 的主要下降方向是由累積動量決定的,自己的梯度方向說了也不算,那與其看當前梯度方向,不如先看看如果跟著累積動量走了一步,那個時候再怎么走。因此,NAG在步驟 1,不計算當前位置的梯度方向,而是計算如果按照累積動量走了一步,那個時候的下降方向:
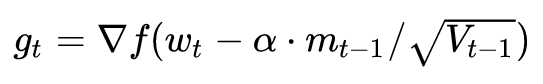
然后用下一個點的梯度方向,與歷史累積動量相結合,計算步驟 2 中當前時刻的累積動量。
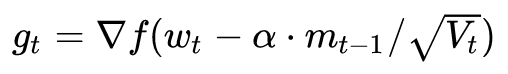
▌03自適應學習率的優化算法
此前我們都沒有用到二階動量。二階動量的出現,才意味著“自適應學習率”優化算法時代的到來。SGD及其變種以同樣的學習率更新每個參數,但深度神經網絡往往包含大量的參數,這些參數并不是總會用得到(想想大規模的embedding)。
對于經常更新的參數,我們已經積累了大量關于它的知識,不希望被單個樣本影響太大,希望學習速率慢一些;對于偶爾更新的參數,我們了解的信息太少,希望能從每個偶然出現的樣本身上多學一些,即學習速率大一些。
AdaGrad
怎么樣去度量歷史更新頻率呢?那就是二階動量——該維度上,迄今為止所有梯度值的平方和:
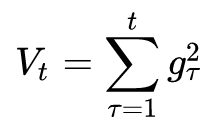
我們再回顧一下步驟3中的下降梯度:
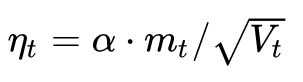
可以看出,此時實質上的學習率由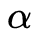 變成了
變成了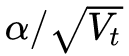 。 一般為了避免分母為0,會在分母上加一個小的平滑項。因此
。 一般為了避免分母為0,會在分母上加一個小的平滑項。因此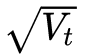 是恒大于0的,而且參數更新越頻繁,二階動量越大,學習率就越小。
是恒大于0的,而且參數更新越頻繁,二階動量越大,學習率就越小。
這一方法在稀疏數據場景下表現非常好。但也存在一些問題:因為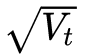 是單調遞增的,會使得學習率單調遞減至0,可能會使得訓練過程提前結束,即便后續還有數據也無法學到必要的知識。
是單調遞增的,會使得學習率單調遞減至0,可能會使得訓練過程提前結束,即便后續還有數據也無法學到必要的知識。
AdaDelta / RMSProp
由于AdaGrad單調遞減的學習率變化過于激進,我們考慮一個改變二階動量計算方法的策略:不累積全部歷史梯度,而只關注過去一段時間窗口的下降梯度。這也就是AdaDelta名稱中Delta的來歷。
修改的思路很簡單。前面我們講到,指數移動平均值大約就是過去一段時間的平均值,因此我們用這一方法來計算二階累積動量:
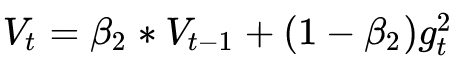
這就避免了二階動量持續累積、導致訓練過程提前結束的問題了。
Adam
談到這里,Adam和Nadam的出現就很自然而然了——它們是前述方法的集大成者。我們看到,SGD-M在SGD基礎上增加了一階動量,AdaGrad和AdaDelta在SGD基礎上增加了二階動量。把一階動量和二階動量都用起來,就是Adam了——Adaptive + Momentum。
SGD的一階動量:
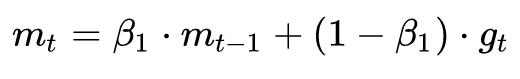
加上AdaDelta的二階動量:
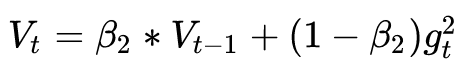
優化算法里最常見的兩個超參數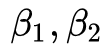 就都在這里了,前者控制一階動量,后者控制二階動量。
就都在這里了,前者控制一階動量,后者控制二階動量。
Nadam
最后是Nadam。我們說Adam是集大成者,但它居然遺漏了Nesterov,這還能忍?必須給它加上——只需要按照NAG的步驟1來計算梯度:
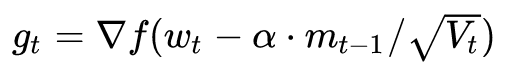
這就是Nesterov + Adam = Nadam了。
說到這里,大概可以理解為什么說 Adam / Nadam 目前最主流、最好用的算法了。無腦用Adam/Nadam,收斂速度嗖嗖滴,效果也是杠杠滴。
那為什么Adam還老招人黑,被學術界一頓鄙夷?難道只是為了發paper灌水嗎?
(二)Adam的兩宗罪
“一代又一代的研究者們為了我們能煉(xun)好(hao)金(mo)丹(xing)可謂是煞費苦心。從理論上看,一代更比一代完善,Adam/Nadam已經登峰造極了,為什么大家還是不忘初心SGD呢?”
以上內容中,我們用一個框架來回顧了主流的深度學習優化算法。可以看到,一代又一代的研究者們為了我們能煉(xun)好(hao)金(mo)丹(xing)可謂是煞費苦心。從理論上看,一代更比一代完善,Adam/Nadam已經登峰造極了,為什么大家還是不忘初心SGD呢?
舉個栗子。很多年以前,攝影離普羅大眾非常遙遠。十年前,傻瓜相機開始風靡,游客幾乎人手一個。智能手機出現以后,攝影更是走進千家萬戶,手機隨手一拍,前后兩千萬,照亮你的美(咦,這是什么亂七八糟的)。但是專業攝影師還是喜歡用單反,孜孜不倦地調光圈、快門、ISO、白平衡……一堆自拍黨從不care的名詞。技術的進步,使得傻瓜式操作就可以得到不錯的效果,但是在特定的場景下,要拍出最好的效果,依然需要深入地理解光線、理解結構、理解器材。
優化算法大抵也如此。在上一篇中,我們用同一個框架讓各類算法對號入座。可以看出,大家都是殊途同歸,只是相當于在SGD基礎上增加了各類學習率的主動控制。如果不想做精細的調優,那么Adam顯然最便于直接拿來上手。
但這樣的傻瓜式操作并不一定能夠適應所有的場合。如果能夠深入了解數據,研究員們可以更加自如地控制優化迭代的各類參數,實現更好的效果也并不奇怪。畢竟,精調的參數還比不過傻瓜式的SGD,無疑是在挑戰頂級研究員們的煉丹經驗!
最近,不少paper開懟Adam,我們簡單看看都在說什么:
▌04Adam罪狀一:可能不收斂
這篇是正在深度學習領域頂級會議之一 ICLR 2018 匿名審稿中的一篇論文《On the Convergence of Adam and Beyond》,探討了Adam算法的收斂性,通過反例證明了Adam在某些情況下可能會不收斂。
回憶一下上文提到的各大優化算法的學習率:
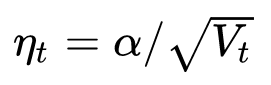
其中,SGD沒有用到二階動量,因此學習率是恒定的(實際使用過程中會采用學習率衰減策略,因此學習率遞減)。AdaGrad的二階動量不斷累積,單調遞增,因此學習率是單調遞減的。因此,這兩類算法會使得學習率不斷遞減,最終收斂到0,模型也得以收斂。
但AdaDelta和Adam則不然。二階動量是固定時間窗口內的累積,隨著時間窗口的變化,遇到的數據可能發生巨變,使得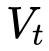 可能會時大時小,不是單調變化。這就可能在訓練后期引起學習率的震蕩,導致模型無法收斂。
可能會時大時小,不是單調變化。這就可能在訓練后期引起學習率的震蕩,導致模型無法收斂。
這篇文章也給出了一個修正的方法。由于Adam中的學習率主要是由二階動量控制的,為了保證算法的收斂,可以對二階動量的變化進行控制,避免上下波動。
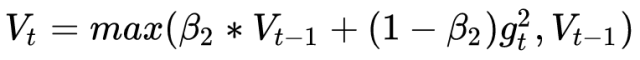
通過這樣修改,就保證了
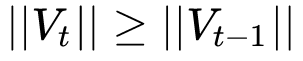
從而使得學習率單調遞減。
▌05Adam罪狀二:可能錯過全局最優解
深度神經網絡往往包含大量的參數,在這樣一個維度極高的空間內,非凸的目標函數往往起起伏伏,擁有無數個高地和洼地。有的是高峰,通過引入動量可能很容易越過;但有些是高原,可能探索很多次都出不來,于是停止了訓練。
之前,Arxiv上的兩篇文章談到這個問題。
第一篇就是前文提到的吐槽Adam最狠的UC Berkeley的文章《The Marginal Value of Adaptive Gradient Methods in Machine Learning》。文中說到,同樣的一個優化問題,不同的優化算法可能會找到不同的答案,但自適應學習率的算法往往找到非常差的答案(very poor solution)。他們設計了一個特定的數據例子,自適應學習率算法可能會對前期出現的特征過擬合,后期才出現的特征很難糾正前期的擬合效果。但這個文章給的例子很極端,在實際情況中未必會出現。
另外一篇是《Improving Generalization Performance by Switching from Adam to SGD》,進行了實驗驗證。他們CIFAR-10數據集上進行測試,Adam的收斂速度比SGD要快,但最終收斂的結果并沒有SGD好。他們進一步實驗發現,主要是后期Adam的學習率太低,影響了有效的收斂。他們試著對Adam的學習率的下界進行控制,發現效果好了很多。
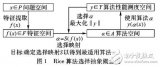
于是他們提出了一個用來改進Adam的方法:前期用Adam,享受Adam快速收斂的優勢;后期切換到SGD,慢慢尋找最優解。這一方法以前也被研究者們用到,不過主要是根據經驗來選擇切換的時機和切換后的學習率。這篇文章把這一切換過程傻瓜化,給出了切換SGD的時機選擇方法,以及學習率的計算方法,效果看起來也不錯。
這個算法挺有趣,下一篇我們可以來談談,這里先貼個算法框架圖:

▌06到底該用Adam還是SGD?
所以,談到現在,到底Adam好還是SGD好?這可能是很難一句話說清楚的事情。去看學術會議中的各種paper,用SGD的很多,Adam的也不少,還有很多偏愛AdaGrad或者AdaDelta。可能研究員把每個算法都試了一遍,哪個出來的效果好就用哪個了。畢竟paper的重點是突出自己某方面的貢獻,其他方面當然是無所不用其極,怎么能輸在細節上呢?
而從這幾篇怒懟Adam的paper來看,多數都構造了一些比較極端的例子來演示了Adam失效的可能性。這些例子一般過于極端,實際情況中可能未必會這樣,但這提醒了我們,理解數據對于設計算法的必要性。優化算法的演變歷史,都是基于對數據的某種假設而進行的優化,那么某種算法是否有效,就要看你的數據是否符合該算法的胃口了。
算法固然美好,數據才是根本。
另一方面,Adam之流雖然說已經簡化了調參,但是并沒有一勞永逸地解決問題,默認的參數雖然好,但也不是放之四海而皆準。因此,在充分理解數據的基礎上,依然需要根據數據特性、算法特性進行充分的調參實驗。
少年,好好煉丹吧。
(三)優化算法的選擇與使用策略
“ 在前面兩篇文章中,我們用一個框架梳理了各大優化算法,并且指出了以 Adam 為代表的自適應學習率優化算法可能存在的問題。那么,在實踐中我們應該如何選擇呢?本文介紹 Adam + SGD 的組合策略,以及一些比較有用的 tricks.”
▌07不同算法的核心差異:下降方向
從第一篇的框架中我們看到,不同優化算法最核心的區別,就是第三步所執行的下降方向:
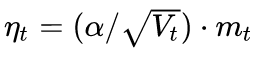
這個式子中,前半部分是實際的學習率(也即下降步長),后半部分是實際的下降方向。SGD算法的下降方向就是該位置的梯度方向的反方向,帶一階動量的SGD的下降方向則是該位置的一階動量方向。自適應學習率類優化算法為每個參數設定了不同的學習率,在不同維度上設定不同步長,因此其下降方向是縮放過(scaled)的一階動量方向。
由于下降方向的不同,可能導致不同算法到達完全不同的局部最優點。《An empirical analysis of the optimization of deep network loss surfaces》這篇論文中做了一個有趣的實驗,他們把目標函數值和相應的參數形成的超平面映射到一個三維空間,這樣我們可以直觀地看到各個算法是如何尋找超平面上的最低點的。
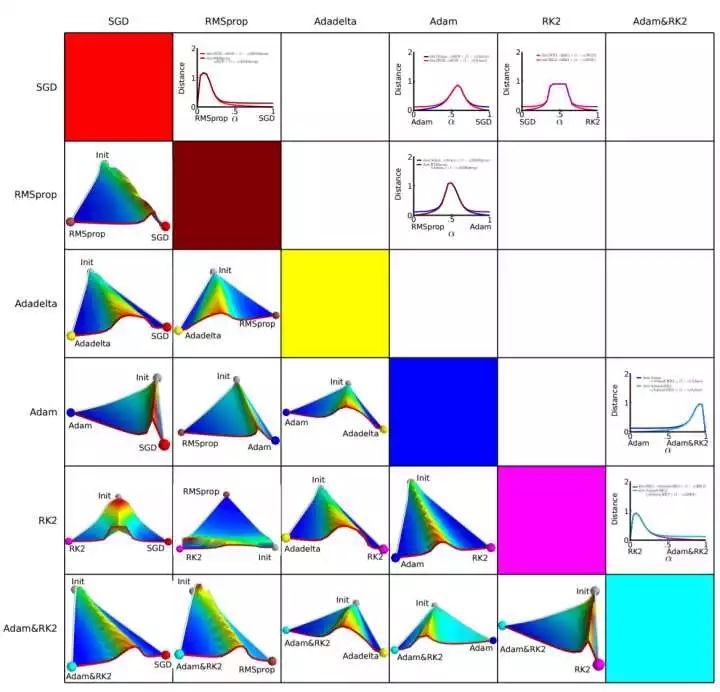
上圖是論文的實驗結果,橫縱坐標表示降維后的特征空間,區域顏色則表示目標函數值的變化,紅色是高原,藍色是洼地。他們做的是配對兒實驗,讓兩個算法從同一個初始化位置開始出發,然后對比優化的結果。可以看到,幾乎任何兩個算法都走到了不同的洼地,他們中間往往隔了一個很高的高原。這就說明,不同算法在高原的時候,選擇了不同的下降方向。
▌08Adam+SGD 組合策略
正是在每一個十字路口的選擇,決定了你的歸宿。如果上天能夠給我一個再來一次的機會,我會對那個女孩子說:SGD!
不同優化算法的優劣依然是未有定論的爭議話題。據我在paper和各類社區看到的反饋,主流的觀點認為:Adam等自適應學習率算法對于稀疏數據具有優勢,且收斂速度很快;但精調參數的SGD(+Momentum)往往能夠取得更好的最終結果。
那么我們就會想到,可不可以把這兩者結合起來,先用Adam快速下降,再用SGD調優,一舉兩得?思路簡單,但里面有兩個技術問題:
什么時候切換優化算法?——如果切換太晚,Adam可能已經跑到自己的盆地里去了,SGD再怎么好也跑不出來了。
切換算法以后用什么樣的學習率?——Adam用的是自適應學習率,依賴的是二階動量的累積,SGD接著訓練的話,用什么樣的學習率?
上一篇中提到的論文Improving Generalization Performance by Switching from Adam to SGD提出了解決這兩個問題的思路。
首先來看第二個問題,切換之后的學習率。
Adam的下降方向是
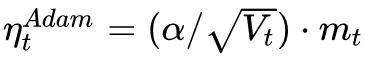
而SGD的下降方向是
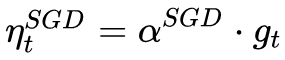
SGD下降方向必定可以分解為Adam下降方向及其正交方向上的兩個方向之和,那么其在Adam下降方向上的投影就意味著SGD在Adam算法決定的下降方向上前進的距離,而在Adam下降方向的正交方向上的投影是 SGD 在自己選擇的修正方向上前進的距離。
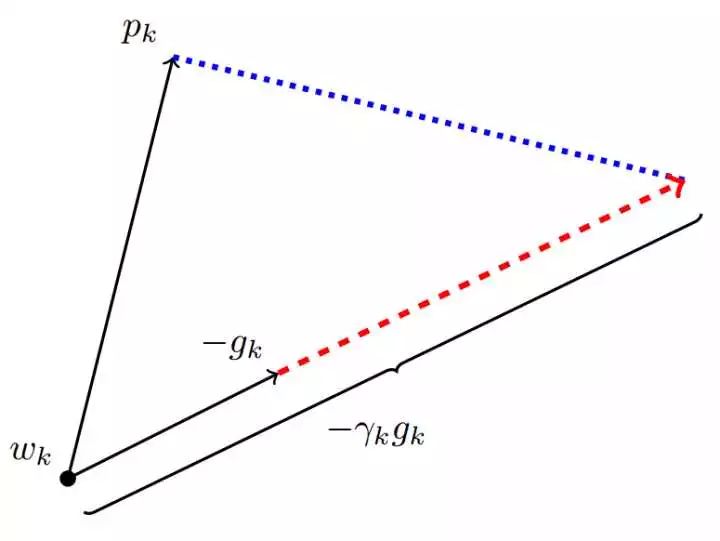
(圖片來自原文,這里p為Adam下降方向,g為梯度方向,r為SGD的學習率。)
如果SGD要走完Adam未走完的路,那就首先要接過Adam的大旗——沿著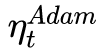 方向走一步,而后在沿著其正交方向走相應的一步。
方向走一步,而后在沿著其正交方向走相應的一步。
這樣我們就知道該如何確定SGD的步長(學習率)了——SGD在Adam下降方向上的正交投影,應該正好等于Adam的下降方向(含步長)。也即:
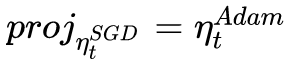
解這個方程,我們就可以得到接續進行SGD的學習率:
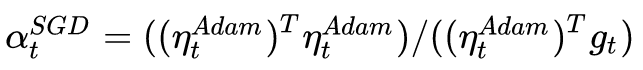
為了減少噪聲影響,我們可以使用移動平均值來修正對學習率的估計:
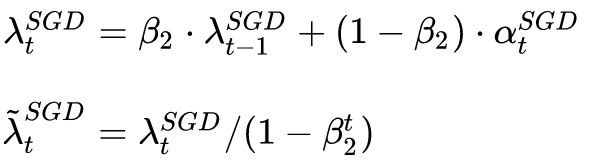
這里直接復用了Adam的 beta 參數。
然后來看第一個問題,何時進行算法的切換。
作者提出的方法很簡單,那就是當 SGD的相應學習率的移動平均值基本不變的時候,即:
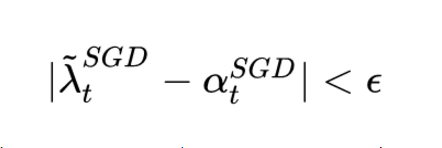
每次迭代完都計算一下SGD接班人的相應學習率,如果發現基本穩定了,那就SGD以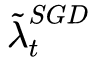 為學習率接班前進。不過,這一時機是不是最優的切換時機,作者并沒有給出數學證明,只是通過實驗驗證了效果,切換時機還是一個很值得深入研究的話題。
為學習率接班前進。不過,這一時機是不是最優的切換時機,作者并沒有給出數學證明,只是通過實驗驗證了效果,切換時機還是一個很值得深入研究的話題。
▌09優化算法的常用tricks
最后,分享一些在優化算法的選擇和使用方面的一些tricks。
1.首先,各大算法孰優孰劣并無定論。
如果是剛入門,優先考慮SGD+Nesterov Momentum或者Adam.(Standford 231n:The two recommended updates to use are either SGD+Nesterov Momentum or Adam)
2. 選擇你熟悉的算法——這樣你可以更加熟練地利用你的經驗進行調參。
3.充分了解你的數據——如果模型是非常稀疏的,那么優先考慮自適應學習率的算法。
4. 根據你的需求來選擇——在模型設計實驗過程中,要快速驗證新模型的效果,可以先用Adam進行快速實驗優化;在模型上線或者結果發布前,可以用精調的SGD進行模型的極致優化。
5. 先用小數據集進行實驗。有論文研究指出,隨機梯度下降算法的收斂速度和數據集的大小的關系不大。(The mathematics of stochastic gradient descent are amazingly independent of the training set size. In particular, the asymptotic SGD convergence rates are independent from the sample size. [2])因此可以先用一個具有代表性的小數據集進行實驗,測試一下最好的優化算法,并通過參數搜索來尋找最優的訓練參數。
6. 考慮不同算法的組合。先用Adam進行快速下降,而后再換到SGD進行充分的調優。切換策略可以參考本文介紹的方法。
7. 數據集一定要充分的打散(shuffle)。這樣在使用自適應學習率算法的時候,可以避免某些特征集中出現,而導致的有時學習過度、有時學習不足,使得下降方向出現偏差的問題。
8. 訓練過程中持續監控訓練數據和驗證數據上的目標函數值以及精度或者AUC等指標的變化情況。對訓練數據的監控是要保證模型進行了充分的訓練——下降方向正確,且學習率足夠高;對驗證數據的監控是為了避免出現過擬合。
9. 制定一個合適的學習率衰減策略。可以使用定期衰減策略,比如每過多少個epoch就衰減一次;或者利用精度或者AUC等性能指標來監控,當測試集上的指標不變或者下跌時,就降低學習率。
這里只列舉出一些在優化算法方面的trick,如有遺漏,歡迎各位在評論中補充。提前致謝!
-
優化算法
+關注
關注
0文章
35瀏覽量
9667 -
機器學習
+關注
關注
66文章
8377瀏覽量
132406
原文標題:Adam那么棒,為什么還對SGD念念不忘
文章出處:【微信號:AI_Thinker,微信公眾號:人工智能頭條】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
《MATLAB優化算法案例分析與應用》
工業相機硬觸發?光源閃頻?視覺算法優化?雙ccd框架怎么寫?編程沒頭緒?labview雙ccd框架,拯救你的發量!
KeenTune的算法之心——KeenOpt 調優算法框架 | 龍蜥技術
一個新的二進前向多層網學習算法及布爾函數優化實現
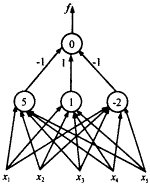
一文看懂常用的梯度下降算法
人工魚群算法應用于飼料配方優化
基于Spark框架與聚類優化的高效KNN分類算法
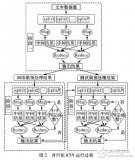
增量流形學習正則優化算法
使用MATLAB遺傳算法實現弧形閘門主框架優化設計的詳細資料說明





 一個框架看懂優化算法
一個框架看懂優化算法










評論