線性系統(tǒng)是什么
線性系統(tǒng)是指同時滿足疊加性與均勻性(又稱為其次性)的系統(tǒng)。所謂疊加性是指當幾個輸入信號共同作用于系統(tǒng)時,總的輸出等于每個輸入單獨作用時產(chǎn)生的輸出之和;均勻性是指當輸入信號增大若干倍時,輸出也相應增大同樣的倍數(shù)。對于線性連續(xù)控制系統(tǒng),可以用線性的微分方程來表示。不滿足疊加性和均勻性的系統(tǒng)即為非線性系統(tǒng) 。
由于線性系統(tǒng)較容易處理,許多時候會將系統(tǒng)理想化或簡化為線性系統(tǒng)。線性系統(tǒng)常應用在自動控制理論、信號處理及電信上。像無線通訊訊號在介質(zhì)中的傳播就可以用線性系統(tǒng)來模擬。
線性系統(tǒng)的函數(shù)表達為

如圖:
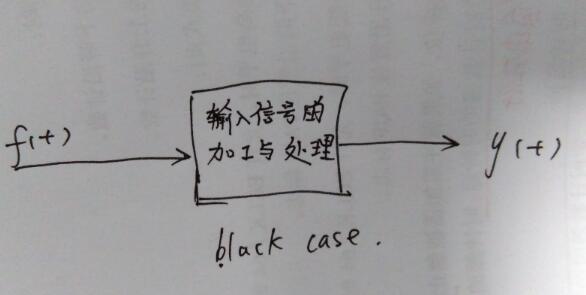
線性系統(tǒng)和非線性系統(tǒng)的區(qū)別
如果從系統(tǒng)狀態(tài)空間表達式來觀察,線性系統(tǒng)和非線性系統(tǒng)最明顯的區(qū)別方法就是線性系統(tǒng)遵從疊加原理,而非線性系統(tǒng)不然。
所謂疊加原理舉個例子就是:
f(x)=2x,f(y)=2y,f(x+y)=2(x+y)=2x+2y=f(x)+f(y)
舉個反例:
f(x)=2x^2,f(y)=2y^2,f(x)+f(y)=2(x^2+y^2),但f(x+y)=2(x+y)^2,兩個顯然不等。
換句話說,線性系統(tǒng)的表達式中只有狀態(tài)變量的一次項,高次、三角函數(shù)以及常數(shù)項都沒有,只要有任意一個非線性環(huán)節(jié)就是非線性系統(tǒng)。
判斷線性系統(tǒng)的例題
判斷下述微分方程所對應的系統(tǒng)是否為線性系統(tǒng)?
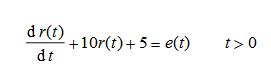
分析:
1)均勻性
設信號e(t)作用系統(tǒng),響應為r(t)。當激勵Ae(t)作用于系統(tǒng)時,根據(jù)描述系統(tǒng)的微分方程,將方程兩邊乘以A,得到
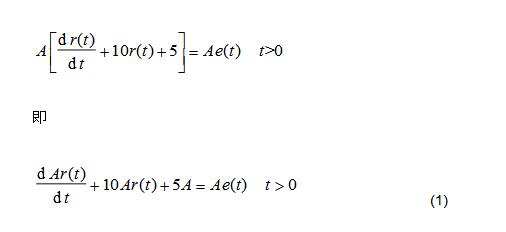
這是先經(jīng)系統(tǒng),再線性運算的結果。
下面討論先線性運算,再經(jīng)系統(tǒng)的結果。顯然線性運算后的激勵為Ae(t)。而若系統(tǒng)具有均勻性的話,根據(jù)描述系統(tǒng)的微分方程,所得結果應該是
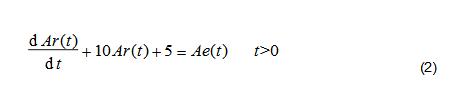
顯然式(1)不等于式(2),即系統(tǒng)不滿足均勻性。
2)疊加性
假設兩個激勵分別為e1(t)和e2(t),其相應的響應分別為r1(t)和r2(t)。根據(jù)描述系統(tǒng)的微分方程,有下列關系成立。

這是先經(jīng)系統(tǒng),再線性運算的結果。
下面討論先線性運算,再經(jīng)系統(tǒng)的結果。顯然線性運算后的激勵為e1(t)+e2(t)。而若系統(tǒng)滿足疊加性的話,根據(jù)描述系統(tǒng)的微分方程,所得結果應該是
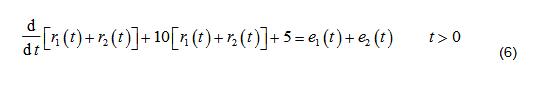
顯然式(5)不等于式(6),即系統(tǒng)不滿足疊加性。
由1)和2)中的結論得知,該系統(tǒng)既不滿足均勻性,也不滿足疊加性,顯然是非線性系統(tǒng)。
延伸閱讀:
-
線性
+關注
關注
0文章
196瀏覽量
25128 -
線性系統(tǒng)
+關注
關注
0文章
43瀏覽量
14688
發(fā)布評論請先 登錄
相關推薦
線性系統(tǒng)的設計與綜合
線性系統(tǒng)的狀態(tài)空間描述
線性系統(tǒng)狀態(tài)轉(zhuǎn)移矩陣討論
線性系統(tǒng)理論幻燈片
如何判斷差分方程描述的系統(tǒng)的線性和時變性?《數(shù)字信號處理》考研題
如何分析判斷系統(tǒng)是否為穩(wěn)定系統(tǒng)、因果系統(tǒng)、線性系統(tǒng)?

如何判斷是否為線性電阻
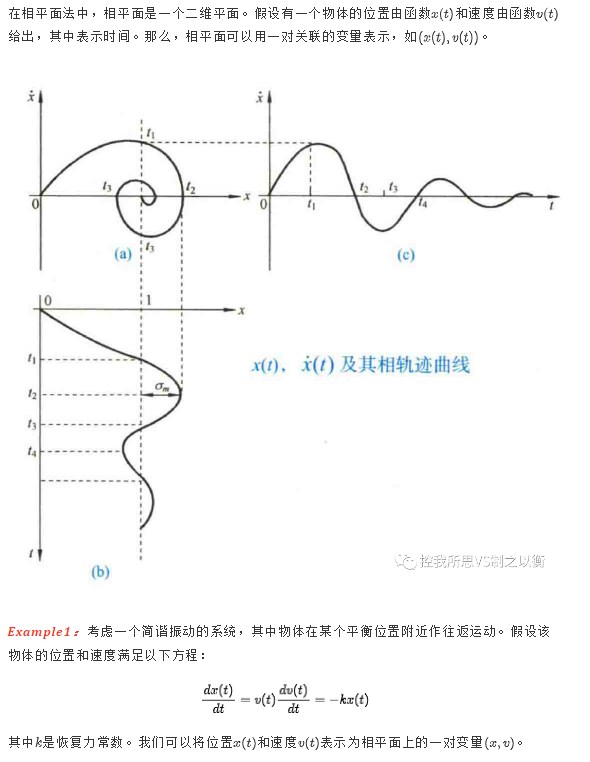
淺析非線性系統(tǒng)的相平面法




 如何判斷系統(tǒng)是否線性_判斷線性系統(tǒng)簡單方法
如何判斷系統(tǒng)是否線性_判斷線性系統(tǒng)簡單方法
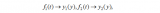










評論