一般來(lái)說(shuō),圖形是基本的數(shù)據(jù)結(jié)構(gòu),它在諸如知識(shí)圖、物理和社會(huì)交互、語(yǔ)言和化學(xué)等許多重要的實(shí)際領(lǐng)域中對(duì)關(guān)系結(jié)構(gòu)進(jìn)行簡(jiǎn)明地捕捉。在本文中,我們引入了一種強(qiáng)大的新方法,用于學(xué)習(xí)圖形中的生成式模型,既可以捕捉它們的結(jié)構(gòu)也可以捕捉到屬性。我們的方法使用圖形神經(jīng)網(wǎng)絡(luò)表示圖形節(jié)點(diǎn)和邊緣之間的概率依賴(lài)關(guān)系,并且原則上來(lái)說(shuō),可以學(xué)習(xí)任何任意圖形上的分布。經(jīng)過(guò)一系列實(shí)驗(yàn),我們的結(jié)果顯示,一旦經(jīng)過(guò)訓(xùn)練之后,我們的模型可以生成高質(zhì)量的合成圖和真實(shí)分子圖的樣本,無(wú)論是在無(wú)條件數(shù)據(jù)還是條件數(shù)據(jù)的情況下都是如此。與不使用圖形結(jié)構(gòu)表示的基線(xiàn)相比,我們的模型通常表現(xiàn)得更好。我們還探索了學(xué)習(xí)圖形生成式模型過(guò)程中所存在的關(guān)鍵性挑戰(zhàn),例如,如何在圖形生成過(guò)程中處理元素的對(duì)稱(chēng)性和排序,并提供可能的解決方案。可以這樣說(shuō),我們的研究是用于學(xué)習(xí)任意圖形上生成式模型的第一個(gè)方法,也是最為通用的方法,并且為從向量和序列式的知識(shí)表示,轉(zhuǎn)向更有表現(xiàn)力和更靈活的關(guān)系數(shù)據(jù)結(jié)構(gòu),開(kāi)辟了新的研究方向。
圖形是許多問(wèn)題域中信息的本質(zhì)性表示。例如,知識(shí)圖表和社交網(wǎng)絡(luò)中的實(shí)體之間的關(guān)系可以很好地用圖形進(jìn)行表示,而且它們也適用于對(duì)物理世界進(jìn)行建模,例如,分子結(jié)構(gòu)以及物理系統(tǒng)中物體之間的交互。因此,捕捉特定圖形族系分布的能力在實(shí)際生活中有很多應(yīng)用。例如,從圖形模型中進(jìn)行采樣可以致使發(fā)現(xiàn)新的配置,而這些配置所具有的全局屬性與藥物發(fā)現(xiàn)中所需要的是一樣的(Gómez-Bombarelli等人于2016年提出)。要想獲得自然語(yǔ)言句子中的圖形結(jié)構(gòu)語(yǔ)義表示(Kuhlmann和Oepen于2016年提出),需要具有能夠在圖上對(duì)(條件)分布進(jìn)行建模的能力。圖形上的分布還可以為圖形模型的貝葉斯結(jié)構(gòu)學(xué)習(xí)提供先驗(yàn)(Margaritis于2003年提出)。
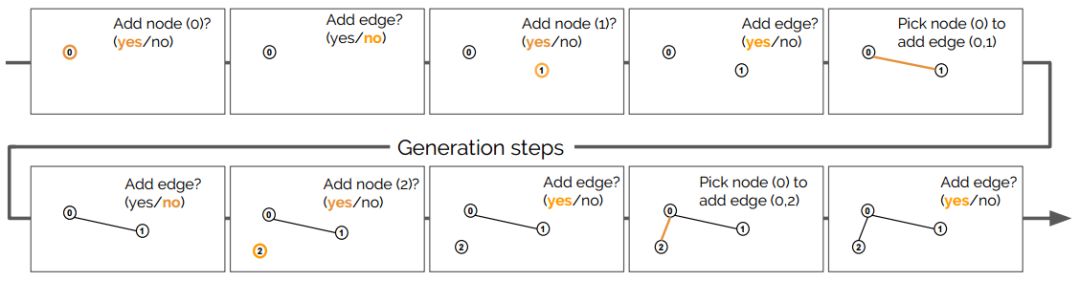
生成過(guò)程中所采取步驟的描述
我們至少?gòu)膬蓚€(gè)角度對(duì)圖形的概率模型進(jìn)行了廣泛研究。一種方法是基于隨機(jī)圖形模型,將概率分配給大的圖形類(lèi)型(Erdos和Rényi于1960年、Barabási和Albert于1999年提出)。這些都具有很強(qiáng)的獨(dú)立性假設(shè),并且被設(shè)計(jì)成僅捕捉某些特定的圖形屬性,例如度數(shù)分布(degree distribution)和直徑。雖然這些方法已被證明在對(duì)社交網(wǎng)絡(luò)等領(lǐng)域進(jìn)行建模時(shí)是有效的,但它們?cè)诟迂S富的結(jié)構(gòu)化領(lǐng)域上應(yīng)用還存在很大的挑戰(zhàn),其中,細(xì)微的結(jié)構(gòu)差異在功能上可能是具有重要意義的,例如在化學(xué)中領(lǐng)域或自然語(yǔ)言中所表示的意義。
一個(gè)更具表現(xiàn)力但也更為脆弱的方法則是使用圖形語(yǔ)法,它將機(jī)制從形式語(yǔ)言理論中泛化到非序列結(jié)構(gòu)模型中(Rozenberg于1997年提出)。圖語(yǔ)法是重寫(xiě)規(guī)則的系統(tǒng),通過(guò)中間圖的一系列轉(zhuǎn)換遞增地導(dǎo)出輸出圖。雖然符號(hào)圖形語(yǔ)法(symbolic graph grammars)可以使用標(biāo)準(zhǔn)技術(shù)進(jìn)行隨機(jī)化或加權(quán)(Droste和Gastin于2007年提出),但從可學(xué)習(xí)性的觀(guān)點(diǎn)來(lái)看,仍然存在兩個(gè)需要解決的問(wèn)題。首先,從一組未經(jīng)注釋的圖形中引入語(yǔ)法是非常重要的,因?yàn)橐雽?duì)可能用于構(gòu)建圖形的結(jié)構(gòu)構(gòu)建操作進(jìn)行理解在算法上是很難進(jìn)行的(Lautemann于1988年、Agui?aga等人于2016年提出)。其次,與線(xiàn)性輸出語(yǔ)法一樣,圖形語(yǔ)法在語(yǔ)言?xún)?nèi)容和要排除內(nèi)容之間的區(qū)分上存在很大的困難,使得這種模型對(duì)于一些應(yīng)用程序來(lái)說(shuō)是不適合應(yīng)用的,其中,它不適合將0概率分配給某些特定圖形。
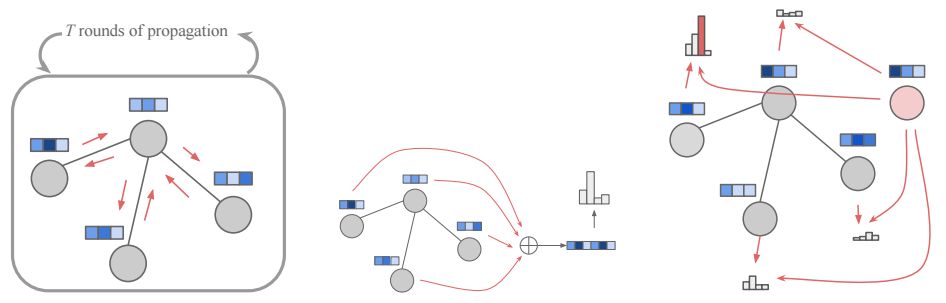
圖形傳播過(guò)程的示意圖(左),節(jié)點(diǎn)選擇 fnodes模塊(右)
本文引入了一種新的、富有表現(xiàn)力的圖形模型,它不需要做任何結(jié)構(gòu)性假設(shè),也避免了基于語(yǔ)法的技術(shù)的脆弱性。我們的模型以類(lèi)似于圖形語(yǔ)法的方式生成圖形,其中在導(dǎo)出過(guò)程中,新結(jié)構(gòu)(特別是新節(jié)點(diǎn)或新邊緣)被添加到現(xiàn)有圖形中,并且該添加事件的概率取決于圖形導(dǎo)出的歷史記錄。為了在導(dǎo)出的每個(gè)步驟中對(duì)圖形進(jìn)行表示,我們使用一個(gè)基于圖形結(jié)構(gòu)的神經(jīng)網(wǎng)絡(luò)(圖形網(wǎng)絡(luò))表示。最近,人們對(duì)于用于學(xué)習(xí)圖形表示和解決圖形預(yù)測(cè)問(wèn)題的圖形網(wǎng)絡(luò)(graph nets)很感興趣。這些模型是根據(jù)所利用的圖形進(jìn)行構(gòu)造的,并且以獨(dú)立于圖形大小的方式進(jìn)行參數(shù)化,因此針對(duì)同構(gòu)圖形具有不變性,從而為我們的研究目的提供了一個(gè)很好的匹配。
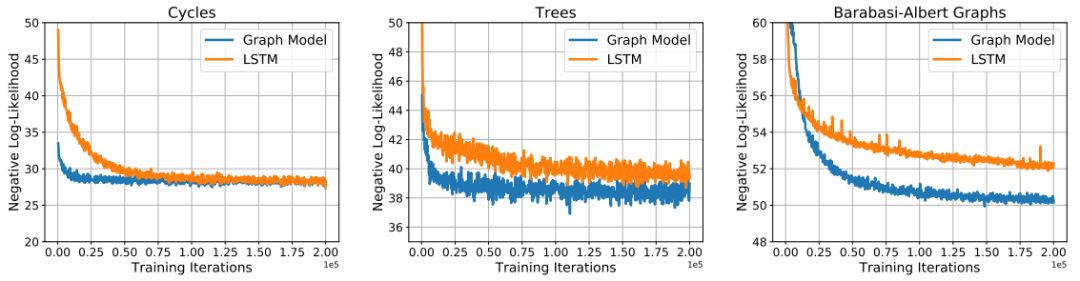
在三組數(shù)據(jù)集中對(duì)圖形模型和LSTM模型進(jìn)行訓(xùn)練的曲線(xiàn)
我們?cè)谏删哂心承┏R?jiàn)拓?fù)湫再|(zhì)(例如:周期性)的隨機(jī)圖形,和以非條件或條件的方式生成分子圖形的任務(wù)中對(duì)我們的模型進(jìn)行了評(píng)估。我們提出的模型在所有的實(shí)驗(yàn)中都表現(xiàn)良好,并且比隨機(jī)圖形模型(random graph models)和長(zhǎng)短期記憶網(wǎng)絡(luò)基線(xiàn)(LSTM baselines)獲得了更好的結(jié)果。
本文所提出的是能夠生成任意圖形的強(qiáng)大模型。然而,這些模型依然面臨著許多挑戰(zhàn)。在本文中,我們將討論未來(lái)會(huì)面臨的一些挑戰(zhàn)及可能的解決方案。
排序
節(jié)點(diǎn)和邊緣的排序?qū)τ趯W(xué)習(xí)和評(píng)估而言都很重要,在實(shí)驗(yàn)中,我們總是使用預(yù)定義的分配方式排序。然而,通過(guò)將排序π視為潛在的變量來(lái)學(xué)習(xí)節(jié)點(diǎn)和邊緣的排序也許是可能的,這在未來(lái)將是一個(gè)有趣的探索方向。
長(zhǎng)序列
圖形模型所使用的生成過(guò)程通常是一個(gè)長(zhǎng)的決策序列,如果其他形式的圖形線(xiàn)性化是可用的(例如:SMILES),那么這樣的序列通常會(huì)縮短2-3倍。這對(duì)于圖形模型而言是一個(gè)很大的劣勢(shì),這不僅難以獲得準(zhǔn)確的概率,還會(huì)使訓(xùn)練變得更加困難。為了緩解這一問(wèn)題,我們可以調(diào)整圖形模型,以便使其與問(wèn)題域進(jìn)行更多地關(guān)聯(lián),從而將多個(gè)決策步驟和循環(huán)轉(zhuǎn)為單個(gè)步驟。
可擴(kuò)展性
可擴(kuò)展性是對(duì)本文所提出的圖形生成模型的一個(gè)挑戰(zhàn)。圖形網(wǎng)絡(luò)使用固定的傳播步驟T來(lái)上傳圖形中的信息。然而,大的圖形往往需要使用大量的T來(lái)獲取足夠的信息,這會(huì)限制這些模型的可擴(kuò)展性。為了解決這一問(wèn)題,我們可以使用依次掃描邊緣的模型(Parisotto等人于2016年提出),或許采取一些由粗到精的生成方法。
訓(xùn)練難度
我們發(fā)現(xiàn)訓(xùn)練這樣的圖形模型要比訓(xùn)練典型的長(zhǎng)短期記憶網(wǎng)絡(luò)模型更為困難,這些模型所要進(jìn)行訓(xùn)練的序列一般比較長(zhǎng),并且模型結(jié)構(gòu)不斷變化還會(huì)導(dǎo)致訓(xùn)練不穩(wěn)定。降低學(xué)習(xí)速率可以解決很多不穩(wěn)定問(wèn)題,但通過(guò)調(diào)整模型可以獲得更加令人滿(mǎn)意的解決方案。
本文中,我們提出了一個(gè)強(qiáng)大的深度生成模型,其能夠通過(guò)一個(gè)序列性過(guò)程生成任意形。我們?cè)谝恍﹫D形生成問(wèn)題中對(duì)它的屬性進(jìn)行了研究。這一模型已經(jīng)展現(xiàn)出很大的潛力,并且與標(biāo)準(zhǔn)LSTM模型相比具有獨(dú)特的優(yōu)勢(shì)。我們希望我們的研究成果能夠促進(jìn)這方面的進(jìn)一步研究,進(jìn)而獲得更好的圖形生成模型。
-
圖形
+關(guān)注
關(guān)注
0文章
71瀏覽量
19265 -
DeepMind
+關(guān)注
關(guān)注
0文章
129瀏覽量
10818
原文標(biāo)題:DeepMind提出圖形的「深度生成式模型」,可實(shí)現(xiàn)「任意」圖形的生成
文章出處:【微信號(hào):AItists,微信公眾號(hào):人工智能學(xué)家】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
利用對(duì)稱(chēng)性化簡(jiǎn)求解對(duì)稱(chēng)電路
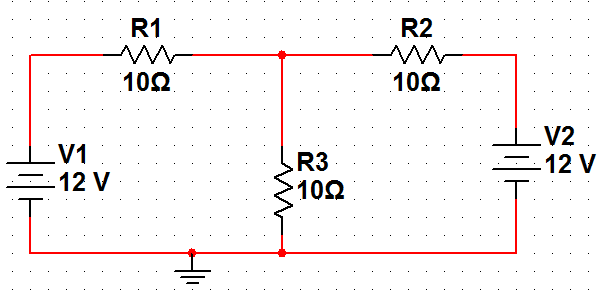
運(yùn)放的哪些參數(shù)可以反映出它的不對(duì)稱(chēng)性?
對(duì)稱(chēng)性加密算法
關(guān)于電源排序的解決方案你了解嗎
對(duì)稱(chēng)性對(duì)傅里葉系數(shù)的影響
基于幾何對(duì)稱(chēng)性的顱骨復(fù)原技術(shù)
對(duì)稱(chēng)性和格點(diǎn)理論在矩量法中的應(yīng)用
機(jī)械結(jié)構(gòu)對(duì)稱(chēng)性實(shí)例設(shè)計(jì)
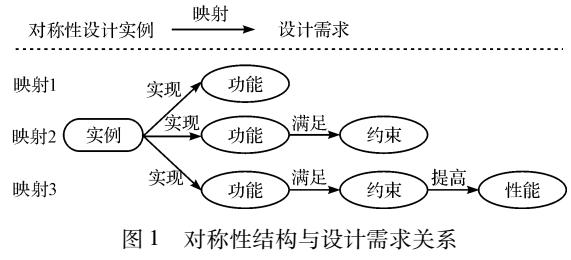
對(duì)稱(chēng)性對(duì)傅立葉系數(shù)的影響有哪些
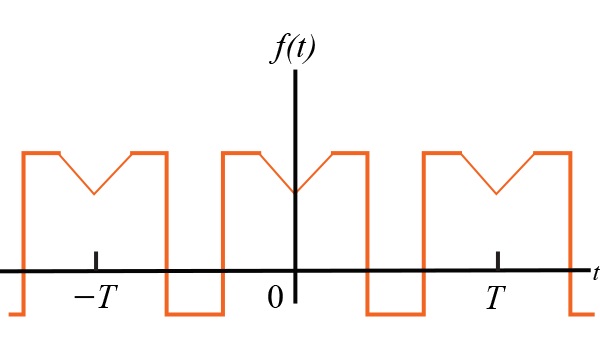
SHARC-Request評(píng)估碼的DTS對(duì)稱(chēng)性

信號(hào)的對(duì)稱(chēng)性如何簡(jiǎn)化計(jì)算傅里葉系數(shù)
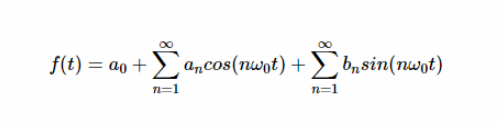




 如何在圖形生成過(guò)程中處理元素的對(duì)稱(chēng)性和排序,并提供可能的解決方案
如何在圖形生成過(guò)程中處理元素的對(duì)稱(chēng)性和排序,并提供可能的解決方案










評(píng)論