1.最小項的基本概念
由A、B、C三個邏輯變量構成的許多乘積項中有八個被稱為A、B、C的最小項的乘積項,它們的特點是
1.每項都只有三個因子
2.每個變量都是它的一個因子
3.每一變量或以原變量(A、B、C)的形式出現,或以反(非)變量(A、B、C)的形式出現,各出現一次
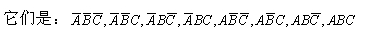
一般情況下,對n個變量來說,最小項共有2n個,如n=3時,最小項有23=8個
2.最小項的性質
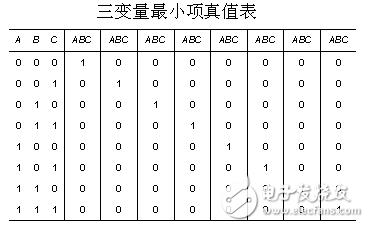
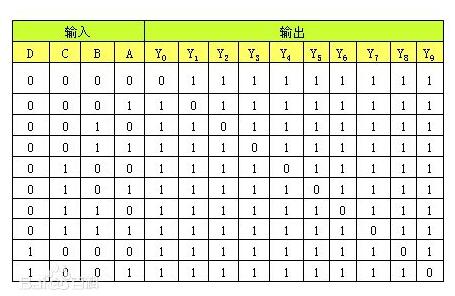
為了分析最小項的性質,以下列出3個變量的所有最小項的真值表。
由此可見,最小項具有下列性質:
(1)對于任意一個最小項,只有一組變量取值使得它的值為1,而在變量取其他各組值時,這個最小項的值都是0。
(2)不同的最小項,使它的值為1的那一組變量取值也不同。
(3)對于變量的任一組取值,任意兩個最小項的乘積為0。
(4)對于變量的任一組取值,全體最小項之和為1。
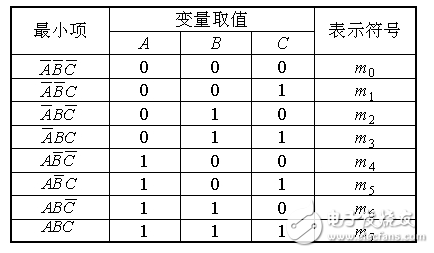
3.最小項的編號
最小項通常用mi表示,下標i即最小項編號,用十進制數表示。以ABC為例,因為它和011相對應,所以就稱ABC是和變量取值011相對應的最小項,而011相當于十進制中的3,所以把ABC記為m3按此原則,3個變量的最小項
二、邏輯函數的最小項表達式


三、用卡諾圖表示邏輯函數
1.卡諾圖的引出
一個邏輯函數的卡諾圖就是將此函數的最小項表達式中的各最小項相應地填入一個特定的方格圖內,此方格圖稱為卡諾圖。
卡諾圖是邏輯函數的一種圖形表示。
下面從討論一變量卡諾圖開始,逐步過渡到多變量卡諾圖。
大家知道,n個變量的邏輯函數有2n個最小項,因此一個變量的邏輯函數有兩個最小項。
比如有一個變量D,其邏輯函數L的最小項表達式為:
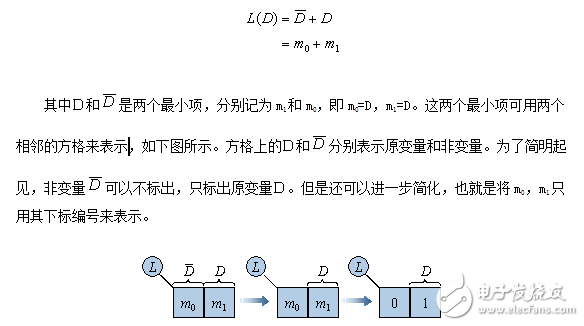
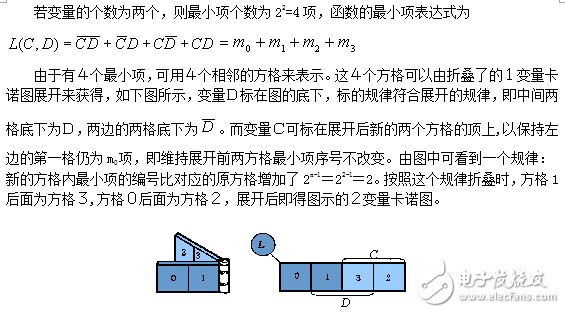
綜上所述,可歸納“折疊展開”的法則如下:
①新增加的方格按展開方向應標以新變量。
②新的方格內最小項編號應為展開前對應方格編號加2n-1。
按照同樣的方法,可從折疊的2變量卡諾圖展開獲得3變量卡諾圖。3變量邏輯函數L(B,C,D)應有8個最小項,可用8個相鄰的方格來表示。新增加的4個方格按展開方向應標以新增加的變量B(以區別于原來的變量C、D)。而且,新增加的方格內最小項的編號為展開前對應方格編號加2n-1=23-1=4,這樣即可獲得3變量卡諾圖如下:
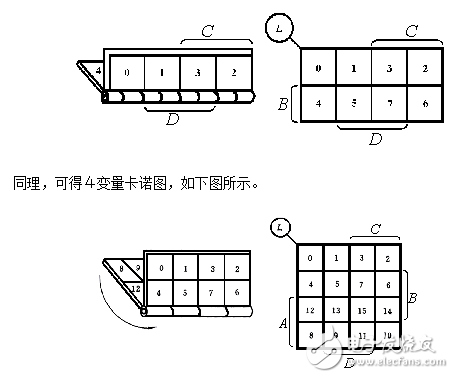
在使用時,只要熟悉了卡諾圖上各變量的取值情況(即方格外各變量A、B、C、D等取值的區域),就可直接填入對應的最小項。
將上圖中的數碼編號與最小項的編號——對應,可以得到下面這種形式的卡諾圖。
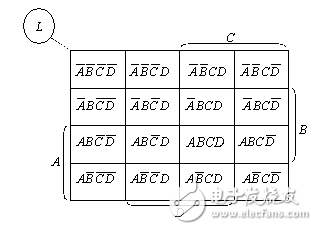
2.卡諾圖的特點
上面所得各種變量的卡諾圖,其共同特點是可以直接觀察相鄰項
。也就是說,各小方格對應于各變量不同的組合,而且上下左右在幾何上相鄰的方格內只有一個因子有差別,這個重要特點成為卡諾圖化簡邏輯函數的主要依據。在卡諾圖水平方向的同一行里,最左和最右端的方格也是符合上述相鄰規律的,例如,m4和m6的差別僅在C和。同樣,垂直方向同一列里最上端和最下端兩個方格也是相鄰的,這是因為都只有一個因子有差別。這個特點說明卡諾圖呈現循環鄰接的特性。
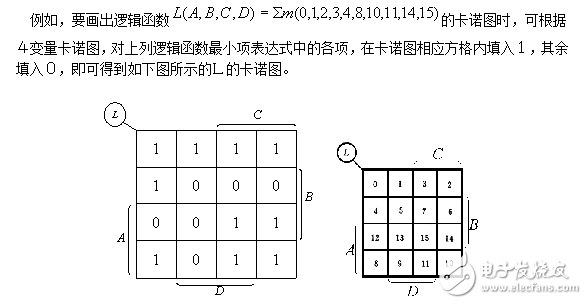
3.已知邏輯函數畫卡諾圖
根據邏輯函數的最小項表達式和卡諾圖的一般形式,就可以得到相應的卡諾圖。

-
真值表
+關注
關注
0文章
25瀏覽量
15162
發布評論請先 登錄
相關推薦
怎么利用QuartuesII查元件真值表
怎么利用QuartusII查元件真值表
求常用單片機的功能表、引腳圖、真值表
輸入真值表相同 輸出結果不同 74HC138
LUT真值表在實施期間發生了變化
門電路的計算方式 門電路工作原理真值計算
真值表,真值表是什么意思
怎么理解邏輯真值表_真值表如何推出邏輯表達式




 邏輯真值表怎么列出的_真值表是怎么畫出來的
邏輯真值表怎么列出的_真值表是怎么畫出來的












評論