如果我們有許多冗余的數(shù)據(jù),我們可能需要對特征量進行降維(Dimensionality Reduction)。
我們可以找到兩個非常相關(guān)的特征量,可視化,然后用一條新的直線來準(zhǔn)確的描述這兩個特征量。例如圖10-1所示,x1和x2是兩個單位不同本質(zhì)相同的特征量,我們可以對其降維。
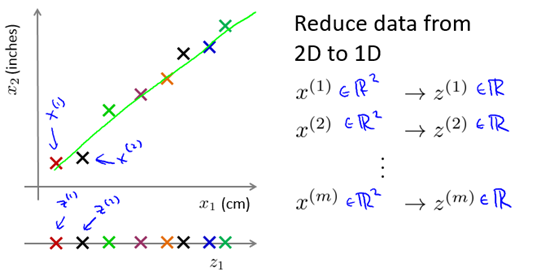
圖10-1 一個2維到1維的例子
又如圖10-2所示的3維到2維的例子,通過對x1,x2,x3的可視化,發(fā)現(xiàn)雖然樣本處于3維空間,但是他們大多數(shù)都分布在同一個平面中,所以我們可以通過投影,將3維降為2維。
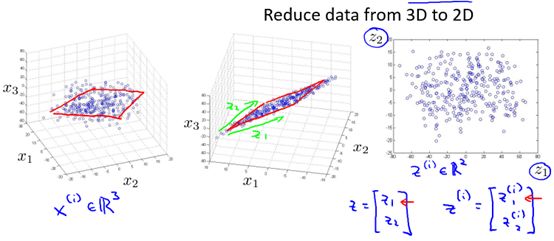
圖10-2 一個3維到2維的例子
降維的好處很明顯,它不僅可以數(shù)據(jù)減少對內(nèi)存的占用,而且還可以加快學(xué)習(xí)算法的執(zhí)行。
注意,降維只是減小特征量的個數(shù)(即n)而不是減小訓(xùn)練集的個數(shù)(即m)。
10.1.2 Motivation two: Visualization
我們可以知道,但特征量維數(shù)大于3時,我們幾乎不能對數(shù)據(jù)進行可視化。所以,有時為了對數(shù)據(jù)進行可視化,我們需要對其進行降維。我們可以找到2個或3個具有代表性的特征量,他們(大致)可以概括其他的特征量。
例如,描述一個國家有很多特征量,比如GDP,人均GDP,人均壽命,平均家庭收入等等。想要研究國家的經(jīng)濟情況并進行可視化,我們可以選出兩個具有代表性的特征量如GDP和人均GDP,然后對數(shù)據(jù)進行可視化。如圖10-3所示。
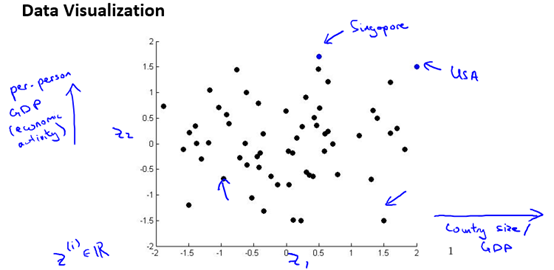
圖10-3 一個可視化的例子
10.2 Principal Component Analysis
主成分分析(Principal Component Analysis : PCA)是最常用的降維算法。
10.2.1 Problem formulation
首先我們思考如下問題,對于正交屬性空間(對2維空間即為直角坐標(biāo)系)中的樣本點,如何用一個超平面(直線/平面的高維推廣)對所有樣本進行恰當(dāng)?shù)谋磉_?
事實上,若存在這樣的超平面,那么它大概應(yīng)具有這樣的性質(zhì):
最近重構(gòu)性: 樣本點到這個超平面的距離都足夠近;
最大可分性:樣本點在這個超平面上的投影能盡可能分開。
下面我們以3維降到2維為例,來試著理解為什么需要這兩種性質(zhì)。圖10-4給出了樣本在3維空間的分布情況,其中圖(2)是圖(1)旋轉(zhuǎn)調(diào)整后的結(jié)果。在10.1節(jié)我們默認(rèn)以紅色線所畫平面(不妨稱之為平面s1)為2維平面進行投影(降維),投影結(jié)果為圖10-5的(1)所示,這樣似乎還不錯。那為什么不用藍(lán)色線所畫平面(不妨稱之為平面s2)進行投影呢? 可以想象,用s2投影的結(jié)果將如圖10-5的(2)所示。
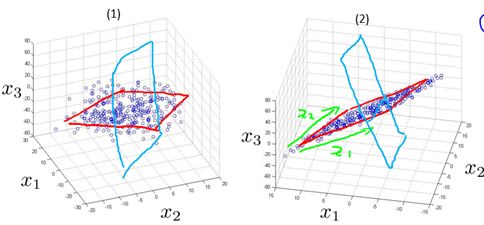
圖10-4 樣本在3維正交空間的分布
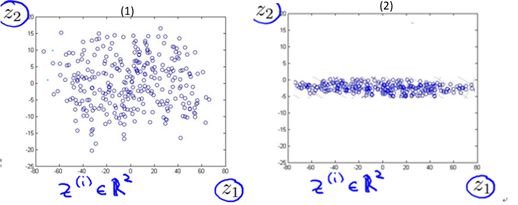
圖10-5 樣本投影在2維平面后的結(jié)果
由圖10-4可以很明顯的看出,對當(dāng)前樣本而言,s1平面比s2平面的最近重構(gòu)性要好(樣本離平面的距離更近);由圖10-5可以很明顯的看出,對當(dāng)前樣本而言,s1平面比s2平面的最大可分性要好(樣本點更分散)。不難理解,如果選擇s2平面進行投影降維,我們會丟失更多(相當(dāng)多)的特征量信息,因為它的投影結(jié)果甚至可以在轉(zhuǎn)化為1維。而在s1平面上的投影包含更多的信息(丟失的更少)。
這樣是否就是說我們從3維降到1維一定會丟失相當(dāng)多的信息呢? 其實也不一定,試想,如果平面s1投影結(jié)果和平面s2的類似,那么我們可以推斷這3個特征量本質(zhì)上的含義大致相同。所以即使直接從3維到1維也不會丟失較多的信息。這里也反映了我們需要知道如何選擇到底降到幾維會比較好(在10.2.3節(jié)中討論)。
讓我們高興的是,上面的例子也說明了最近重構(gòu)性和最大可分性可以同時滿足。更讓人興奮的是,分別以最近重構(gòu)性和最大可分性為目標(biāo),能夠得到PCA的兩種等價推導(dǎo)。
一般的,將特征量從n維降到k維:
以最近重構(gòu)性為目標(biāo),PCA的目標(biāo)是找到k個向量,將所有樣本投影到這k個向量構(gòu)成的超平面,使得投影的距離最小(或者說投影誤差projection error最小)。
以最大可分性為目標(biāo),PCA的目標(biāo)是找到k個向量,將所有樣本投影到這k個向量構(gòu)成的超平面,使得樣本點的投影能夠盡可能的分開,也就是使投影后的樣本點方差最大化。
注意: PCA和線性回歸是不同的,如圖10-6所示,線性回歸是以平方誤差和(SSE)最小為目標(biāo),參見1.2.4節(jié);而PCA是使投影(二維即垂直)距離最小;PCA與標(biāo)記或者預(yù)測值完全無關(guān),而線性回歸是為了預(yù)測y的值。
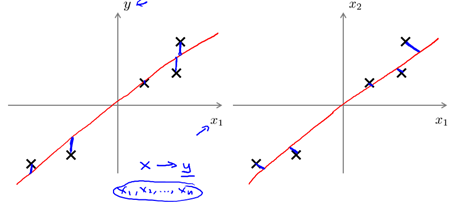
圖10-6 PCA不是線性回歸
分別基于上述兩種目標(biāo)的具體推導(dǎo)過程參見周志華老師的《機器學(xué)習(xí)》P230。從方差的角度推導(dǎo)參見李宏毅老師《機器學(xué)習(xí)》課程Unsupervised Learning: Principle Component Analysis(http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2017/Lecture/PCA.mp4)。
兩種等價的推導(dǎo)結(jié)論是:對協(xié)方差矩陣進行特征值分解,將求得的特征值進行降序排序,再取前k個特征值對應(yīng)的特征向量構(gòu)成。
其中
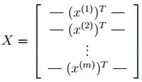
10.2.2 Principal Component Analysis Algorithm
基于上一節(jié)給出的結(jié)論,下面給出PCA算法。
輸入:訓(xùn)練集: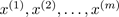
過程:
數(shù)據(jù)預(yù)處理:對所有樣本進行中心化(即使得樣本和為0)
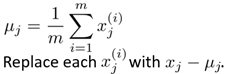
計算樣本的協(xié)方差矩陣(Sigma)
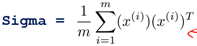
在matlab中具體實現(xiàn)如下,其中X為m*n的矩陣:
Sigma = (1/m) * X'* X;
對2中求得的協(xié)方差矩陣Sigma進行特征值分解
在實踐中通常對協(xié)方差矩陣進行奇異值分解代替特征值分解。在matlab中實現(xiàn)如下:
[U, S, V] = svd(Sigma); (svd即為matlab中奇異值分解的內(nèi)置函數(shù))
取最大的k個特征值所對應(yīng)的特征向量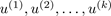
在matlab具體實現(xiàn)時,Ureduce =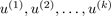
經(jīng)過了上述4步得到了投影矩陣Ureduce,利用Ureduce就可以得到投影后的樣本值
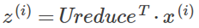
下面總結(jié)在matlab中實現(xiàn)PCA的全部算法(假設(shè)數(shù)據(jù)已被中心化)
Sigma = (1/m) * X' * X; % compute the covariance matrix
[U,S,V] = svd(Sigma); % compute our projected directions
Ureduce = U(:,1:k); % take the first k directions
Z = Ureduce' * X; % compute the projected data points
10.2.3 Choosing the Number of Principal Components
如何選擇k(又稱為主成分的個數(shù))的值?
首先,試想我們可以使用PCA來壓縮數(shù)據(jù),我們應(yīng)該如何解壓?或者說如何回到原本的樣本值?事實上我們可以利用下列等式計算出原始數(shù)據(jù)的近似值Xapprox:
Xapprox = Z * Ureduce (m*n = m*k * k*n )
自然的,還原的數(shù)據(jù)Xapprox越接近原始數(shù)據(jù)X說明PCA誤差越小,基于這點,下面給出選擇k的一種方法:

結(jié)合PCA算法,選擇K的算法總結(jié)如下:

這個算法效率特別低。在實際應(yīng)用中,我們只需利用svd()函數(shù),如下:

10.2.4 Advice for Applying PCA
PCA通常用來加快監(jiān)督學(xué)習(xí)算法。
PCA應(yīng)該只是通過訓(xùn)練集的特征量來獲取投影矩陣Ureduce,而不是交叉檢驗集或測試集。但是獲取到Ureduce之后可以應(yīng)用在交叉檢驗集和測試集。
避免使用PCA來防止過擬合,PCA只是對特征量X進行降維,并沒有考慮Y的值;正則化是防止過擬合的有效方法。
不應(yīng)該在項目一開始就使用PCA: 花大量時間來選擇k值,很可能當(dāng)前項目并不需要使用PCA來降維。同時,PCA將特征量從n維降到k維,一定會丟失一些信息。
僅僅在我們需要用PCA的時候使用PCA: 降維丟失的信息可能在一定程度上是噪聲,使用PCA可以起到一定的去噪效果。
PCA通常用來壓縮數(shù)據(jù)以加快算法,減少內(nèi)存使用或磁盤占用,或者用于可視化(k=2, 3)。
-
算法
+關(guān)注
關(guān)注
23文章
4601瀏覽量
92673 -
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8382瀏覽量
132444
原文標(biāo)題:Stanford機器學(xué)習(xí)筆記-10. 降維(Dimensionality Reduction)
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
常用python機器學(xué)習(xí)庫盤點
基于Autoencoder網(wǎng)絡(luò)的數(shù)據(jù)降維和重構(gòu)
基于雜波協(xié)方差矩陣特征向量分析STAP降維方法
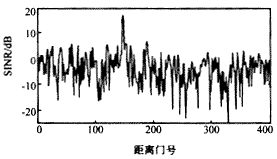
基于譜特征嵌入的腦網(wǎng)絡(luò)狀態(tài)觀測矩陣降維方法
想掌握機器學(xué)習(xí)技術(shù)?從了解特征工程開始
如何使用自適應(yīng)嵌入的半監(jiān)督多視角特征實現(xiàn)降維的方法概述
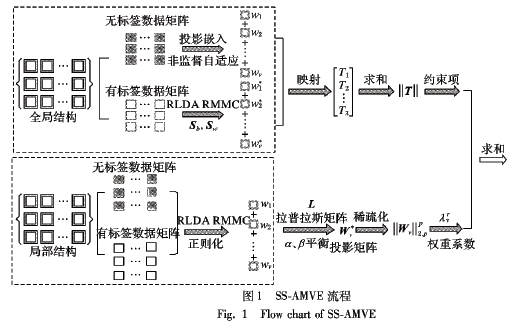
機器學(xué)習(xí)算法都有哪一些
機器學(xué)習(xí)之特征提取 VS 特征選擇

如何使用FPGA實現(xiàn)高光譜圖像奇異值分解降維技術(shù)
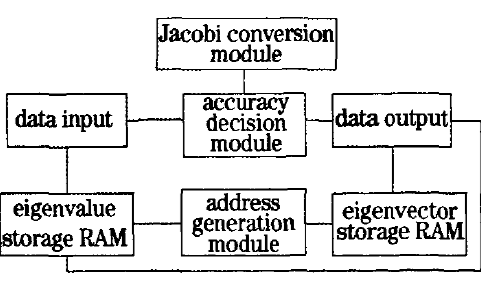
基于最大信息系數(shù)與冗余分?jǐn)偛呗缘?b class='flag-5'>特征選擇方法

一種基于嵌入式特征提取的多標(biāo)記分類算法
一種新型的數(shù)據(jù)采集多視圖降維算法技術(shù)
特征選擇和機器學(xué)習(xí)的軟件缺陷跟蹤系統(tǒng)對比
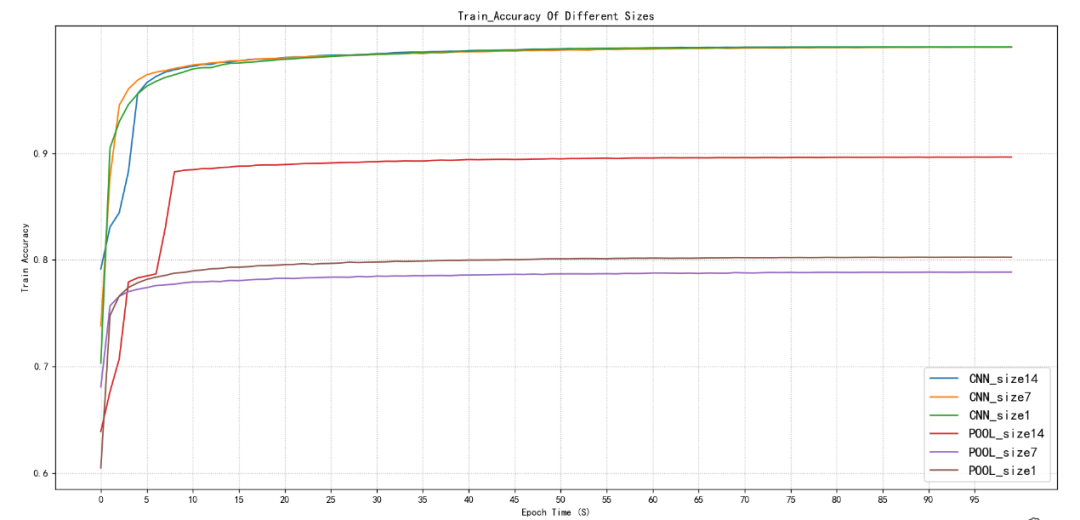
淺析卷積降維與池化降維的對比




 機器學(xué)習(xí)筆記:冗余的數(shù)據(jù)對特征量進行降維
機器學(xué)習(xí)筆記:冗余的數(shù)據(jù)對特征量進行降維










評論