RF采樣轉換器可捕獲高頻信號和大帶寬信號；但是，并非每種應用都能利用需要極高速采樣的信號。就帶寬或輸出頻率不過高的情況而言，利用RF采樣轉換器的高采樣速率能力仍存在一大優勢。采樣定理規定，采樣速率必須至少是信號最大帶寬的兩倍。低于該速率的采樣被稱為欠采樣，會引起混疊現象。高于該速率的采樣被稱為過采樣。過采樣可提供一些看似能讓您無視物理學定律的處理優勢。模數轉換器（ADC）的關鍵測量參數之一是信噪比（SNR）。SNR可衡量所需信號功率與第一奈奎斯特區內全部噪聲功率之間的相對電平。該奈奎斯特區的帶寬等于采樣速率除以2（Fs/2）。要記得，所有信號和噪聲均會折返到第一奈奎斯特區。該區實際上代表了該器件的整個帶寬。過采樣的一大好處是，圖像分量可在頻率空間里被進一步分離。這允許更輕松的模擬濾波，以便消除能向下混疊到被捕獲的帶寬范圍內并降低接收器靈敏度的干擾信號。圖1展示了兩個實例：一種以接近奈奎斯特速率的速率采樣的信號以及一種被過采樣的信號。在被過采樣的實例中，模擬抗混疊濾波器更易實現。

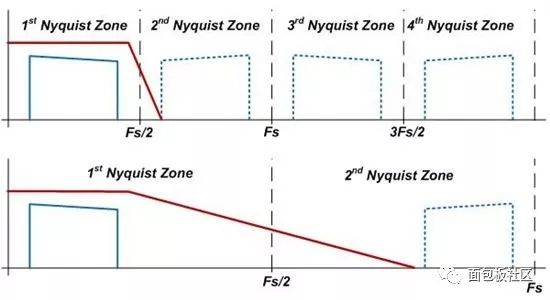
圖1：濾波器對奈奎斯特速率采樣與過采樣的影響過采樣可不受理論量化噪聲限制來改善該器件的SNR性能。這種量化噪聲跨奈奎斯特帶寬均勻分布。通過提高采樣速率，同樣的量化噪聲被分散在更大的奈奎斯特帶寬范圍內。所需的信號保持不變。抽取與數字濾波相結合可降低噪聲帶寬，卻不會對所需的信號造成影響。注意，抽取意味著過采樣，因為必須有可供移除的其它樣本。在RF采樣ADC中，更常提及的是抽取因子，而非過采樣速率；但這些參數實際上是等效的。例如，要使抽取因子為2，必須讓信號的過采樣因子至少為2。在這個例子中，信號功率保持不變，但奈奎斯特帶寬被減半。這就消除了一半的噪聲功率，從而讓該ADC的SNR增加了3dB。第一個方程式表示因量化噪聲得到的理想SNR，其中N是該轉換器的位數。第二個方程式則表示與抽取因子D相關的SNR改善值。

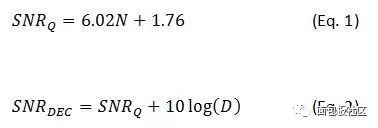
根據純量化噪聲分析，采樣速率每提高三倍（即增至原來的四倍），可讓分辨率增加一個有效位。從理論上講，通過以16倍于最小奈奎斯特速率的速率采樣，12位數據轉換器可實現14位轉換器的SNR性能。

在實踐中，由于和孔徑抖動、時鐘抖動及熱噪聲相關的其它損害，RF采樣數據轉換器無法實現與量化噪聲限值相當的SNR性能；但是，過采樣技術仍能提供幾乎完全一樣的相關SNR改善值。在許多通信系統中，這一好處是至關重要的。