在現代密碼學的加密方法中會用到大量隨機的、不可預知的數字來確保數據與信息的安全性。因此，可靠的隨機數發生器對加密系統至關重要。科學家一直在不斷嘗試構建更好的隨機數發生器，而面臨的一個重大挑戰就在于——我們很難判斷發生器輸出的隨機數是否真的不可預測。

之所以說每天被使用數千億次來加密電子網絡中的數據的隨機數字并非絕對隨機，是因為它們都是由軟件公式或物理設備產生的，“隨機”輸出會受到設備本身的缺陷、元件的老化、意外故障或對手的篡改等因素的影響，使隨機數發生器偏離其預期設計，導致未被發現的偏差。雖然可以通過一些統計測試來進行檢查，但是單單對輸出進行統計測試并不能確保輸出就是不可預測的，尤其是對于出現設備被對手篡改的情況。

也就是說，輸出生成的內部運作是未知的。例如，有些被稱為偽隨機序列發生器的算術運算能產生完全可預測的數字序列；但是這些序列也并沒有任何可識別的規律，因此對從不知道這些數字是如何產生的人來說，很難將這些由偽隨機過程產生的數字序列與通過真正隨機方法獲得的序列區分開來。

這也就是為什么，在幾年前，美國國家標準與技術研究院（NIST）的物理學家 Peter Bierhorst 的團隊決定開發一種完全隨機的數字發生器。在密碼學領域，這意味著數字的完全“無法預測性”。而什么是真正的隨機？是量子力學。

Bierhorst’s 等人利用以量子物理學和狹義相對論發展出的隨機數發生器，實現了前所未有的安全性。他們將實驗細節發表在4月12日的《自然》雜志上，實驗中所用到的技術在確保隨機數的不可預測性上超越了之前的所有方法。

新的方法使用光子來產生數字位（定向于某一方向的光子為1，而另一方向的光子為0），這一實驗確切地見證了“鬼魅般的超距作用”。在實驗中，研究人員處理這些“鬼魅般”的輸出以驗證和量化數據中可用的隨機性，并生成一串更隨機的數位。

實驗原型系統所用到的激光器、反射鏡和透鏡分別被安置在三個不同的實驗室，其中兩個測量站位于一個L形建筑的兩端。整個設備被長約263米的光纖串聯在一起。Bierhorst 說：“一個經典信息源是否真的不可預測是很難被保證的，但量子信息源和協議就像是一個安全防護。我們確信沒有人能預測我們的數字。”

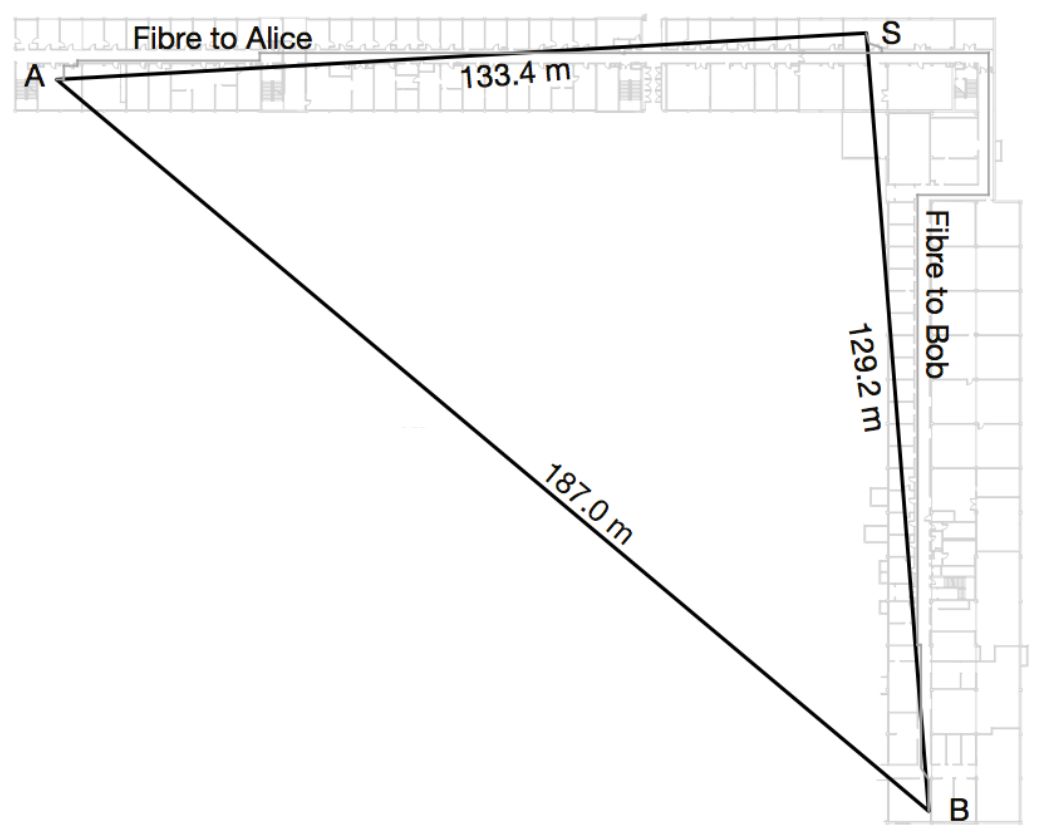
○來源（S）、測量站（A）和（B）分別所在的三個實驗室的相對位置：每次試驗中，源所在的實驗室會產生一對非極化的糾纏態光子，分別被送往實驗室A和B進行測量。| 圖片來源：Bierhorst et. al.

Bierhorst 解釋說：“拋擲硬幣可能看起來像是一個隨機過程，但是一旦能看到硬幣的確切路徑，就可以預測它的結果。而量子隨機性則是真正的隨機，我們之所以能看到量子隨機性，是因為只有量子系統能產生測量選擇和結果之間的統計相關性。”

這是因為即使你能通過準備一個有著完全相同的初始狀態的量子粒子來重復一次量子實驗，對它在完全相同的條件下進行測量，仍有可能得到完全不同的結果。這與拋擲硬幣不同——因為當拋擲硬幣時，拇指的力量、風的方向都是可在落地之前決定結果的初始條件。而“拋擲”一個微小的量子粒子的結果只有在它“落地”的那一刻才會以概率形式存在。因此，電子、光子和原子確實都是隨機的。

量子力學提供了一種優質的隨機性來源，因為一些量子粒子（同時存在0和1的“疊加”）的測量具有根本不可預知的結果。研究人員可以輕易地測量量子系統，但卻很難證明測量是由量子系統形成，而非經典系統偽裝的。

在NIST的實驗中，研究人員在關閉了或許能導致非隨機數位看起來“隨機”的漏洞時，對光子對之間奇異的量子相關性進行了觀測。實驗的運作原理是：研究人員會先在糾纏態下準備兩個光子，然后再將每個光子發送到不同的遠程測量站，并記錄下光子在測量站的偏振。在測量過程中，由于兩個測量站相距太遠，因此光子無法相互作用，除非信號的傳播速度比光速還快。然而因為光子的糾纏性質，得到的測量結果是強相關的。這種相關性可以通過被稱為違反貝爾不等式的統計標準來檢測的。

而兩個相距甚遠的光子間的強烈相關行為表明，它們可以被用來設計成超光速的通信設備。而這的確是有可能的，除非光子的測量結果完全不可預測，因為這種情況會導致混亂且難以破譯的消息，任何在通信設備中使用這種光子的嘗試都將失敗。但由于比光速更快的通信是不可能的，因此違反貝爾不等式就意味著隨機測量輸出。也就是說，這種違反提供了隨機性的實驗性標志。

其實，科學家已經在許多實驗中觀察到貝爾不等式的違反，并且一直知曉它們與隨機性之間的關系。但量子信息研究人員開始開發能利用這種連接的工具僅是近幾年才開始的。

貝爾測試中的一個關鍵難點在于，大多數違反貝爾不等式的實驗都會受到漏洞的影響，這意味著它們不能被視為黑盒示范。在過去幾年中，無漏洞實驗雖然已經得以開展，但它們仍存在很大的技術挑戰。特別是，在這些實驗中觀察到的貝爾不等式的違反幅度雖然足以證實光子的相關行為，但是卻因為太低而不足以驗證用于密碼學目的的隨機性的存在。

Bierhorst 等人改進了已有的無漏洞實驗裝置，讓實現這種隨機性成為可能。但是這一閾值幾乎很難達到。每次在實驗中測量一個光子時，所產生的隨機性（用0和1代表的比特）相當于投擲一枚著正面著地的概率為99.98%的硬幣。

通過很多次的運行，測量結果的序列應該能積累足夠大的不確定性，而讓真正隨機的比特能通過巧妙的后期處理得到“提取”。但是，現有的分析這些序列的方法不足以達到這個目標。因此， Bierhorst 和他的團隊針對觀測到的弱貝爾不等式違反，發展出了一套強大的統計技術：他們可以在大約10分鐘的數據采集中生成1024個隨機位，相當于對5千5百萬個光子對進行了測量。

Bierhorst說：“完美的硬幣投擲是均衡的，我們制作了1024個幾乎完全均衡的比特，每一個為0或1的概率都非常接近。”其他研究人員以前使用貝爾測試來生成隨機數，但NIST方法是第一個使用無漏洞貝爾測試并通過提取來處理結果數據的方法。

對 Bierhorst 來說，通過量子力學發展出的隨機數發生器不僅是一個實用的工具，他所進行的測試進一步證明量子粒子真的存在奇異的概率，并且不能被預先確定。知道宇宙真的存在這種隨機性是件令人欣喜的事。而現在，我們或許就可以利用這種隨機性來強化數字時代的信息安全。