微軟研究人員在ICLR 2018發(fā)表了一種新的GAN(對抗網(wǎng)絡(luò)生成)訓(xùn)練方法,boundary-seeking GAN(BGAN),可基于離散值訓(xùn)練GAN,并提高了GAN訓(xùn)練的穩(wěn)定性。
對抗生成網(wǎng)絡(luò)
首先,讓我們溫習(xí)一下GAN(對抗生成網(wǎng)絡(luò))的概念。簡單來說,GAN是要生成“以假亂真”的樣本。這個(gè)“以假亂真”,用形式化的語言來說,就是假定我們有一個(gè)模型G(生成網(wǎng)絡(luò)),該模型的參數(shù)為θ,我們要找到最優(yōu)的參數(shù)θ,使得模型G生成的樣本的概率分布Qθ與真實(shí)數(shù)據(jù)的概率分布P盡可能接近。即:
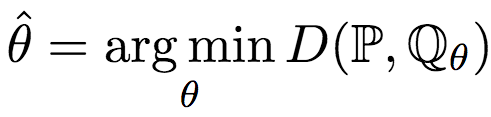
其中,D(P, Qθ)為P與Qθ差異的測度。
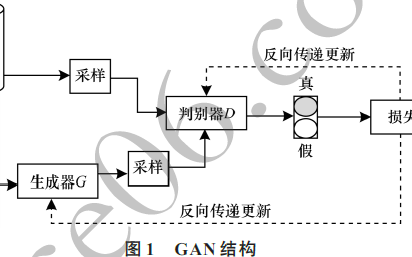
GAN的主要思路,是通過引入另一個(gè)模型D(判別網(wǎng)絡(luò)),該模型的參數(shù)為φ,然后定義一個(gè)價(jià)值函數(shù)(value function),找到最優(yōu)的參數(shù)φ,最大化這一價(jià)值函數(shù)。比如,最初的GAN(由Goodfellow等人在2014年提出),定義的價(jià)值函數(shù)為:
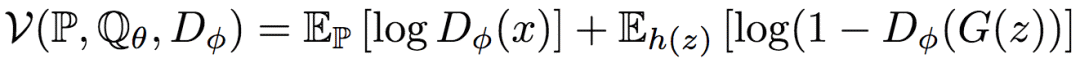
其中,Dφ為一個(gè)使用sigmoid激活輸出的神經(jīng)網(wǎng)絡(luò),也就是一個(gè)二元分類器。價(jià)值函數(shù)的第一項(xiàng)對應(yīng)真實(shí)樣本,第二項(xiàng)對應(yīng)生成樣本。根據(jù)公式,D將越多的真實(shí)樣本歸類為真(1),同時(shí)將越多的生成樣本歸類為假(0),D的價(jià)值函數(shù)的值就越高。
GAN的精髓就在于讓生成網(wǎng)絡(luò)G和判別網(wǎng)絡(luò)D彼此對抗,在對抗中提升各自的水平。形式化地說,GAN求解以下優(yōu)化問題:
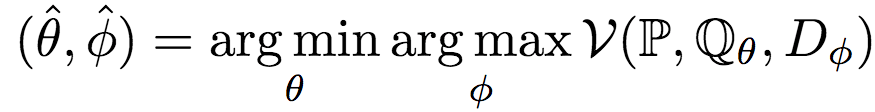
如果你熟悉Jensen-Shannon散度的話,你也許已經(jīng)發(fā)現(xiàn)了,之前提到的最初的GAN的價(jià)值函數(shù)就是一個(gè)經(jīng)過拉伸和平移的Jensen-Shannon散度:2 * DJSD(P||Qθ) - log 4. 除了這一Jensen-Shannon散度的變形外,我們還可以使用其他測度衡量分布間的距離,Nowozin等人在2016年提出的f-GAN,就將GAN的概念推廣至所有f-散度,例如:
Jensen-Shannon
Kullback–Leibler
Pearson χ2
平方Hellinger
當(dāng)然,實(shí)際訓(xùn)練GAN時(shí),由于直接計(jì)算這些f-散度比較困難,往往采用近似的方法計(jì)算。
GAN的缺陷
GAN有兩大著名的缺陷:難以處理離散數(shù)據(jù),難以訓(xùn)練。
GAN難以處理離散數(shù)據(jù)
為了基于反向傳播和隨機(jī)梯度下降之類的方法訓(xùn)練網(wǎng)絡(luò),GAN要求價(jià)值函數(shù)在生成網(wǎng)絡(luò)的參數(shù)θ上完全可微。這使得GAN難以生成離散數(shù)據(jù)。
假設(shè)一下,我們給生成網(wǎng)絡(luò)加上一個(gè)階躍函數(shù)(step function),使其輸出離散值。這個(gè)階躍函數(shù)的梯度幾乎處處為0,這就使GAN無法訓(xùn)練了。
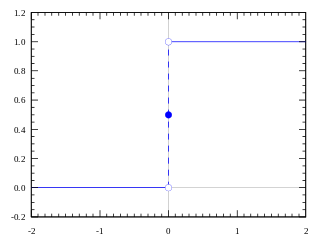
GAN難以訓(xùn)練
從直覺上說,訓(xùn)練判別網(wǎng)絡(luò)比訓(xùn)練生成網(wǎng)絡(luò)要容易得多,因?yàn)樽R(shí)別真假樣本通常比偽造真實(shí)樣本容易。所以,一旦判別網(wǎng)絡(luò)訓(xùn)練過頭了,能力過強(qiáng),生成網(wǎng)絡(luò)再怎么努力,也無法提高,換句話說,梯度消失了。
另一方面,如果判別網(wǎng)絡(luò)能力太差,胡亂分辨真假,甚至把真的誤認(rèn)為假的,假的誤認(rèn)為真的,那生成網(wǎng)絡(luò)就會(huì)很不穩(wěn)定,會(huì)努力學(xué)習(xí)讓生成的樣本更假——因?yàn)槿踔堑呐袆e網(wǎng)絡(luò)會(huì)把某些假樣本當(dāng)成真樣本,卻把另一些真樣本當(dāng)成假樣本。
還有一個(gè)問題,如果生成網(wǎng)絡(luò)湊巧在生成某類真樣本上特別得心應(yīng)手,或者,判別網(wǎng)絡(luò)對某類樣本的辨別能力相對較差,那么生成網(wǎng)絡(luò)會(huì)揚(yáng)長避短,盡量多生成這類樣本,以增大騙過判別網(wǎng)絡(luò)的概率,這就導(dǎo)致了生成樣本的多樣性不足。
所以,判別網(wǎng)絡(luò)需要訓(xùn)練得恰到好處才可以,這個(gè)火候非常難以控制。
強(qiáng)化學(xué)習(xí)和BGAN
那么,該如何避免GAN的缺陷呢?
我們先考慮離散值的情況。之所以GAN不支持生成離散值,是因?yàn)樯呻x散值導(dǎo)致價(jià)值函數(shù)(也就是GAN優(yōu)化的目標(biāo))不再處處可微了。那么,如果我們能對GAN的目標(biāo)做一些手腳,使得它既處處可微,又能衡量離散生成值的質(zhì)量,是不是可以讓GAN支持離散值呢?
關(guān)鍵在于,我們應(yīng)該做什么樣的改動(dòng)?關(guān)于這個(gè)問題,可以從強(qiáng)化學(xué)習(xí)中得到靈感。實(shí)際上,GAN和強(qiáng)化學(xué)習(xí)很像,生成網(wǎng)絡(luò)類似強(qiáng)化學(xué)習(xí)中的智能體,而騙過判別網(wǎng)絡(luò)類似強(qiáng)化學(xué)習(xí)中的獎(jiǎng)勵(lì),價(jià)值函數(shù)則是強(qiáng)化學(xué)習(xí)中也有的概念。而強(qiáng)化學(xué)習(xí)除了可以根據(jù)價(jià)值函數(shù)進(jìn)行外,還可以根據(jù)策略梯度(policy gradient)進(jìn)行。根據(jù)價(jià)值函數(shù)進(jìn)行學(xué)習(xí)時(shí),基于價(jià)值函數(shù)的值調(diào)整策略,迭代計(jì)算價(jià)值函數(shù),價(jià)值函數(shù)最優(yōu),意味著當(dāng)前策略是最優(yōu)的。而根據(jù)策略梯度進(jìn)行時(shí),直接學(xué)習(xí)策略,通過迭代計(jì)算策略梯度,調(diào)整策略,取得最大期望回報(bào)。
咦?這個(gè)策略梯度看起來很不錯(cuò)呀。引入策略梯度解決了離散值導(dǎo)致價(jià)值函數(shù)不是處處可微的問題。更妙的是,在強(qiáng)化學(xué)習(xí)中,基于策略梯度學(xué)習(xí),有時(shí)能取得比基于值函數(shù)學(xué)習(xí)更穩(wěn)定、更好的效果。類似地,引入策略梯度后GAN不再直接根據(jù)是否騙過判別網(wǎng)絡(luò)調(diào)整生成網(wǎng)絡(luò),而是間接基于判別網(wǎng)絡(luò)的評價(jià)計(jì)算目標(biāo),可以提高訓(xùn)練的穩(wěn)定度。
BGAN(boundary-seeking GAN)的思路正是如此。
BGAN論文的作者首先證明了目標(biāo)密度函數(shù)p(x)等于(?f/?T)(T(x))qθ(x)。其中,f為生成f-散度的函數(shù),f*為f的凸共軛函數(shù)。
令w(x) = (?f/?T)(T*(x)),則上式可以改寫為:
p(x) = (w*(x))qθ(x)
這樣改寫后,很明顯了,這可以看成一個(gè)重要性采樣(importance sampling)問題。(重要性采樣是強(qiáng)化學(xué)習(xí)中推導(dǎo)策略梯度的常用方法。)相應(yīng)地,w*(x)為最優(yōu)重要性權(quán)重(importance weight)。
類似地,令w(x) = (?f*/?T)(T(x)),我們可以得到f-散度的重要性權(quán)重估計(jì):
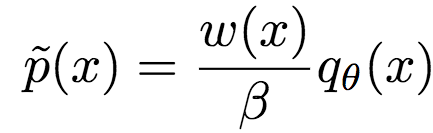
其中,β為分區(qū)函數(shù):
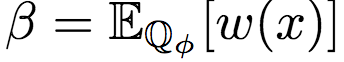
使用重要性權(quán)重作為獎(jiǎng)勵(lì)信號,可以得到基于KL散度的策略梯度:
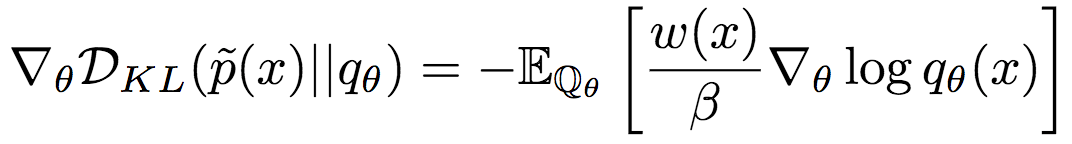
然而,由于這一策略梯度需要估計(jì)分區(qū)函數(shù)β(比如,使用蒙特卡洛法),因此,方差通常會(huì)比較大。因此,論文作者基于歸一化的重要性權(quán)重降低了方差。
令
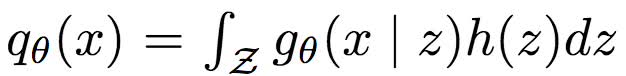
其中,gθ(x | z): Z -> [0, 1]d為條件密度,h(z)為z的先驗(yàn)。
令分區(qū)函數(shù)
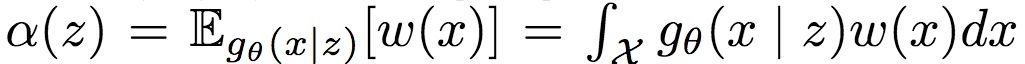
則歸一化的條件權(quán)重可定義為
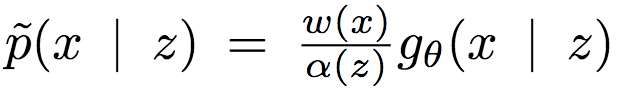
由此,可以得到期望條件KL散度:
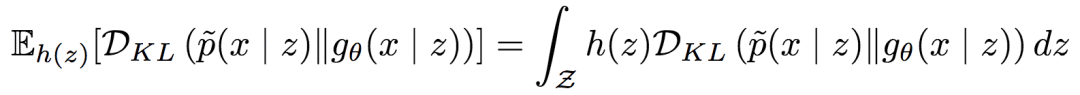
令x(m)~ gθ(x | z)為取自先驗(yàn)的樣本,又令
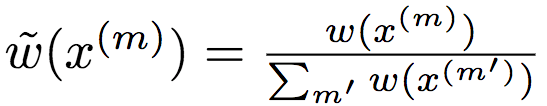
為使用蒙特卡洛估計(jì)的歸一化重要性權(quán)重,則期望條件KL散度的梯度為:
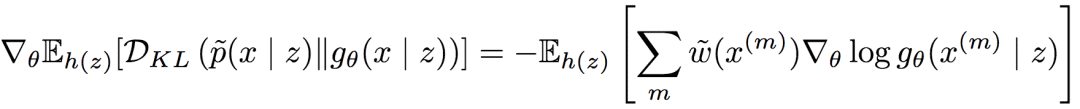
如此,論文作者成功降低了梯度的方差。
此外,如果考慮逆KL散度的梯度,則我們有:
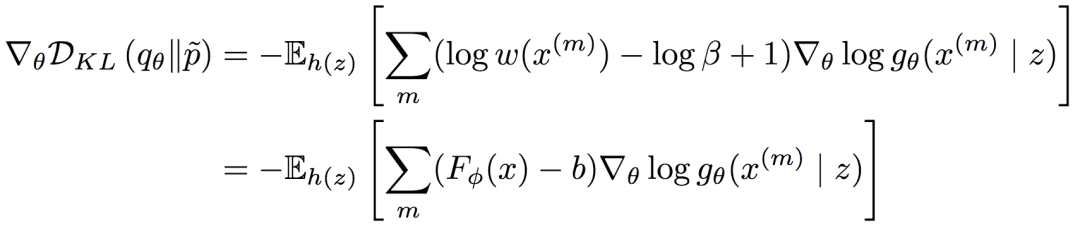
上式中,靜態(tài)網(wǎng)絡(luò)的輸出Fφ(x)可以視為獎(jiǎng)勵(lì)(reward),b可以視為基線(baseline)。因此,論文作者將其稱為基于強(qiáng)化的BGAN。
試驗(yàn)
離散
為了驗(yàn)證BGAN在離散設(shè)定下的表現(xiàn),論文作者首先試驗(yàn)了在CIFAR-10上訓(xùn)練一個(gè)分類器。結(jié)果表明,搭配不同f-散度的基于重要性取樣、強(qiáng)化的BGAN均取得了接近基線(交叉熵)的表現(xiàn),大大超越了WGAN(權(quán)重裁剪)的表現(xiàn)。
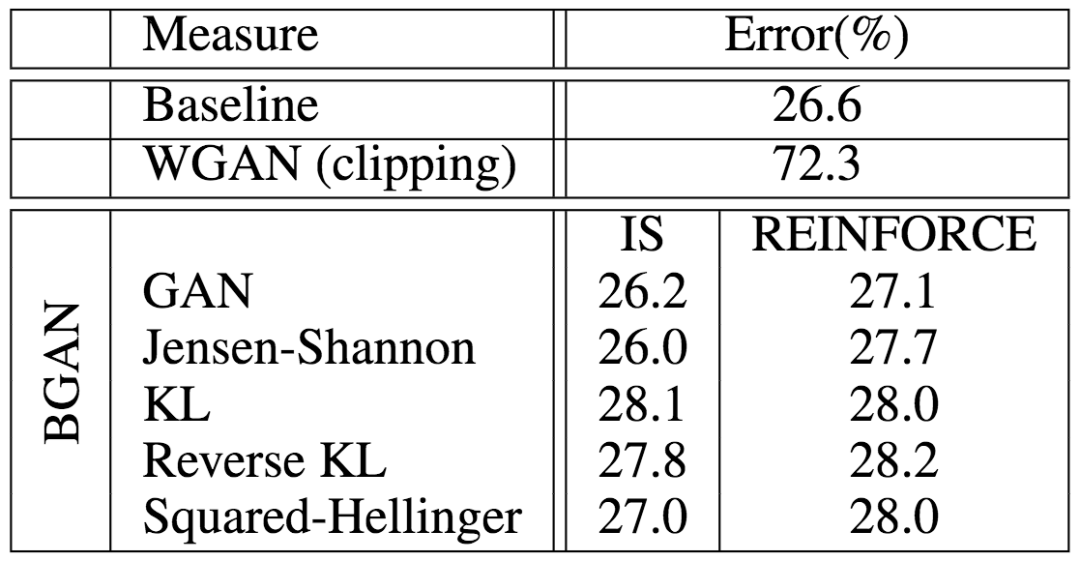
在MNIST上的試驗(yàn)表明,BGAN可以生成穩(wěn)定、逼真的手寫數(shù)字:
在MNIST上與WGAN-GP(梯度懲罰)的比較顯示,采用多種距離衡量,包括Wasserstein距離,BGAN都取得了更優(yōu)的表現(xiàn):
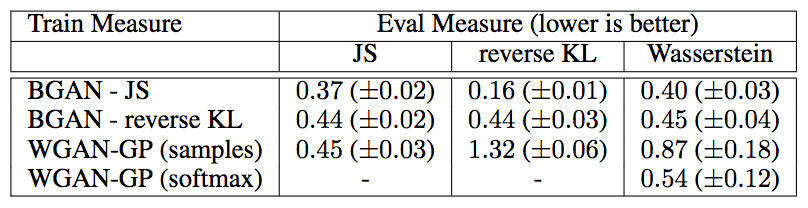
在quantized版本的CelebA數(shù)據(jù)集上的表現(xiàn):
左為降采樣至32x32的原圖,右為BGAN生成的圖片
下為隨機(jī)選取的在1-billion word數(shù)據(jù)集上訓(xùn)練的BGAN上生成的文本的3個(gè)樣本:

雖然這個(gè)效果還比不上當(dāng)前最先進(jìn)的基于RNN的模型,但此前尚無基于GAN訓(xùn)練離散值的模型能實(shí)現(xiàn)如此效果。
連續(xù)
論文作者試驗(yàn)了BGAN在CelebA、ImageNet、LSUN數(shù)據(jù)集上的表現(xiàn),均能生成逼真的圖像:
在CIFAR-10與原始GAN、使用代理損失(proxy loss)的DCGAN的比較表明,BGAN的表現(xiàn)和訓(xùn)練穩(wěn)定性都是最優(yōu)的:
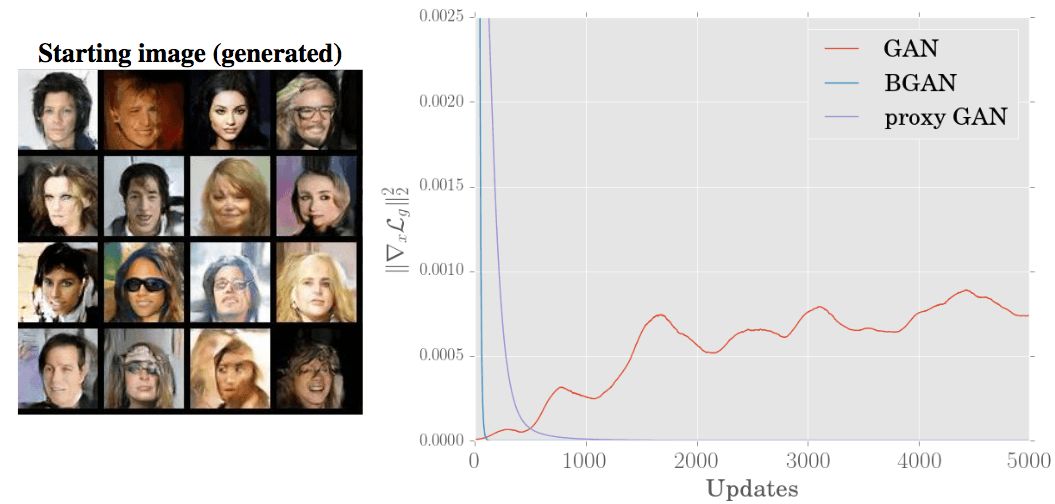
-
網(wǎng)絡(luò)
+關(guān)注
關(guān)注
14文章
7514瀏覽量
88627 -
GaN
+關(guān)注
關(guān)注
19文章
1918瀏覽量
72980 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4304瀏覽量
62429
原文標(biāo)題:BGAN:支持離散值、提升訓(xùn)練穩(wěn)定性的新GAN訓(xùn)練方法
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
圖像生成對抗生成網(wǎng)絡(luò)gan_GAN生成汽車圖像 精選資料推薦
一種基于機(jī)器學(xué)習(xí)的建筑物分割掩模自動(dòng)正則化和多邊形化方法
優(yōu)化神經(jīng)網(wǎng)絡(luò)訓(xùn)練方法有哪些?
研究人員提出一種基于哈希的二值網(wǎng)絡(luò)訓(xùn)練方法 比當(dāng)前方法的精度提高了3%
如何使用雙鑒別網(wǎng)絡(luò)進(jìn)行生成對抗網(wǎng)絡(luò)圖像修復(fù)方法的說明
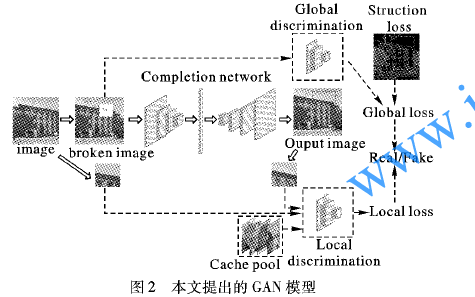
必讀!生成對抗網(wǎng)絡(luò)GAN論文TOP 10
生成對抗網(wǎng)絡(luò)GAN論文TOP 10,幫助你理解最先進(jìn)技術(shù)的基礎(chǔ)
一種利用生成式對抗網(wǎng)絡(luò)的超分辨率重建算法
一種側(cè)重于學(xué)習(xí)情感特征的預(yù)訓(xùn)練方法





 一種新的GAN(對抗網(wǎng)絡(luò)生成)訓(xùn)練方法
一種新的GAN(對抗網(wǎng)絡(luò)生成)訓(xùn)練方法











評論