1、圖像噪聲的成因

圖像在生成和傳輸過程中常常因受到各種噪聲的干擾和影響而是圖像降質，這對后續圖像的處理和圖像視覺效應將產生不利影響。噪聲種類很多，比如:電噪聲，機械噪聲，信道噪聲和其他噪聲。因此，為了抑制噪聲，改善圖像質量，便于更高層次的處理，必須對圖像進行去噪預處理。

2、圖像噪聲的特征

圖像噪聲使得圖像模糊，甚至淹沒圖像特征，給分析帶來困難。

圖像噪聲一般具有以下特點：

噪聲在圖像中的分布和大小不規則，即具有隨機性。

噪聲與圖像之間一般具有相關性。例如，攝像機的信號和噪聲相關，黑暗部分噪聲大，明亮部分噪聲小。又如，數字圖像中的量化噪聲與圖像相位相關，圖像內容接近平坦時，量化噪聲呈現偽輪廓，但圖像中的隨機噪聲會因為顫噪效應反而使量化噪聲變得不很明顯。

噪聲具有疊加性。在串聯圖像傳輸系統中，各部分竄入噪聲若是同類噪聲可以進行功率相加，依次信噪比要下降。

3、圖像噪聲的分類

3.1加性噪聲和乘性噪聲

按噪聲和信號之間的關系，圖像噪聲可分為加性噪聲和乘性噪聲。為了分析處理方便，往往將乘性噪聲近似認為是加性噪聲，而且總是假定信號和噪聲是互相獨立的。

假定信號為S(t)，噪聲為n(t)，如果混合疊加波形是S(t)+n(t)的形式，則稱其為加性噪聲。加性嗓聲和圖像信號強度是不相關的，如圖像在傳輸過程中引進的“信道噪聲”電視攝像機掃描圖像的噪聲等。

如果疊加波形為S(t)［1+n(t)］的形式，則稱其為乘性噪聲。乘性噪聲則與信號強度有關，往往隨圖像信號的變化而變化，如飛點掃描圖像中的嗓聲、電視掃描光柵、膠片顆粒造成等。

3.2 外部噪聲和內部噪聲

按照產生原因，圖像噪聲可分為外部噪聲和內部噪聲。外部噪聲，即指系統外部干擾以電磁波或經電源串進系統內部而引起的噪聲。如外部電氣設備產生的電磁波干擾、天體放電產生的脈沖干擾等。由系統電氣設備內部引起的噪聲為內部噪聲，如內部電路的相互干擾。內部噪聲一般又可分為以下四種：(1)由光和電的基本性質所引起的噪聲。(2)電器的機械運動產生的噪聲。(3)器材材料本身引起的噪聲。(4)系統內部設備電路所引起的噪聲。

3.3 平穩噪聲非平穩噪聲

按照統計特性，圖像噪聲可分為平穩噪聲和非平穩噪聲。統計特性不隨時間變化的噪聲稱為平穩噪聲。統計特性隨時間變化的噪聲稱為非平穩噪聲。

3.4其它幾類噪聲

量化嗓聲是數字圖像的主要噪聲源，其大小顯示出數字圖像和原始圖像的差異，減少這種嗓聲的最好辦法就是采用按灰度級概率密度函數選擇化級的最優化措施。

“椒鹽”噪聲：此類嗓聲如圖像切割引起的即黑圖像上的白點，白圖像上的黑點噪聲，在變換域引入的誤差，使圖像反變換后造成的變換噪聲等。

按噪聲幅度隨時間分布形狀來定義，如其幅度分布是按高斯分布的就稱其為高斯噪聲，而按雷利分布的就稱其為雷利噪聲。

按噪聲頻譜形狀來命，如頻譜均勻分布的噪聲稱為白噪聲；頻譜與頻率成反比的稱為1/f 噪聲；而與頻率平方成正比的稱為三角噪聲等等。

根據經常影響圖像質量的噪聲源又可分電子噪聲和光電子噪聲。

電子噪聲：在阻性器件中由于電子隨機熱運動而造成的電子噪聲是三種模型中最簡單的。

光電子噪聲：光電子噪聲是由光的統計本質和圖像傳感器中光電轉換過程引起的。

4、圖像的噪聲模型

實際獲得的圖像含有的噪聲，根據不同分類可將噪聲進行不同的分類。從噪聲的概率分布情況來看，可分為高斯噪聲、瑞利噪聲、伽馬噪聲、指數噪聲和均勻噪聲。

4.1 高斯噪聲

由于高斯噪聲在空間和頻域中數學上的易處理性，這種噪聲(也稱為正態噪聲)模型經常被用于實踐中。事實上，這種易處理性非常方便，使高斯模型經常用于臨界情況下 。

高斯隨機變量z的PDF由下式給出：

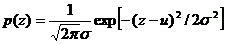
其中z表示灰度值，μ表示z的平均值或期望值，σ表示z的標準差。標準差的平方σ2稱為z的方差。當z服從式（1.3.1）的分布時候，其值有70％落在[(μ-σ),(μ+σ)]內，且有95％落在[(μ-2σ),( μ+2σ)]范圍內。

4.2 瑞利噪聲

瑞利噪聲的概率密度函數由下式給出：

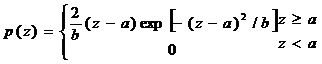
概率密度的均值和方差由下式給出：

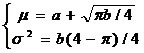
4.3 伽馬(愛爾蘭)噪聲

伽馬噪聲的PDF由下式給出：

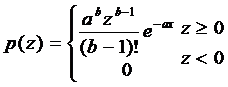
其中，a>0，b為正整數且“!”表示階乘。其密度的均值和方差由下式給出：

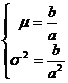
盡管經常被用來表示伽馬密度，嚴格地說，只有當分母為伽馬函數Г(b)時才是正確的。當分母如表達式所示時，該密度近似稱為愛爾蘭密度。

4.4 指數分布噪聲

指數噪聲的PDF可由下式給出：

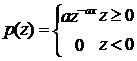
其中a>0。概率密度函數的期望值和方差是：

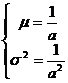
4.5 均勻噪聲分布

均勻噪聲分布的概率密度，由下式給出：

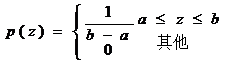
概率密度函數的期望值和方差可由下式給出：

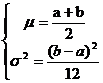
4.6 脈沖噪聲（椒鹽噪聲）

(雙極)脈沖噪聲的PDF可由下式給出：

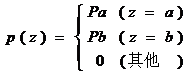
如果b > a，灰度值b在圖像中將顯示為一個亮點，相反，a的值將顯示為一個暗點。若Pa或Pb為零，則脈沖噪聲稱為單極脈沖。如果Pa和Pb均不可能為零，尤其是它們近似相等時，脈沖噪聲值將類似于隨機分布在圖像上的胡椒和鹽粉微粒。由于這個原因，雙極脈沖噪聲也稱為椒鹽噪聲。同時，它們有時也稱為散粒和尖峰噪聲。

噪聲脈沖可以是正的，也可以是負的。標定通常是圖像數字化過程的一部分。因為脈沖干擾通常與圖像信號的強度相比較大，因此，在一幅圖像中，脈沖噪聲總是數字化為最大值(純黑或純白)。這樣，通常假設a，b是飽和值,從某種意義上看，在數字化圖像中，它們等于所允許的最大值和最小值。由于這一結果，負脈沖以一個黑點(胡椒點)出現在圖像中。由于相同的原因，正脈沖以白點(鹽點)出現在圖像中。對于一個8位圖像，這意味著a=0(黑)。b=255(白)。

5、常見圖像去噪算法簡介

圖像噪聲在數字圖像處理技術中的重要性越來越明顯，如高放大倍數航片的判讀，X射線圖像系統中的噪聲去除等已經成為不可缺少的技術步驟。圖像去噪算法可以分為以下幾類：

（1）空間域濾波

空域濾波是在原圖像上直接進行數據運算，對像素的灰度值進行處理。常見的空間域圖像去噪算法有鄰域平均法、中值濾波、低通濾波等。

（2）變換域濾波

圖像變換域去噪方法是對圖像進行某種變換，將圖像從空間域轉換到變換域，再對變換域中的變換系數進行處理，再進行反變換將圖像從變換域轉換到空間域來達到去除圖像嗓聲的目的。將圖像從空間域轉換到變換域的變換方法很多，如傅立葉變換、沃爾什-哈達瑪變換、余弦變換、K-L變換以及小波變換等。而傅立葉變換和小波變換則是常見的用于圖像去噪的變換方法。

（3）偏微分方程

偏微分方程是近年來興起的一種圖像處理方法，主要針對低層圖像處理并取得了很好的效果。偏微分方程具有各向異性的特點，應用在圖像去噪中，可以在去除噪聲的同時，很好的保持邊緣。偏微分方程的應用主要的一類是一種是基本的迭代格式，通過隨時間變化的更新，使得圖像向所要得到的效果逐漸逼近，以及對其改進后的后續工作。該方法在確定擴散系數時有很大的選擇空間，在前向擴散的同時具有后向擴散的功能，所以，具有平滑圖像和將邊緣尖銳化的能力[5]。偏微分方程在低噪聲密度的圖像處理中取得了較好的效果，但是在處理高噪聲密度圖像時去噪效果不好，而且處理時間明顯高出許多。

（4）變分法

另一種利用數學進行圖像去噪方法是基于變分法的思想，確定圖像的能量函數，通過對能量函數的最小化工作，使得圖像達到平滑狀態，現在得到廣泛應用的全變分TV模型就是這一類。這類方法的關鍵是找到合適的能量方程，保證演化的穩定性，獲得理想的結果。

（5）形態學噪聲濾除器

將開與閉結合可用來濾除噪聲，首先對有噪聲圖像進行開運算，可選擇結構要素矩陣比噪聲尺寸大，因而開運算的結果是將背景噪聲去除；再對前一步得到的圖像進行閉運算，將圖像上的噪聲去掉。據此可知，此方法適用的圖像類型是圖像中的對象尺寸都比較大，且沒有微小細節，對這類圖像除噪效果會較好。