自由曲面光學是照明行業在光線重定向到目標區域方面的改變者。非均勻有理B樣條，通常稱為NURBS廣泛用于表示自由曲面和曲面。有一些光學系統需要在設計或優化階段對表面進行局部修飾。在這種情況下，NURBS不能提供這種轉換。但是一個叫做T-splines的新數學表達式使得這是可行的。雖然它的潛力已被很好地描述，但迄今為止尚未在任何優化程序中實施。Annie Shalom Isaac，來自卡爾斯魯厄理工學院的Jiayi Long和Cornelius Neumann通過在優化程序中執行T型樣條證明了局部細化能力的優勢，并對結果進行了評估。結果表明，與NURBS相比，T樣條提供更均勻和均勻的光分布，且收斂速度更快。這使得使用T樣條的光學設計或優化成為未來自由形式設計任務的直觀方法。

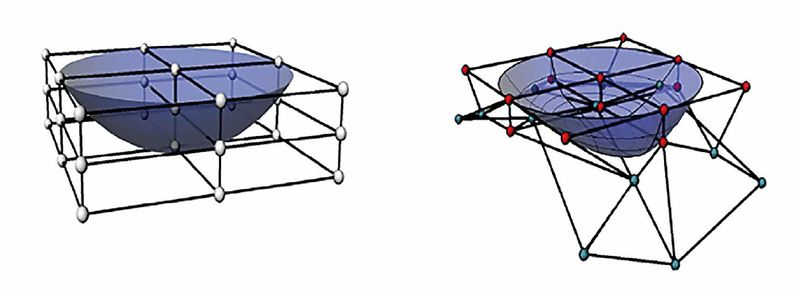
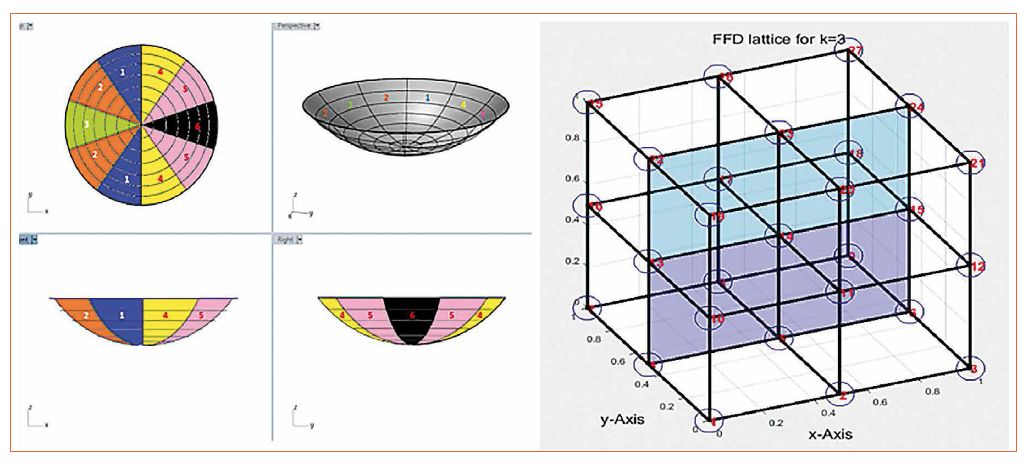
3x3 OFFD柵格在（左）和（右）變形之前封閉和光學表面

自由形式光學器件的設計在很大程度上依賴于以下方法之一：基于點源假設[3]，SMS設計[4]和基于等通量網格[5]的源目標圖的裁剪以創建初始光學表面。由于這些數學方法不能保證為擴展的LED光源提供準確的結果，也不能提供通用的解決方案，光學設計師仍然依靠任何優化工具來改善結果。光線跟蹤算法中的速度提高以及復雜的智能優化算法使優化方法的應用更加廣泛。但自由曲面優化的缺點主要是由于其復雜的數學表達和許多參數的存在。

Wendel et.al提出了一種稱為優化的方法，使用自由形變（OFFD）來克服這個困難，將光學表面置于網格中并使封閉的網格變形而不是直接作用于網格[1]。這種方法使用NURBS來表示光學表面，其結果表明，使用較少的優化變量，它們可以很好地實現全局變形，這使得制造更容易。但是有些情況下需要在光線分布上有明顯的傾斜，或者光線的路徑必須顯著改變。在這種情況下，輕微的局部變形會帶來顯著的改善。但是對于目前的OFFD，這是不可能的，因為下面的表面表示。稱為T樣條的另一種表面表示法可以克服這個缺點[2]。Bailey等人。al已經證明了T-splines的潛力及其在光學表面的應用[6]。但是迄今為止，這種方法既未應用于任何優化程序，也未對其光學性能進行分析并與NURBS進行比較。

因此，這項工作考慮了這個問題，并提供了解決這個問題的替代方法。第2部分介紹了OFFD技術。光學表面的數學表面表示在第3節中介紹.T樣條的實現結果和比較結果在第4節中顯示，隨后在第5節中給出結論。

使用OFFD進行優化

OFFD方法采用Sederberg [7]提出的自由變形（FFD）技術，并結合優化程序。網格和光學表面之間的關系使用FFD算法很好地建立[7]。圖1顯示了在變形之前和之后具有光學表面的網格。為了簡潔起見，只介紹OFFD方法的概述。

該算法首先選擇一個輸入表面，其光學性能必須得到改善，這通常遠離目標。通過這種方法，光學表面被包圍在包含27個網格控制點的網格內，并且用戶可以從它們中選擇任何組合。這作為變量提供給優化算法。優化算法對于選定的網格點組合具有廣泛的搜索空間，并提供沿三維向封閉網格的移動。隨著封閉的網格發生變化，它也會改變其內部的光學表面。然后對變形后的表面進行光度評估，優化算法根據此結果決定其優化變量的變化。該算法一再重復，直到達到目標照明要求。

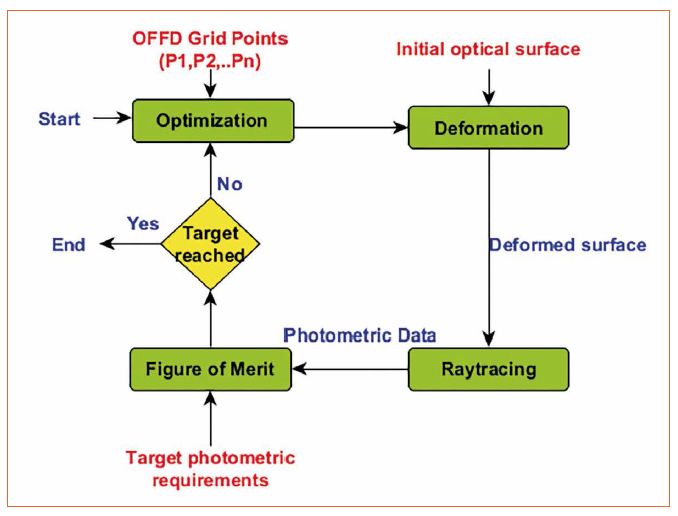
這個程序中最重要的一步是變形光學表面的品質因數定義，因為整個優化是基于這個單一的值，稱為Q.在本文中，我們使用兩個不同的評價函數。

偏差評價函數Qdev，其對應于當前模擬分布與期望分布的偏差并被表示為

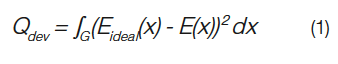
G是人們感興趣的區域，Eideal（x）是期望的照度分布目標，E（x）是當前的光分布。

通量擇優函數Q磁通對應于最大化，其中被量化為在目標（Φ通量的比率所需的目標區域中的通量噸），并通過光學器件收集φC可用通量。

光學表面的數學表示

NURBS

NURBS技術非常成熟，可用于計算機輔助圖形系統以及光線追蹤器。由于其靈活性，可以通過在優化程序期間更改控制點或其重量來輕松操縱或修改曲面。NURBS曲面是參數張量積曲面，定義如下：

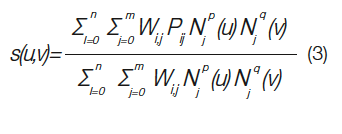
其中Pij是控制點的矩形陣列，其中Pij是（n + 1）×（m + 1）矩陣，wi，j是權重，Nip（u）和Njq（v）是u和p的基函數， v方向，分別與結矢量相關聯。

其中r = p + n + 1和s = m + q + 1成立。當必須在NURBS中添加控制點時，使用結插入方法完成控制點。添加單個節點需要添加整列或一排控制點。使用NURBS也不可能去除結頭，而不會改變幾何形狀。這種局部細化主要限于NURBS，因為它的張量產品結構如EQ3所示。如圖3所示，NURBS曲面被逐列水平和垂直逐行地重復。為了滿足這種平衡，如果增加一個新的控制點，則同時添加整列或一行控制點。

T樣條

由NURBS強加的缺點可以通過稱為T樣條的自由曲面的替代數學表示來解決。T型樣條概括了B樣條，通過向圖3中相關的B樣條添加T型結，將特定的行和列參數分配給特定的控制點。這使得T樣條在局部變形中是一種更先進的技術，不需要的控制點。T樣條是基于點而不是基于網格的張量積B-樣條。控制網格稱為T網格，T樣條曲面的定義由下式給出

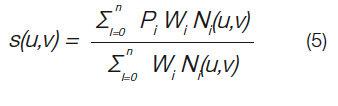
其中Pi是控制點。Ni（u，v）是基本函數，由下式給出

基本函數Nui（u）和Nvi（v）分別與結向量相關聯

當一個人插入一個新的控制點或一個結時，其他控制點之間的間隔必須被改進而不會改變其形狀。這是通過滿足EQ6分別對兩個單變量基函數Nui（u）和Nvi（v）進行細化來完成的。這種局部細化的性質不會增加控制點的數量，也不會改變幾何圖形使T型樣條自然成為在OFFD中實現并實現局部變形的理想選擇。

T形樣條在OFFD中的應用

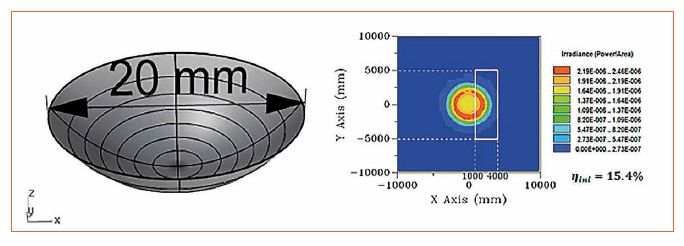
最后一節介紹了T樣條的理論背景和在局部變形中使用它的優點。本節介紹T形樣條在第2節簡要介紹的自由形變系統優化程序中的應用。在我們的例子中，我們使用了與[1]中使用的設計路燈透鏡相同的光學設計任務。將具有100流明的Cree XPG2 LED用作光源，并且優化前的初始表面如圖4所示。為了評估光度性能，應用等式1和2中表達的評價函數。

要在OFFD中開始T-spline實現，必須在所需區域添加更多控制點，并且曲面形狀保持不變。在更多和更密集的控制點聚集的區域內實現更多的局部變形。然后進行研究以發現變形過程對透鏡的哪個部分更多的影響，以及如果該部分上的敏感局部變形導致更好的結果。

整個光學表面分為六個部分，如圖4所示。此步驟基于直觀的假設。y方向的對稱性是由于目標街道和燈停留在y方向的中間（圖5）。為了直接比較，選擇網格點[1,3,13,15]。更多的控制點被添加到從1到6的每個片段中。最后，生成了六個新的光學曲面。這些生成的新T樣條曲面與初始曲面之間的唯一區別是控制點數量的差異。光學器件的形狀保持不變，沒有任何預期的變化。這些光學表面一個接一個地作為OFFD的初始表面，并使用所述的優點函數進行評估。初步的結果表明，當更多的控制點被添加到分段5時，可以看到對光分布的更多影響。因此，在分段5處具有更多控制點并且在其余分段處具有更少控制點的光學表面被視為用于優化的初始系統并且與NURBS進行比較。然后將這個結果與基于NURBS的OFFD進行比較，結果在下一節中討論。

初始系統

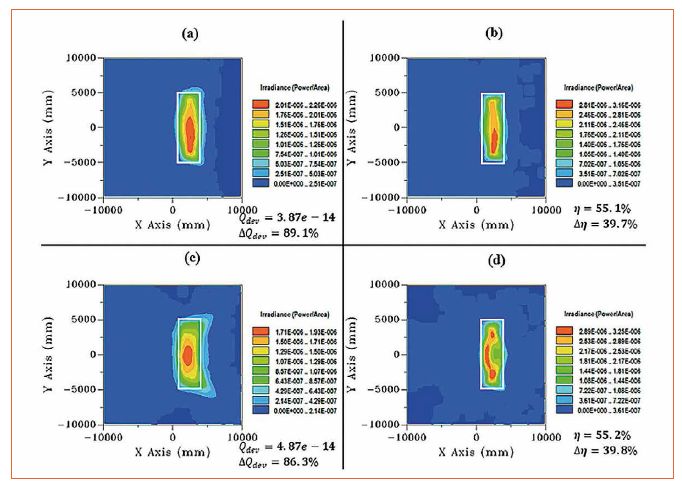
的性能初始表面的光學性能如圖6所示，只有目標內部總通量的15％，并且分布形狀遠離需要的標記為白色的矩形分布。

NURBS與T樣條的比較

用于比較用于分析街道照明鏡頭的NURBS和T-splines的兩個重要光度測量方法是目標中的總光通量，并且均勻照明分布在目標上。NURBS和T-splines在同一水平上執行目標中的總光通量，發現其為55％，如圖7b和7d所示，產生40％的改善（Δn）。但是T樣條在根據需要塑造目標分布方面的表現要優于圖7a中的模擬結果。如圖7b所示，使用T樣條的照度分布比具有NURBS的分布更均勻。使用NURBS和T樣條的變形光學曲面如圖8所示。略微不同的是在邊緣附近的T型樣條，在圖4中標記為段5。

如果使用NURBS需要獲得相同的結果，則網格中的控制點對用戶的選擇更為敏感。當準確選擇時，可以獲得這些結果，但代價是優化的運行時間很長 - 幾乎是使用T樣條所需時間的兩倍。使用T樣條的最大優點是當用戶知道光學表面的局部變形部分時，他可以對網格中控制點的選擇產生最小的困擾。

結論

這項工作突出了T形樣條的使用，通過在優化程序中首次實現光學曲面的局部變形。結果表明，使用T樣條可以獲得比NURBS更均勻的光分布。當使用T型樣條時，FFD網格點的靈敏度會降低。這對智能優化系統非常重要。由于T樣條曲線是更高級的曲面表示，所以它尚未成熟。CAD技術和光線追蹤器尚未達到導入的程度，并且直接使用T-splines文件格式。所以在本文發表時，人們仍然需要依靠T樣條向NURBS的前后轉換來執行光線追蹤。另一個限制因素，但并不是很大，因為控制點必須在需要的地方更精確地加入。