摘要:
由于船舶動力定位控制系統是一個復雜的非線性系統,常規整定的PID參數難以取得理想的控制效果,由此提出將免疫類電磁機制(IEM)算法用于PID控制器的參數自整定。針對類電磁機制(EM)算法易陷入局部最優的缺陷,引入免疫信息處理機制,利用其特有的濃度選擇機制保留優良的粒子并通過免疫算子使粒子靠近最優位置。使用IEM、EM和PSO算法整定PID控制器參數,分析結果可以得出IEM算法具有更優的穩定性、更高的收斂精度。最后在IEM-PID和常規PID控制器作用下分別對船舶DP的位置和艏向進行仿真,仿真結果表明,相比常規PID控制器,IEM-PID控制器響應速度更快、穩定性更優、穩態誤差更小。
0 引言
近年來我國船舶工業和海洋事業處在高速發展期,船舶動力定位仍是一大研究熱點。與傳統的錨泊定位相比,動力定位因其定位精度高、機動性強且不受水深限制等優點,在海洋開發中備受青睞[1]。PID控制器作為最早被應用在船舶動力定位系統上的控制器,對于DP船舶控制精度要求特別高的系統,效果并不理想。最先應用于PID自整定的算法是Z-N PID整定法[2],隨后神經網絡[3]、遺傳算法[4]、粒子群算法[5]等一系列算法都較好地提高了PID控制的適應性,但也存在許多不足,如控制易出現超調、振蕩激烈或者策略復雜等。
類電磁機制(Electromagnetism-like Mechanism,EM)算法是由Birbil和Fang在2003年首次提出的一種基于人工智能的隨機全局優化算法。該算法的優勢在于具有簡單的尋優機理、響應速度快、所需資源較少因而容易實現等,但是算法運行后期也存在會陷入局部最優的缺陷。為此,姜建國等人采用混沌-模式搜索方法,能有效跳出局部極值點進行局部搜索,但其搜索結果的好壞很大程度上依賴于初始點的選擇[6];TAN J D等人提出了SPC的新搜索方案,設計一個非線性方程式,根據每次迭代中比較段的結果動態調整探針長度跳出局部最優,但是算法結構復雜,運行成本大大增加[7]。
針對以上問題,本文提出一種免疫類電磁機制(Immune Electromagnetism-like Mechanism,IEM)算法。PID控制器kp、ki、kd3個參數由IEM算法進行自整定,并與EM算法和粒子群優化(PSO)算法的仿真結果進行比較,驗證了IEM算法的有效性。最后將基于IEM算法的船舶動力定位PID控制器進行仿真,仿真結果表明改進過后的控制器具有更好的控制效果。
1 船舶運動模型
1.1 船舶運動數學模型
船舶處于航向保持、航跡保持的操縱運動和動力定位中的定點位置保持時,可認為船舶只作三自由度的平面運動[8]。當只執行位置保持功能時速度值很小,科氏向心力和非線性阻尼可以忽略[9]。所以船舶動力定位低頻運動數學模型為:

1.2 動力定位控制對象模型
現以一艘拖輪為受控對象,船舶參數如表1所示,附加質量的慣性矩陣和阻尼矩陣分別為:
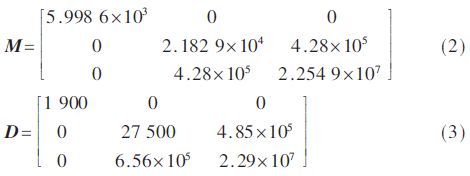
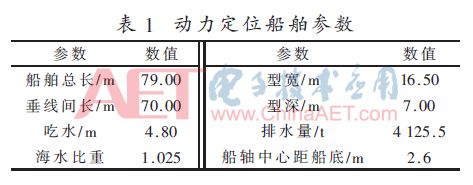
在動力定位系統中,由常規試湊法得到的三自由度PID控制參數為:
縱蕩:kp=156.07,ki=0.38,kd=115.78
橫蕩:kp=114.15,ki=0.01,kd=175.87
艏搖:kp=4 645.43,ki=1.561,kd=147 127.54
由于常規PID控制器難以達到理想的控制效果,因此需要對PID控制參數進行整定。
2 IEM算法整定PID參數
2.1 EM算法
EM算法分成4個步驟,即初始化、局部搜索、計算合力和移動粒子[10]。帶電粒子xi在EM算法中電荷量的計算公式如下:

2.2 IEM算法
為了解決EM算法后期容易陷入局部最優的缺陷,將生物免疫機制引入到算法中。該機制中,抗原代表了求解問題的目標函數,而抗體代表了問題的解[11-12]。在每次迭代過程中,除了EM算法的更新公式內產生N個粒子,還隨機生成滿足約束條件的M個粒子,以此來增加粒子的多樣性。采用基于濃度機制的多樣性保持策略,使得新一代粒子群體中各適應度層次的粒子維持一定的濃度。第i個粒子(抗體)的濃度定義為:

式(9)中粒子i被選中的概率和與該粒子相似的粒子數量成反比,其意義就在于即使粒子對應的適應度值較低,也有機會得到進化,從而保證了群體的多樣性。
IEM算法的實現步驟如下:
(1)確定IEM算法的參數值,包括:種群規模N、種群維度n、最大迭代次數Maxgeneration、最小適應值minfit;
(2)隨機生成N個粒子,形成初始種群,根據適應度函數計算出種群的適應值,將當前目標函數值f(xi)最優的粒子記為xbest;
(3)對最優粒子進行局部搜索;
(4)利用式(4)和式(5)分別計算出粒子的電荷量以及粒子間的作用力;
(5)根據式(6)移動粒子,找出粒子位置更新后的最優粒子,并將對應的位置粒子存入記憶庫;
(6)隨機生成M個粒子,同步驟(2),根據式(9)從N+M個粒子中依據選取概率大小來選取N個粒子;
(7)根據最小適應值和最大迭代次數判斷是否迭代結束,并輸出符合條件的最優粒子,否則轉至步驟(3)。
2.3 IEM算法性能分析
本文選用兩個具有不同特征的典型測試函數對改進后的算法進行測試,來驗證IEM算法的優越性:
(1)Schwefel函數:
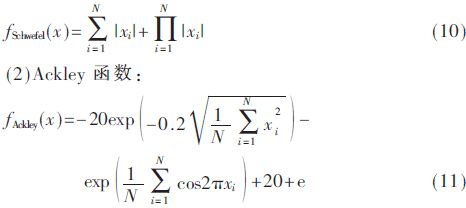
具體參數設置如下:種群規模N=20,種群維度n=10,最大迭代次數Maxgeneration=500,標準PSO算法中學習因子c1=c2=2,慣性因子ω=1。
圖1為兩個測試函數在不同算法優化后繪制成的迭代曲線。從圖中可以看出,IEM算法無論在單峰Schwefel函數還是多峰Ackley函數中都具有較快的收斂速度。
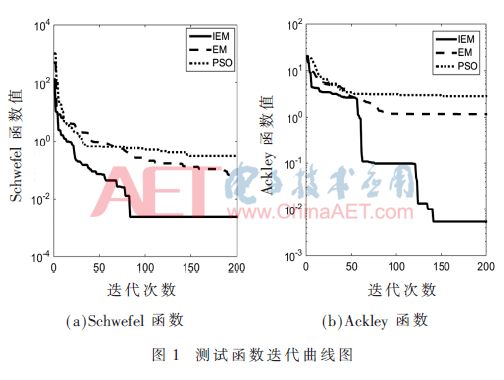
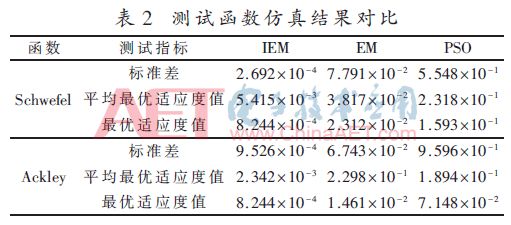
表2為優化的結果數據,測試指標中的標準差可以用來評估算法的穩定性,而最優適應值和平均最優適應值可以用來分析算法的精度。從表中可以看出,IEM算法相比EM和PSO算法,在不同測試指標上均有數量級上的提升,因此IEM算法的穩定性更優,收斂精度更高。
2.4 IEM算法整定PID控制參數
本文分別用IEM算法、EM算法以及PSO算法對PID的參數進行了尋優,并通過時域性能指標來比較各算法尋優過后的階躍響應。適應度函數選用ITAE指標:

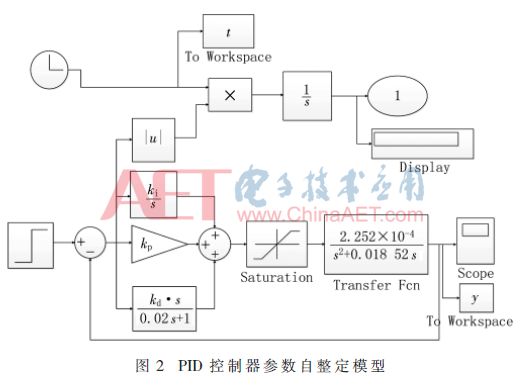
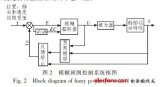
以拖輪縱蕩作為被控對象,在Simulink環境下建立的模型如圖2所示。圖中,輸出端口1為式(12)所示的ITAE指標。在PID參數自整定過程中,將控制器的一組三維參數(kp,ki,kd)作為IEM算法的一個粒子,PID參數的整定轉換為三維粒子的函數優化問題,通過IEM隨機產生的粒子,依次對應各組參數,運行Simulink模型后可以得到各組參數的性能指標,并將其傳遞到IEM算法中對應粒子的適應度值。
仿真實驗中,IEM算法參數選取如下:種群規模N=50,最大迭代次數Maxgeneration=100,種群維度n=3,最小適應值minfit=0.1;標準PSO算法中學習因子c1=c2=2,慣性因子ω=0.6。
表3列出了IEM、EM、PSO 3種算法整定過后的kp、ki和kd參數及性能指標。可以看出,IEM算法對PID控制器參數進具有更好的整定效果。
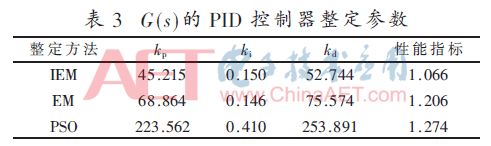
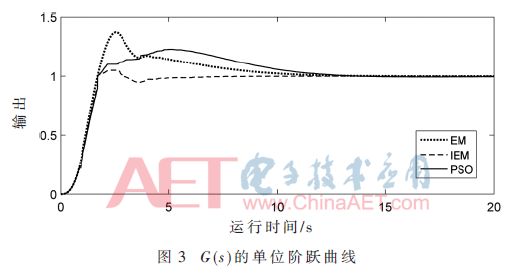
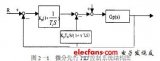
圖3為IEM、EM、PSO 3種算法在控制對象G(s)的單位階躍響應曲線。由圖可知,采用IEM算法整定的PID控制器具有較快的響應速度、較短的調節時間,且超調和穩態誤差也最小。
3 IEM-PID動力定位控制器仿真分析
以拖輪為對象,利用IEM算法對PID控制器的參數進行整定。取種群規模N=50,種群維度n=3,最大迭代次數Maxgeneration=100,最小適應值minfit=0.1。控制參數整定結果為:
縱蕩:kp=45.22,ki=0.15,kd=52.74
橫蕩:kp=55.13,ki=0.026,kd=76.62
艏搖:kp=3 976.78,ki=1.237,kd=131 799.54
為驗證所設計的IEM-PID控制器性能,將其控制船舶三自由度運動效果,并與傳統PID控制器在相同情況下進行對比。船舶起始位置為η=[0,0,0],給定船舶的期望位置為η=[20,30,10],仿真時間為500 s,仿真結果如圖4所示。
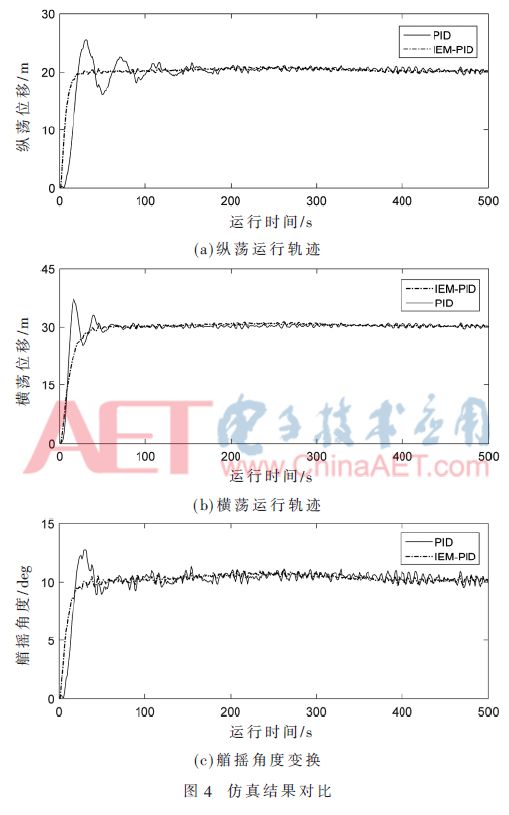
由圖4仿真結果可知,傳統PID控制在縱蕩、橫蕩、艏搖3個方向上響應的調節時間和超調量分別為123 s、61 s、58 s和30.24%、23.33%、29.3%。IEM-PID在這3個方向的調節時間分別為21 s、38 s、27 s,且在3個方向的響應曲線無超調。可見,IEM-PID控制器在調節時間、超調量以及穩態精度上都有顯著提高,不僅能夠滿足控制需求,而且其控制效果也比傳統PID更加優越。
4 結論
控制器的控制效果決定著船舶動力定位系統的精度和穩定性。IEM-PID控制器中的免疫類電磁機制算法基于濃度選擇機制的粒子選擇策略保留優良粒子,防止了算法優化性能退化。仿真結果表明,改進后的控制器在較大程度上提高了控制系統性能,有一定的實用價值。
-
控制器
+關注
關注
112文章
16203瀏覽量
177412 -
定位系統
+關注
關注
10文章
576瀏覽量
36449 -
PID
+關注
關注
35文章
1471瀏覽量
85289
原文標題:【學術論文】基于IEM的動力定位PID控制器參數整定
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于遺傳算法的PID 控制及其MATLAB 仿真
如何使用DSP進行數字PID控制器的設計
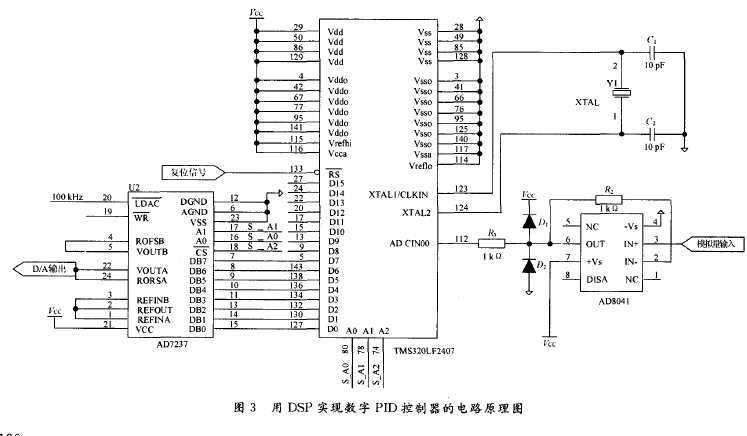
如何使用MTALAB的模糊PID控制器進行設計與仿真的研究
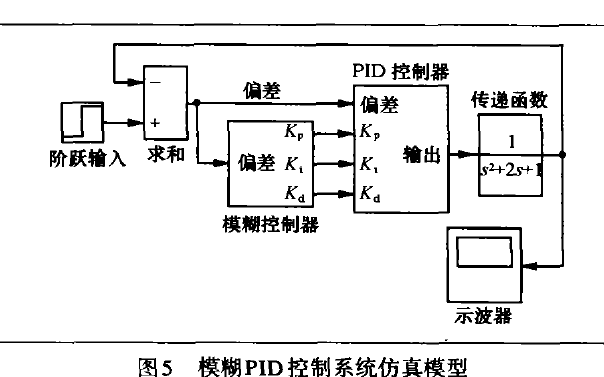
如何才能實現自校正PID控制器詳細資料與仿真分析
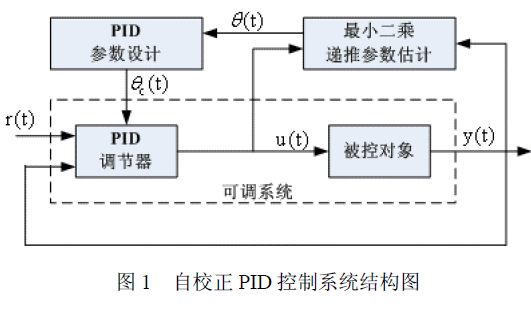




 基于IEM算法的船舶動力定位PID控制器進行仿真
基于IEM算法的船舶動力定位PID控制器進行仿真











評論