所有的機器學習算法都或多或少的依賴于對目標函數最大化或者最小化的過程。我們常常將最小化的函數稱為損失函數,它主要用于衡量模型的預測能力。在尋找最小值的過程中,我們最常用的方法是梯度下降法,這種方法很像從山頂下降到山谷最低點的過程。
雖然損失函數描述了模型的優劣為我們提供了優化的方向,但卻不存在一個放之四海皆準的損失函數。損失函數的選取依賴于參數的數量、局外點、機器學習算法、梯度下降的效率、導數求取的難易和預測的置信度等方面。這篇文章將介紹各種不同的損失函數,并幫助我們理解每種函數的優劣和適用范圍。
由于機器學習的任務不同,損失函數一般分為分類和回歸兩類,回歸會預測給出一個數值結果而分類則會給出一個標簽。這篇文章主要集中于回歸損失函數的分析。
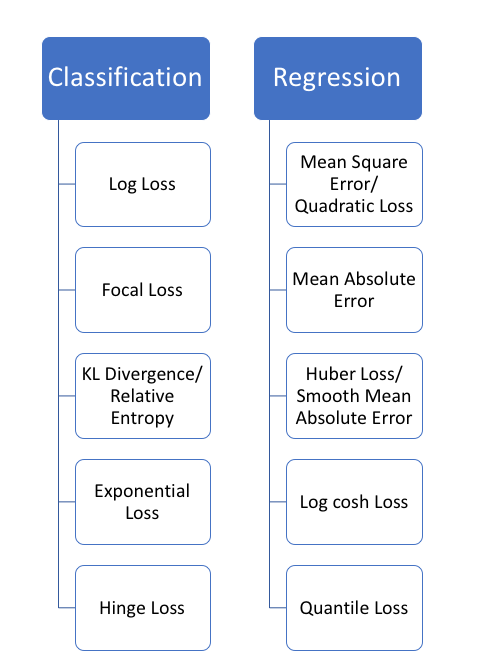
1.均方誤差、平方損失——L2損失
均方誤差(MSE)是回歸損失函數中最常用的誤差,它是預測值與目標值之間差值的平方和,其公式如下所示:
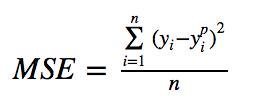
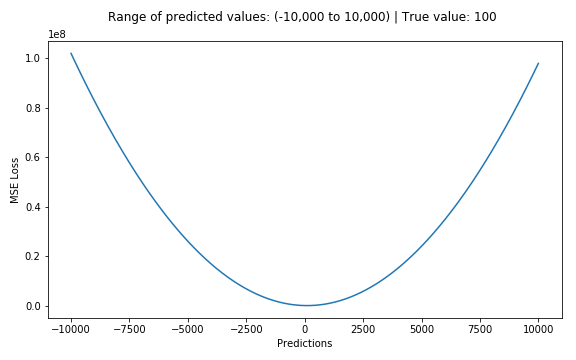
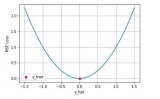
下圖是均方根誤差值的曲線分布,其中最小值為預測值為目標值的位置。我們可以看到隨著誤差的增加損失函數增加的更為迅猛。
2.平均絕對誤差——L1損失函數
平均絕對誤差(MAE)也是一種常用的回歸損失函數,它是目標值與預測值之差絕對值的和,表示了預測值的平均誤差幅度,而不需要考慮誤差的方向(注:平均偏差誤差MBE則是考慮的方向的誤差,是殘差的和),其公式如下所示:
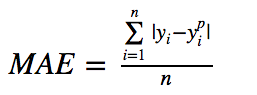
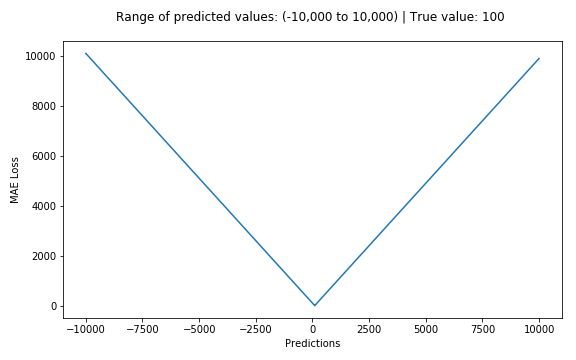
平均絕對誤差和均方誤差(L1&L2)比較
通常來說,利用均方差更容易求解,但平方絕對誤差則對于局外點更魯棒,下面讓我們對這兩種損失函數進行具體的分析。
無論哪一種機器學習模型,目標都是找到能使目標函數最小的點。在最小值處每一種損失函數都會得到最小值。但哪種是更好的指標呢?讓我們用具體例子看一下,下圖是均方根誤差和平均絕對誤差的比較(其中均方根誤差的目的是與平均絕對誤差在量級上統一):
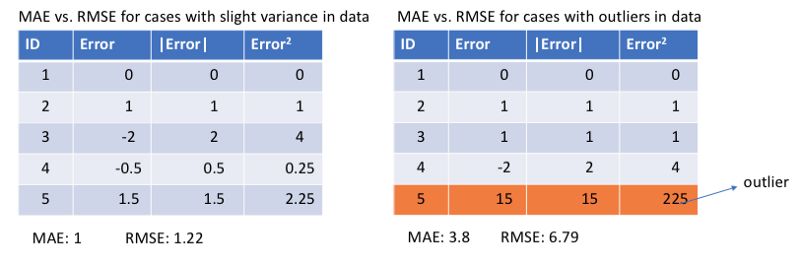
左邊的圖中預測值與目標值很接近,誤差與方差都很小,而右邊的圖中由于局外點的存在使得誤差變得很大。
由于均方誤差(MSE)在誤差較大點時的損失遠大于平均絕對誤差(MAE),它會給局外點賦予更大的權重,模型會致力減小局外點造成的誤差,從而使得模型的整體表現下降。
所以當訓練數據中含有較多的局外點時,平均絕對誤差(MAE)更為有效。當我們對所有觀測值進行處理時,如果利用MSE進行優化則我們會得到所有觀測的均值,而使用MAE則能得到所有觀測的中值。與均值相比,中值對于局外點的魯棒性更好,這就意味著平均絕對誤差對于局外點有著比均方誤差更好的魯棒性。
但MAE也存在一個問題,特別是對于神經網絡來說,它的梯度在極值點處會有很大的躍變,及時很小的損失值也會長生很大的誤差,這不利于學習過程。為了解決這個問題,需要在解決極值點的過程中動態減小學習率。MSE在極值點卻有著良好的特性,及時在固定學習率下也能收斂。MSE的梯度隨著損失函數的減小而減小,這一特性使得它在最后的訓練過程中能得到更精確的結果。
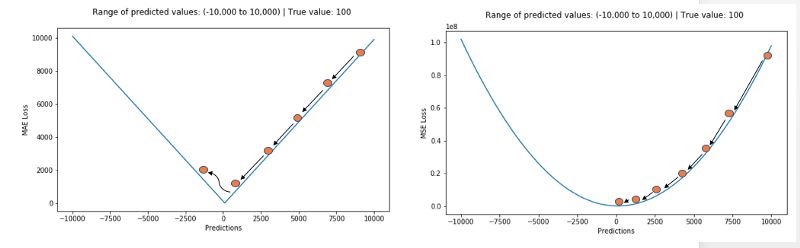
在實際訓練過程中,如果局外點對于實際業務十分重要需要進行檢測,MSE是更好的選擇,而如果在局外點極有可能是壞點的情況下MAE則會帶來更好的結果。(注:L1和L2一般情況下與MAE和MSE性質相同)
總結:L1損失對于局外點更魯棒,但它的導數不連續使得尋找最優解的過程低效;L2損失對于局外點敏感,但在優化過程中更為穩定和準確。
但現實中還存在兩種損失都很難處理的問題。例如某個任務中90%的數據都符合目標值——150,而其余的10%數據取值則在0-30之間。那么利用MAE優化的模型將會得到150的預測值而忽略的剩下的10%(傾向于中值);而對于MSE來說由于局外點會帶來很大的損失,將使得模型傾向于在0-30的方向取值。這兩種結果在實際的業務場景中都是我們不希望看到的。
那怎么辦呢?
讓我們來看看其他的損失函數吧!
3.Huber損失——平滑平均絕對誤差
Huber損失相比于平方損失來說對于局外點不敏感,但它同樣保持了可微的特性。它基于絕對誤差但在誤差很小的時候變成了平方誤差。我們可以使用超參數δ來調節這一誤差的閾值。當δ趨向于0時它就退化成了MAE,而當δ趨向于無窮時則退化為了MSE,其表達式如下,是一個連續可微的分段函數:
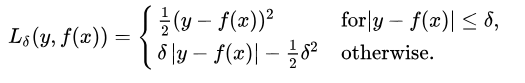
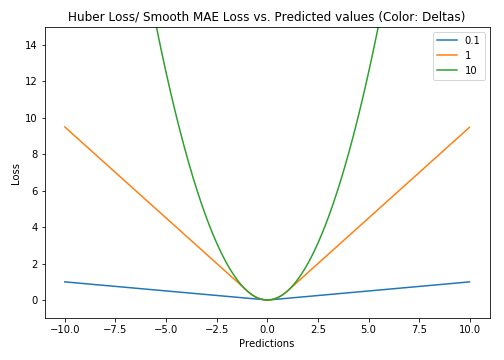
對于Huber損失來說,δ的選擇十分重要,它決定了模型處理局外點的行為。當殘差大于δ時使用L1損失,很小時則使用更為合適的L2損失來進行優化。
Huber損失函數克服了MAE和MSE的缺點,不僅可以保持損失函數具有連續的導數,同時可以利用MSE梯度隨誤差減小的特性來得到更精確的最小值,也對局外點具有更好的魯棒性。
但Huber損失函數的良好表現得益于精心訓練的超參數δ。
4.Log-Cosh損失函數
對數雙曲余弦是一種比L2更為平滑的損失函數,利用雙曲余弦來計算預測誤差:
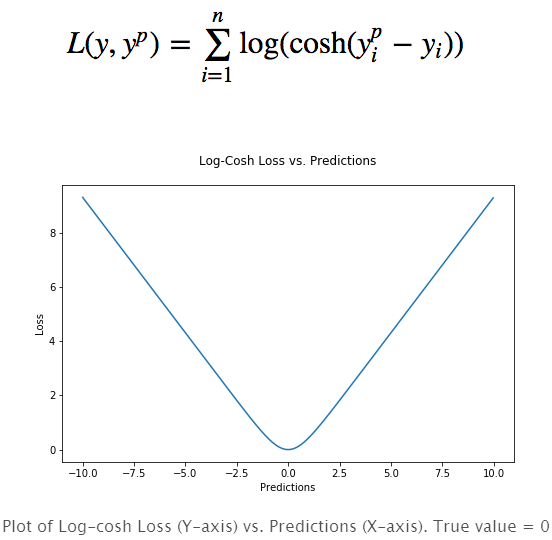
其優點在于對于很小的誤差來說log(cosh(x))與(x**2)/2很相近,而對于很大的誤差則與abs(x)-log2很相近。這意味著logcosh損失函數可以在擁有MSE優點的同時也不會受到局外點的太多影響。它擁有Huber的所有優點,并且在每一個點都是二次可導的。二次可導在很多機器學習模型中是十分必要的,例如使用牛頓法的XGBoost優化模型(Hessian矩陣)。

但是Log-cosh損失并不是完美無缺的,它還是會在很大誤差的情況下梯度和hessian變成了常數。
5.分位數損失(Quantile Loss)
在大多數真實世界的預測問題中,我們常常希望得到我們預測結果的不確定度。通過預測出一個取值區間而不是一個個具體的取值點對于具體業務流程中的決策至關重要。
分位數損失函數在我們需要預測結果的取值區間時是一個特別有用的工具。通常情況下我們利用最小二乘回歸來預測取值區間主要基于這樣的假設:取值殘差的方差是常數。但很多時候對于線性模型是不滿足的。這時候就需要分位數損失函數和分位數回歸來拯救回歸模型了。它對于預測的區間十分敏感,即使在非常數非均勻分布的殘差下也能保持良好的性能。下面讓我們用兩個例子看看分位數損失在異方差數據下的回歸表現。
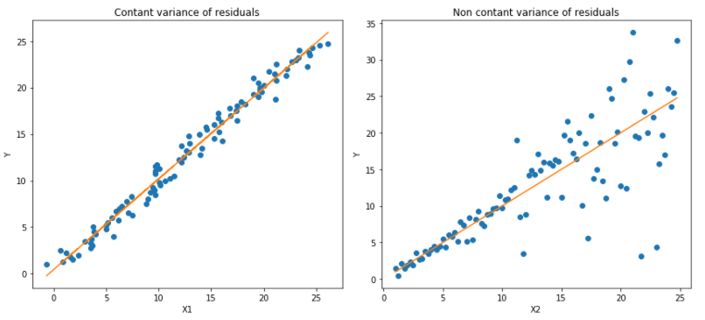
上圖是兩種不同的數據分布,其中左圖是殘差的方差為常數的情況,而右圖則是殘差的方差變化的情況。我們利用正常的最小二乘對上述兩種情況進行了估計,其中橙色線為建模的結果。但是我們卻無法得到取值的區間范圍,這時候就需要分位數損失函數來提供。
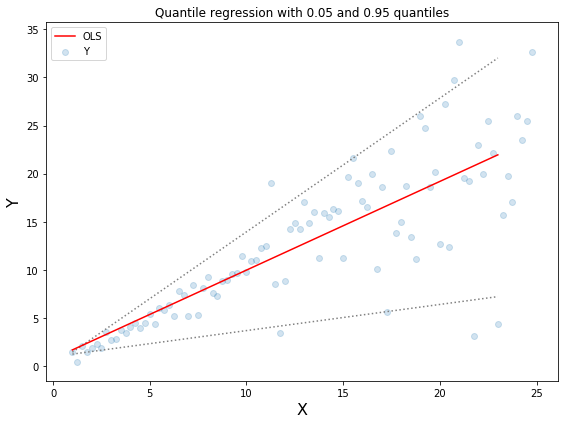
上圖中上下兩條虛線基于0.05和0.95的分位數損失得到的取值區間。從圖中可以清晰地看到建模后預測值得取值范圍。分位數回歸的目標在于估計給定預測值的條件分位數。實際上分位數回歸就是平均絕對誤差的一種拓展(當分位數為第50個百分位時其值就是平均絕對誤差)
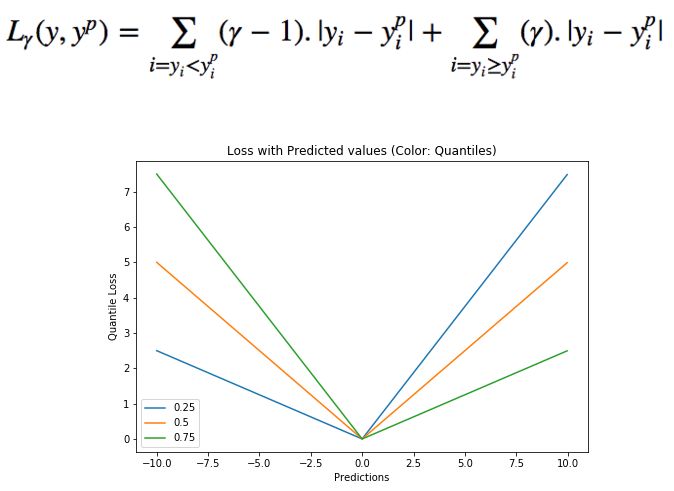
分位數值得選擇在于我們是否希望讓正的或者負的誤差發揮更大的價值。損失函數會基于分位數γ對過擬合和欠擬合的施加不同的懲罰。例如選取γ為0.25時意味著將要懲罰更多的過擬合而盡量保持稍小于中值的預測值。γ的取值通常在0-1之間,圖中描述了不同分位數下的損失函數情況,明顯可以看到對于正負誤差不平衡的狀態。
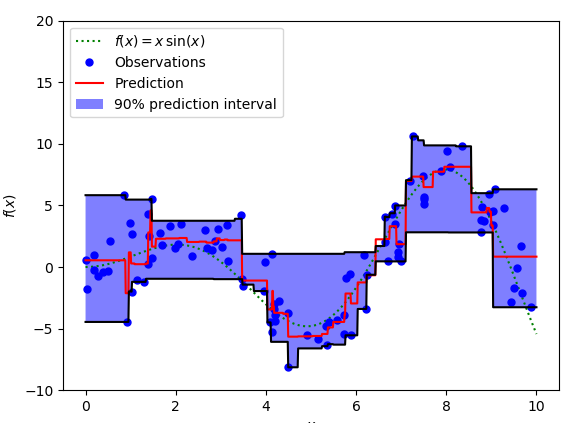
我們可以利用分位數損失函數來計算出神經網絡或者樹狀模型的區間。下圖是計算出基于梯度提升樹回歸器的取值區間。90%的預測值起上下邊界分別是用γ值為0.95和0.05計算得到的。
在文章的最后,我們利用sinc(x)模擬的數據來對不同損失函數的性能進行了比較。在原始數據的基礎上加入而高斯噪聲和脈沖噪聲(為了描述魯棒性)。下圖是GBM回歸器利用不同的損失函數得到的結果,其中ABCD圖分別是MSE,MAE,Huber,Quantile損失函數的結果:
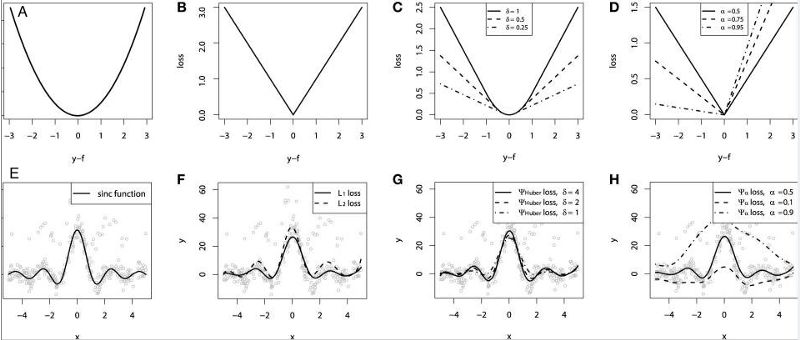
我們可以看到MAE損失函數的預測值受到沖擊噪聲的影響更小,而MSE則有一定的偏差;Huber損失函數對于超參數的選取不敏感,同時分位數損失在對應的置信區間內給出了較好的估計結果。
希望小伙伴們能從這篇文章中更深入地理解損失函數,并在未來的工作中選擇合適的函數來更好更快地完成工作任務。
最后,附上本文中幾種損失函數的簡圖,回味一番:
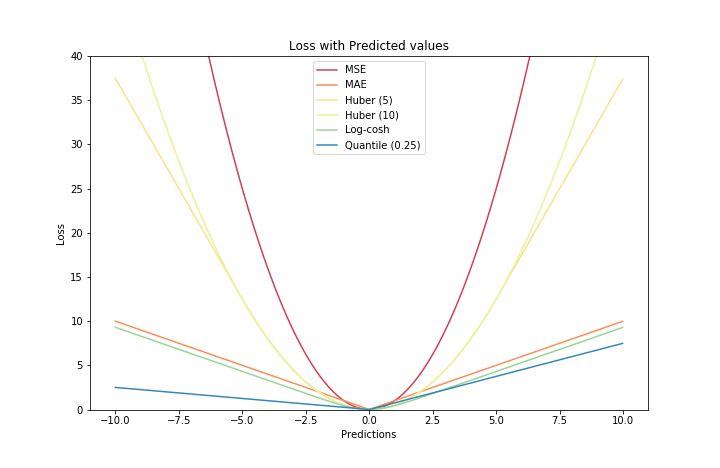
-
函數
+關注
關注
3文章
4308瀏覽量
62445 -
機器學習
+關注
關注
66文章
8382瀏覽量
132444
原文標題:機器學習里必備的五種回歸損失函數
文章出處:【微信號:thejiangmen,微信公眾號:將門創投】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何使用Arm CMSIS-DSP實現經典機器學習庫
神經網絡中的損失函數層和Optimizers圖文解讀
機器學習實用指南:訓練和損失函數




 機器學習經典損失函數比較
機器學習經典損失函數比較

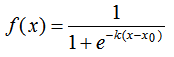










評論