這是一篇八千字的長文,是一些算法筆記的整理集合,希望能給你幫助。
曾經有一個著名的騙局:
小明是一個賭馬愛好者,最近他連續幾次提前收到了預測賭馬結果的郵件,從一開始由于不屑而錯失良機,到漸漸深信不疑,直到最后給郵件發送方匯了巨款才發現上當。
看過這個的人應該知道,騙子收集到一份郵件信息后,分組發送不同預測結果的郵件,賭馬結果公布后,再將篩選出來的那部分人分組,繼續發送下一輪預測郵件。幾輪過后,肯定能保證一部分人收到的預測結果是完全正確的。這也是最關鍵的部分。
那么騙子是如何從幾萬或幾十萬用戶中尋找這些“幸運兒”的呢?這是一種二分法的思想。
假如要順序在100萬人中尋找一個人,最多需要100萬次,而二分法只需要18次。
下面講講一些能夠解決生活中一些具體問題的常用算法。
二分查找
對于一個長度為N的數組,簡單查找最多需要N步;二分查找最多只需要logN步(約定底數為2)。
二分查找相較于簡單查找,極大地提高了效率,但是二分查找的前提是列表是有序的,這也導致了諸多限制。
下面使用二分法編寫一個查找算法。
Python實現
1def binary_search(list,target): 2 #查找的起點和終點 3 low=0 4 high=len(list)-1 5 # 6 while (low<=high): 7 ? ? ? ?#若low+high為奇數,則向下取整 8 ? ? ? ?mid=(low+high)//2 9 ? ? ? ?temp=list[mid]10 ? ? ? ?if target==temp:11 ? ? ? ? ? ?return mid12 ? ? ? ?elif temp>target:13 high=mid-114 else:15 low=mid+116 return None17if __name__ == '__main__':18 test_list=[1,2,4,5,12,32,43]19 print(binary_search(test_list,4))20 print(binary_search(test_list, 44))
輸出結果:
122None
遞歸
想象這么一個問題,在一個大盒子里,有若干個小盒子,在這些小盒子里也可能有更小的盒子。在所有盒子中,其中一個盒子內有一把鑰匙,如何找到這把鑰匙?
有兩種思路:
第一種:
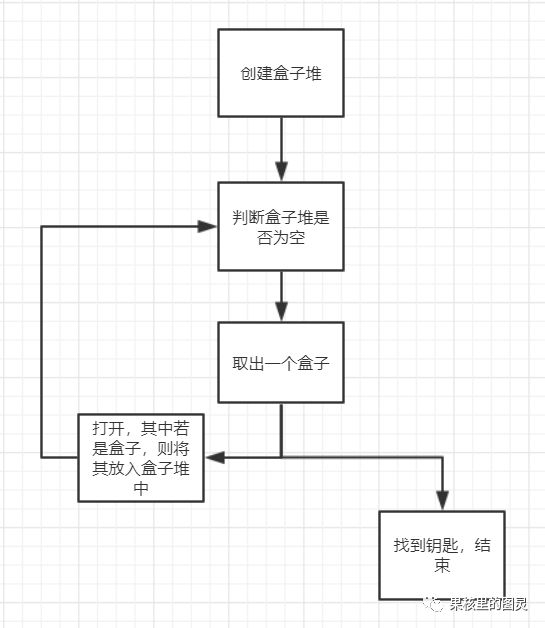
image.png
第二種
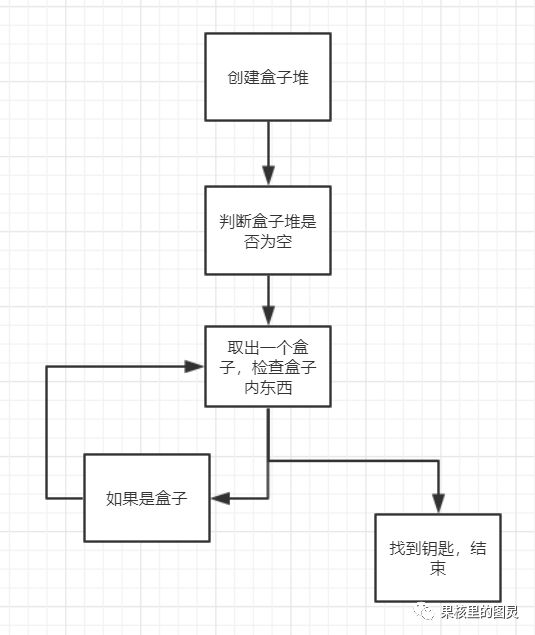
image.png
哪一種思路更加清晰呢?我們用代碼來實現一下:
第一種首先新建兩個類型盒子和鑰匙:
1class Box: 2 name=None 3 box=None 4 key=None 5 def __init__(self,name): 6 self.name=name 7 def set_box(self,box): 8 self.box=box 9 def set_key(self,key):10 self.key=key11class Key:12 name=None13 def __init__(self,name):14 self.name=name
查找算法:
1def look_for_key(box): 2 pile_box=box 3 i=0 4 while pile_box is not None: 5 #默認取出盒子堆中的第一個 6 handle_box=pile_box[0] 7 print("取出了:"+handle_box.name) 8 if handle_box.key is not None: 9 print("在"+handle_box.name+"中找到了鑰匙")10 return handle_box.key.name11 elif handle_box.box is not None:12 pile_box.append(handle_box.box)13 print("將"+handle_box.box.name+"放入盒子堆")14 pile_box.remove(handle_box)15 return "沒有找到鑰匙"
測試數據:
1if __name__ == '__main__': 2 #現在我創建一把鑰匙 3 key1=Key("我是鑰匙") 4 #現在我將鑰匙放在盒子1中 5 b1 = Box("1號盒子") 6 b1.set_key(key1) 7 # 創建多個盒子,互相放置 8 b2=Box("2號盒子") 9 b2.set_box(b1)10 b3=Box("3號盒子")11 b3.set_box(b2)12 b4=Box("4號盒子")13 b4.set_box(b3)14 b5=Box("5號盒子")15 #將這些盒子放入一個大盒子16 main_box=[b4,b5]17 print(look_for_key(main_box))
輸出:
1取出了:4號盒子 2將3號盒子放入盒子堆 3取出了:5號盒子 4取出了:3號盒子 5將2號盒子放入盒子堆 6取出了:2號盒子 7將1號盒子放入盒子堆 8取出了:1號盒子 9在1號盒子中找到了鑰匙10我是鑰匙
第二種(遞歸方式)
新建類型還是使用之前的,主要是重新寫一種查找算法:
1def look_for_key(box): 2 print("打開了"+box.name) 3 if box.key is not None: 4 print("在" + box.name + "中找到了鑰匙") 5 return 6 else: 7 look_for_key(box.box) 8if __name__ == '__main__': 9 #現在我創建一把鑰匙10 key1=Key("我是鑰匙")11 #現在我將鑰匙放在盒子1中12 b1 = Box("1號盒子")13 b1.set_key(key1)14 # 創建多個盒子,互相放置15 b2=Box("2號盒子")16 b2.set_box(b1)17 b3=Box("3號盒子")18 b3.set_box(b2)19 b4=Box("4號盒子")20 b4.set_box(b3)21 #將這些盒子放入一個大盒子22 main_box=Box("主盒子")23 main_box.set_box(b4)24 look_for_key(main_box)
輸出:
1打開了主盒子2打開了4號盒子3打開了3號盒子4打開了2號盒子5打開了1號盒子6在1號盒子中找到了鑰匙
總結以上兩種查找方式:使用循環可能使效率更高,使用遞歸使得代碼更易讀懂,如何選擇看哪一點對你更重要。
使用遞歸要注意基線條件和遞歸條件,否則很容易不小心陷入死循環。
快速排序
D&C
D&C(divide and conquer)分而治之是一種重要的解決問題思路。當面對問題束手無策時,我們應該考慮一下:分而治之可以解決嗎?
現在有一個問題,假如一塊土地(1680*640)需要均勻地分為正方形,而且正方形的邊長要盡量的大。該怎么分?
這個問題本質就是求兩條邊長的最大公因數。可以使用歐幾里得算法(輾轉相除)
1def func(num1,num2): 2 temp=0 3 while(num1%num2): 4 temp=num1%num2 5 num1=num2 6 num2=temp 7 return temp 8if __name__ == '__main__': 9 num1=168010 num2=64011 print(func(num1,num2))
快速排序
快速排序是一種常用的排序算法,比選擇排序快得多(O(n^2)),快速排序也使用了D&C。
選擇基準值
將數組分成兩個子數組:基準值左邊的數組和基準值右邊的數組
對這兩個數組進行快速排序
來寫一下代碼實現:
1def quicksort(list): 2 if len(list)<2: 3 ? ? ? ?return list 4 ? ?else: 5 ? ? ? ?#暫且取第一個值作為基準值 6 ? ? ? ?pivot=list[0] 7 ? ? ? ?less=[] 8 ? ? ? ?greater=[] 9 ? ? ? ?for item in list:10 ? ? ? ? ? ?if item
輸出結果:
1[2, 12, 43, 53, 542, 3253]
快速排序的最糟情況是O(n^2),O(n^2)已經很慢了,為什么還要叫它快速排序呢?
快速排序的平均運行時間為O(nlogn),而合并排序的時間總是O(nlogn),合并排序似乎更有優勢,那為什么不用合并排序呢?
因為大O表示法中的n是一個常量,當兩種算法的時間復雜度不一樣時,即使n在數值上不同,對總時間的影響很小,所以通常不考慮。
但有些時候,常量的影響很大,對快速排序和合并排序就是這樣,快速排序的常量小得多,所以當這兩種算法的時間復雜度都為O(nlogn)時,快速排序要快得多。而相較于最糟的情況,快速排序遇上平均情況的可能性更大,所以可以稍稍忽視這個問題。(快速排序最糟的情況下調用棧為O(n),在最佳情況下,調用棧長O(logn))
散列表
使用散列函數和數組可以構建散列表,散列表是包含額外邏輯的數據結構。
但是要編寫出完美的散列函數幾乎不可能,假如給兩個鍵分配的空間相同的話就會出現沖突。如何處理沖突呢?最簡單的辦法是:假如在某一空間上產生沖突,就在這一空間后再加上一個鏈表。但是假如這個鏈表很長,會很影響查找的速度(鏈表只能順序查找,查找時間為O(n))
所以一個能盡量避免沖突的散列函數是多么重要,那么怎么編寫一個性能較高的散列表呢?
較低的填裝因子(一旦填裝因子大于0.7,就需要調整長度)
良好的散列函數(讓數組中的值呈均勻分布,可以了解下SHA函數)
廣度優先搜索
廣度優先搜索能夠解決兩個問題:
兩個節點之間是否存在相連的路徑
最短的距離是多少?這個“最短距離”的含義有很多種。
想象這么一個問題:你想在你的微信好友和好友的好友中尋找是否有人是一名消防員,該如何查找?并且盡可能這人和你的關系更近些。
實現:
1from collections import deque 2def is_fireman(person): 3 #假設一個很簡單的判斷,假設消防員的名字尾部為f 4 return person[-1]=='f' 5def search_fireman(search_graph): 6 search_queue=deque() 7 search_queue+=search_graph["i"] 8 while search_queue: 9 person=search_queue.popleft()10 if is_fireman(person):11 return person12 else:13 if search_graph.__contains__(person):14 #假如這個人不是消防員,就將這個人的朋友全加入隊列15 search_queue+=search_graph[person]16 return "你的圈子里沒有消防員"17if __name__ == '__main__':18 test_graph={}19 test_graph["i"]=["Alice","Abby","Barry"]20 test_graph["Alice"]=["Bob","Tom"]21 test_graph["Abby"]=["Cart","Jay"]22 test_graph["Barry"]=["Welf","Zos"]23 print(search_fireman(test_graph))
輸出結果:
1Welf
迪克斯特拉算法
在圖中,搜索最小的“段”數可以用廣度優先算法,這就相當于默認每條邊的權重是相同的,如果每條邊的權重不同呢?那就需要用到迪克斯特拉算法。
概括來說,迪克斯特拉算法就是從起點開始,首先尋找最廉價的節點,更新其開銷并標記為已處理,然然后在未處理的節點中尋找開銷最小的節點,然后以此往復下去。
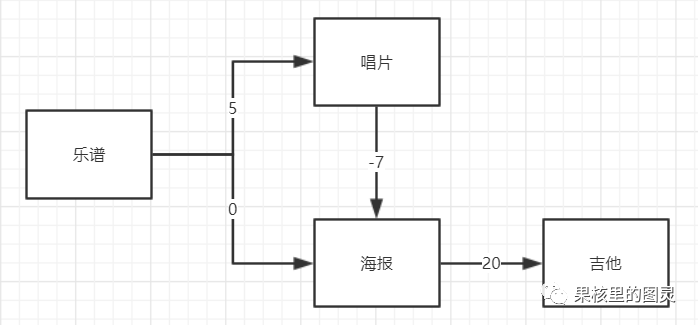
針對書中的這樣一個問題,我把題干提取出來:目標是用樂譜換鋼琴。現在樂譜可以免費換海報;海報加30元換吉他;海報加35元換架子鼓;樂譜加5元可以換唱片;唱片加15元換吉他;唱片加20元換架子鼓;吉他加20元換鋼琴;架子鼓加10元換鋼琴。
現在我用圖把這個關系表示出來:
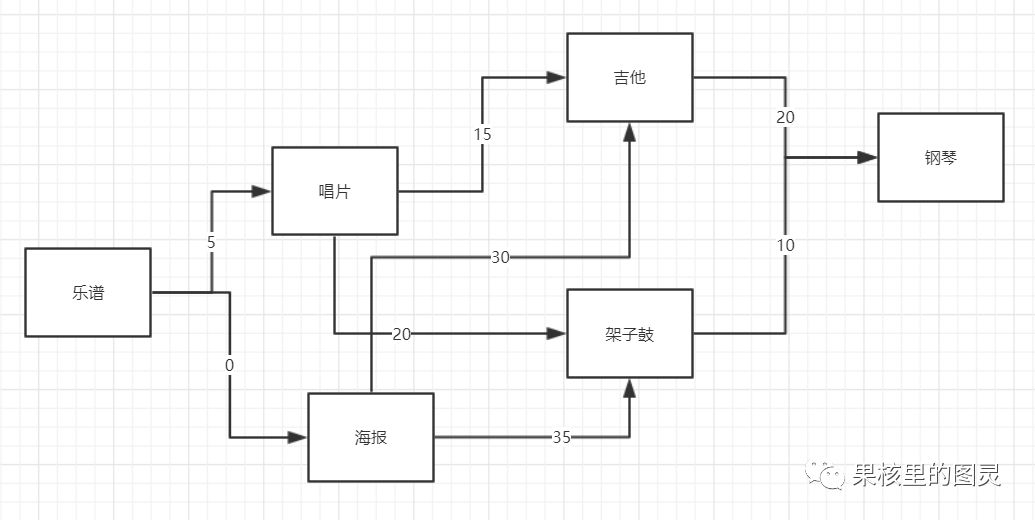
可以看出這是一個加權圖,現在我們要使用迪克斯特拉算法尋找最短路徑。
代碼實現:
1#檢索圖 2def dijkstra_find(costs,parent,processed): 3 #找到當前最廉價的節點 4 node =lowest_cost_node(costs,processed) 5 while node is not None: 6 cost=costs[node] 7 if not graph.__contains__(node): 8 break 9 neighbours=graph[node]10 for key in neighbours.keys():11 new_cost=cost+neighbours[key]12 if costs.__contains__(key):13 if costs[key] > new_cost:14 costs[key] = new_cost15 parent[key] = node16 else:17 costs[key]=new_cost18 parent[key] = node19 processed.append(node)20 node = lowest_cost_node(costs,processed)21#在開銷表中尋找最廉價的節點22def lowest_cost_node(costs,processed):23 lowest_cost=float("inf")24 lowest_node=None25 for node in costs:26 cost=costs[node]27 if cost
輸出:
最后的最低開銷表為:
父子節點表為:
可以看出,最優的交換的路徑為:piano-drum-record-music
最低開銷為:35元
貝爾曼-福德算法
在迪克特拉斯算法的基礎上,我們考慮這樣一種情況,假如邊的權重存在負值。
在迪克特拉斯算法中,我們首先尋找最廉價的節點,更新其開銷,再尋找未處理節點中最廉價的節點,以此往復。
可能出現這樣一個情況:
在將海報標記為已處理后,開始處理唱片,但是唱片到海報的路徑使得海報的開銷更小,又將更新海報的開銷,但是海報已經標記為已處理。那么就會出現一些問題。假如繼續使用迪克特拉斯算法,最后的結果肯定是錯的,大家可以更改參數試一下。為了正確解決問題,這時需要使用貝爾曼-福德算法。
貪心算法
對于一些比較復雜的問題,使用一些算法不能簡單有效地解決,這時候往往會使用貪心算法:每步操作都選擇局部最優解,最終得到的往往就是全局最優解。這似乎是想當然的做法,但是很多情況下真的行之有效。當然,貪心算法不適用于所有場景,但是他簡單高效。因為很多情況并不需要追求完美,只要能找到大致解決問題的辦法就行了。
假如我們面對這么一個問題:假設我開了一家網店,在全國各省都有生意,現在面臨發快遞的問題,假設現在的基礎物流不是很完善,每家快運公司只能覆蓋很少幾個省,那么我該如何在覆蓋全國34個省級行政區的情況下,選擇最少的快運公司?
這個問題看似不難,其實很復雜。
現在假設有n家快運公司,那么全部的組合有2^n種可能。
可以看到,假如有50家快遞公司,我將要考慮1125千億種可能。可以看到,沒有算法能很快的計算出這個問題,那么我們可以使用貪心算法,求局部最優解,然后將最終得到的視為全局最優解。
那么在這個問題下如何使用貪心算法?核心在于什么是局部最優條件?可以這樣:
選擇一家覆蓋了最多未覆蓋省的公司。
重復第一步。
我們在進行測試的時候稍稍簡化一下問題,將34個省改為10個省。代碼實現:
1def func(company,province): 2 result = set() 3 province_need=province 4 #當存在未覆蓋的省時,循環一直繼續 5 while province_need: 6 best_company=None 7 province_coverd=set() 8 #查找局部最好的選擇 9 for temp_company,temp_province in company.items():10 coverd=province_need & temp_province11 if len(coverd)>len(province_coverd):12 best_company=temp_company13 province_coverd=coverd14 province_need-=province_coverd15 result.add(best_company)16 return result17if __name__ == '__main__':18 province=set(["河北","山西","遼寧","吉林","黑龍江","江蘇","浙江","安徽","福建","江西"])19 company={}20 company["順豐"]=set(["河北","山西","遼寧","江蘇","浙江"])21 company["圓通"]=set(["吉林","浙江"])22 company["中通"]=set(["黑龍江","江西"])23 company["韻達"]=set(["江蘇","浙江","江蘇"])24 company["EMS"]=set(["浙江","安徽","河北","山西"])25 company["德邦"]=set(["福建","江西","安徽"])26 select_company=func(company,province)27 print(select_company)
輸出結果:
需要選擇這幾家快遞公司。
節點
開銷
海報
0
唱片
5
吉他
20
鼓
25
鋼琴
35
父節點
子節點
樂譜
唱片
樂譜
海報
唱片
吉他
唱片
鼓
鼓
鋼琴
N
2^N
10
1024
20
1048576
50
1125899906842624
-
算法
+關注
關注
23文章
4551瀏覽量
92014 -
python
+關注
關注
53文章
4752瀏覽量
84066 -
快速排序
+關注
關注
0文章
3瀏覽量
5421
原文標題:從一個騙局談生活中的基礎算法
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
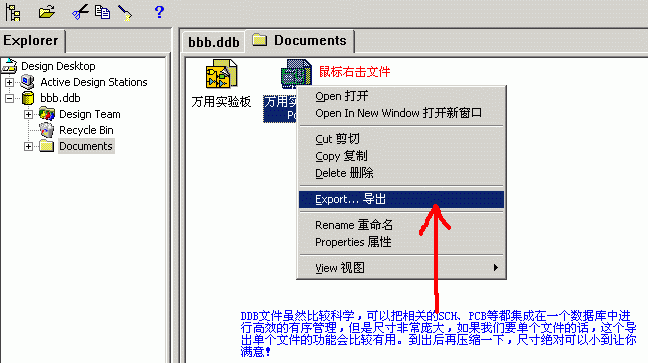
Protel在線教程:SCH的一些高級設置和常用技巧
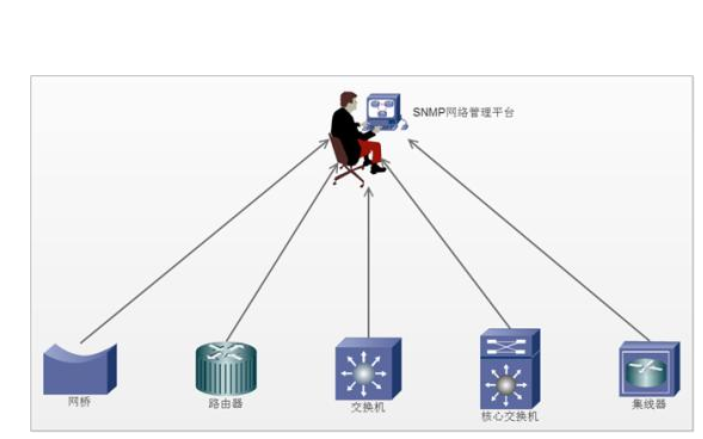
SNMP常用的一些OID詳細例表說明




 一些能夠解決生活中一些具體問題的常用算法的整理集合
一些能夠解決生活中一些具體問題的常用算法的整理集合










評論