這篇文章中我們來探討一下常用的非比較排序算法:計數排序,基數排序,桶排序。在一定條件下,它們的時間復雜度可以達到O(n)。
這里我們用到的唯一數據結構就是數組,當然我們也可以利用鏈表來實現下述算法。
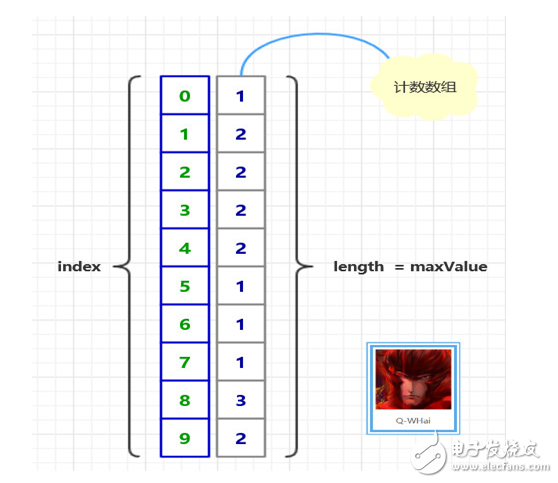
計數排序用到一個額外的計數數組C,根據數組C來將原數組A中的元素排到正確的位置。
通俗地理解,例如有10個年齡不同的人,假如統計出有8個人的年齡不比小明大(即小于等于小明的年齡,這里也包括了小明),那么小明的年齡就排在第8位,通過這種思想可以確定每個人的位置,也就排好了序。當然,年齡一樣時需要特殊處理(保證穩定性):通過反向填充目標數組,填充完畢后將對應的數字統計遞減,可以確保計數排序的穩定性。
計數排序的步驟如下:
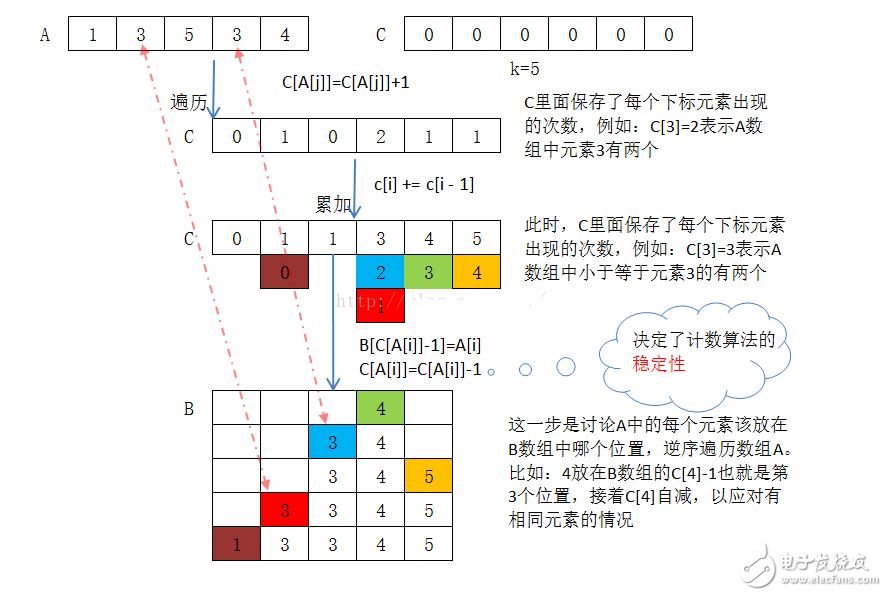
統計數組A中每個值A[i]出現的次數,存入C[A[i]]
從前向后,使數組C中的每個值等于其與前一項相加,這樣數組C[A[i]]就變成了代表數組A中小于等于A[i]的元素個數
反向填充目標數組B:將數組元素A[i]放在數組B的第C[A[i]]個位置(下標為C[A[i]] – 1),每放一個元素就將C[A[i]]遞減
計數排序的實現代碼如下:
#include
usingnamespacestd;
// 分類 ------------ 內部非比較排序
// 數據結構 --------- 數組
// 最差時間復雜度 ---- O(n + k)
// 最優時間復雜度 ---- O(n + k)
// 平均時間復雜度 ---- O(n + k)
// 所需輔助空間 ------ O(n + k)
// 穩定性 ----------- 穩定
constintk=100;// 基數為100,排序[0,99]內的整數
intC[k];// 計數數組
voidCountingSort(intA[],intn)
{
for(inti=0;i
{
C[i]=0;
}
for(inti=0;i
{
C[A[i]]++;
}
for(inti=1;i
{
C[i]=C[i]+C[i-1];
}
int*B=(int*)malloc((n)*sizeof(int));// 分配臨時空間,長度為n,用來暫存中間數據
for(inti=n-1;i>=0;i--)// 從后向前掃描保證計數排序的穩定性(重復元素相對次序不變)
{
B[--C[A[i]]]=A[i];// 把每個元素A[i]放到它在輸出數組B中的正確位置上
// 當再遇到重復元素時會被放在當前元素的前一個位置上保證計數排序的穩定性
}
for(inti=0;i
{
A[i]=B[i];
}
free(B);// 釋放臨時空間
}
intmain()
{
intA[]={15,22,19,46,27,73,1,19,8};// 針對計數排序設計的輸入,每一個元素都在[0,100]上且有重復元素
intn=sizeof(A)/sizeof(int);
CountingSort(A,n);
printf("計數排序結果:");
for(inti=0;i
{
printf("%d ",A[i]);
}
printf("\n");
return0;
}
下圖給出了對{ 4, 1, 3, 4, 3 }進行計數排序的簡單演示過程
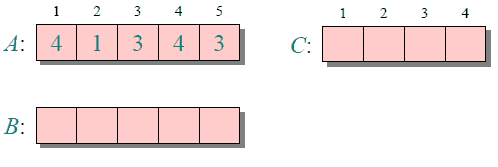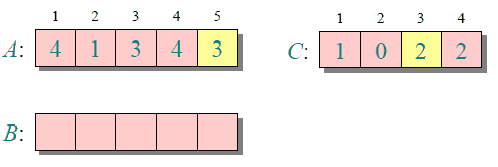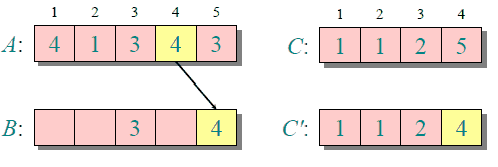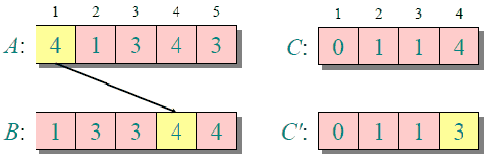
計數排序的時間復雜度和空間復雜度與數組A的數據范圍(A中元素的最大值與最小值的差加上1)有關,因此對于數據范圍很大的數組,計數排序需要大量時間和內存。
例如:對0到99之間的數字進行排序,計數排序是最好的算法,然而計數排序并不適合按字母順序排序人名,將計數排序用在基數排序算法中,能夠更有效的排序數據范圍很大的數組。
基數排序(Radix Sort)
基數排序的發明可以追溯到1887年赫爾曼·何樂禮在打孔卡片制表機上的貢獻。它是這樣實現的:將所有待比較正整數統一為同樣的數位長度,數位較短的數前面補零。然后,從最低位開始進行基數為10的計數排序,一直到最高位計數排序完后,數列就變成一個有序序列(利用了計數排序的穩定性)。
基數排序的實現代碼如下:
#include
usingnamespacestd;
// 分類 ------------- 內部非比較排序
// 數據結構 ---------- 數組
// 最差時間復雜度 ---- O(n * dn)
// 最優時間復雜度 ---- O(n * dn)
// 平均時間復雜度 ---- O(n * dn)
// 所需輔助空間 ------ O(n * dn)
// 穩定性 ----------- 穩定
constintdn=3;// 待排序的元素為三位數及以下
constintk=10;// 基數為10,每一位的數字都是[0,9]內的整數
intC[k];
intGetDigit(intx,intd)// 獲得元素x的第d位數字
{
intradix[]={1,1,10,100};// 最大為三位數,所以這里只要到百位就滿足了
return(x/radix[d])%10;
}
voidCountingSort(intA[],intn,intd)// 依據元素的第d位數字,對A數組進行計數排序
{
for(inti=0;i
{
C[i]=0;
}
for(inti=0;i
{
C[GetDigit(A[i],d)]++;
}
for(inti=1;i
{
C[i]=C[i]+C[i-1];
}
int*B=(int*)malloc(n *sizeof(int));
for(inti=n-1;i>=0;i--)
{
intdight=GetDigit(A[i],d);// 元素A[i]當前位數字為dight
B[--C[dight]]=A[i];// 根據當前位數字,把每個元素A[i]放到它在輸出數組B中的正確位置上
// 當再遇到當前位數字同為dight的元素時,會將其放在當前元素的前一個位置上保證計數排序的穩定性
}
for(inti=0;i
{
A[i]=B[i];
}
free(B);
}
voidLsdRadixSort(intA[],intn)// 最低位優先基數排序
{
for(intd=1;d<=?dn;d++)?????// 從低位到高位
CountingSort(A,n,d);// 依據第d位數字對A進行計數排序
}
intmain()
{
intA[]={20,90,64,289,998,365,852,123,789,456};// 針對基數排序設計的輸入
intn=sizeof(A)/sizeof(int);
LsdRadixSort(A,n);
printf("基數排序結果:");
for(inti=0;i
{
printf("%d ",A[i]);
}
printf("\n");
return0;
}
下圖給出了對{ 329, 457, 657, 839, 436, 720, 355 }進行基數排序的簡單演示過程
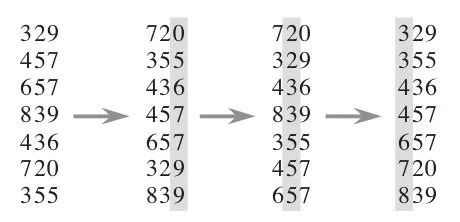
基數排序的時間復雜度是O(n*dn),其中n是待排序元素個數,dn是數字位數。這個時間復雜度不一定優于O(n log n),dn的大小取決于數字位的選擇(比如比特位數),和待排序數據所屬數據類型的全集的大小;dn決定了進行多少輪處理,而n是每輪處理的操作數目。
如果考慮和比較排序進行對照,基數排序的形式復雜度雖然不一定更小,但由于不進行比較,因此其基本操作的代價較小,而且如果適當的選擇基數,dn一般不大于log n,所以基數排序一般要快過基于比較的排序,比如快速排序。由于整數也可以表達字符串(比如名字或日期)和特定格式的浮點數,所以基數排序并不是只能用于整數排序。
桶排序(Bucket Sort)
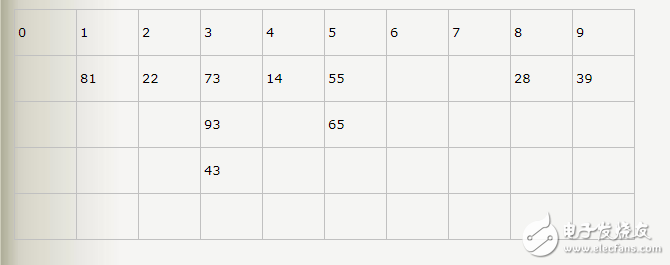
桶排序也叫箱排序。工作的原理是將數組元素映射到有限數量個桶里,利用計數排序可以定位桶的邊界,每個桶再各自進行桶內排序(使用其它排序算法或以遞歸方式繼續使用桶排序)。
桶排序的實現代碼如下:
#include
usingnamespacestd;
// 分類 ------------- 內部非比較排序
// 數據結構 --------- 數組
// 最差時間復雜度 ---- O(nlogn)或O(n^2),只有一個桶,取決于桶內排序方式
// 最優時間復雜度 ---- O(n),每個元素占一個桶
// 平均時間復雜度 ---- O(n),保證各個桶內元素個數均勻即可
// 所需輔助空間 ------ O(n + bn)
// 穩定性 ----------- 穩定
/* 本程序用數組模擬桶 */
constintbn=5;// 這里排序[0,49]的元素,使用5個桶就夠了,也可以根據輸入動態確定桶的數量
intC[bn];// 計數數組,存放桶的邊界信息
voidInsertionSort(intA[],intleft,intright)
{
for(inti=left+1;i<=?right;i++)??// 從第二張牌開始抓,直到最后一張牌
{
intget=A[i];
intj=i-1;
while(j>=left&&A[j]>get)
{
A[j+1]=A[j];
j--;
}
A[j+1]=get;
}
}
intMapToBucket(intx)
{
returnx/10;// 映射函數f(x),作用相當于快排中的Partition,把大量數據分割成基本有序的數據塊
}
voidCountingSort(intA[],intn)
{
for(inti=0;i
{
C[i]=0;
}
for(inti=0;i
{
C[MapToBucket(A[i])]++;
}
for(inti=1;i
{
C[i]=C[i]+C[i-1];
}
int*B=(int*)malloc((n)*sizeof(int));
for(inti=n-1;i>=0;i--)// 從后向前掃描保證計數排序的穩定性(重復元素相對次序不變)
{
intb=MapToBucket(A[i]);// 元素A[i]位于b號桶
B[--C[b]]=A[i];// 把每個元素A[i]放到它在輸出數組B中的正確位置上
// 桶的邊界被更新:C[b]為b號桶第一個元素的位置
}
for(inti=0;i
{
A[i]=B[i];
}
free(B);
}
voidBucketSort(intA[],intn)
{
CountingSort(A,n);// 利用計數排序確定各個桶的邊界(分桶)
for(inti=0;i
{
intleft=C[i];// C[i]為i號桶第一個元素的位置
intright=(i==bn-1?n-1:C[i+1]-1);// C[i+1]-1為i號桶最后一個元素的位置
if(left
InsertionSort(A,left,right);
}
}
intmain()
{
intA[]={29,25,3,49,9,37,21,43};// 針對桶排序設計的輸入
intn=sizeof(A)/sizeof(int);
BucketSort(A,n);
printf("桶排序結果:");
for(inti=0;i
{
printf("%d ",A[i]);
}
printf("\n");
return0;
}
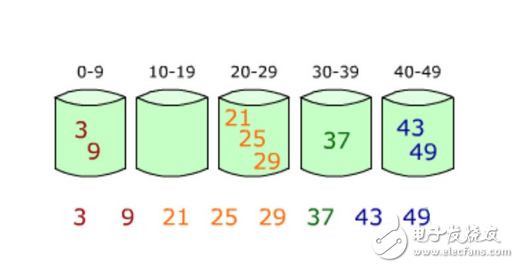
下圖給出了對{ 29, 25, 3, 49, 9, 37, 21, 43 }進行桶排序的簡單演示過程
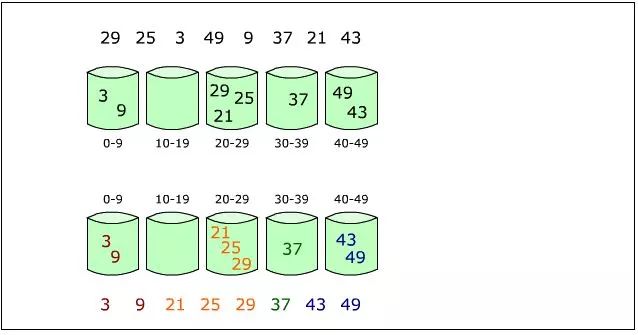
桶排序不是比較排序,不受到O(nlogn)下限的影響,它是鴿巢排序的一種歸納結果,當所要排序的數組值分散均勻的時候,桶排序擁有線性的時間復雜度。
-
數據結構
+關注
關注
3文章
573瀏覽量
40092 -
排序算法
+關注
關注
0文章
52瀏覽量
10051 -
數組
+關注
關注
1文章
415瀏覽量
25908
原文標題:常用排序算法總結(2)
文章出處:【微信號:LinuxHub,微信公眾號:Linux愛好者】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
資料下載:基數排序:*** 與 MSD
C語言實現簡單的基數排序




 常用的非比較排序算法:計數排序,基數排序,桶排序的詳細資料概述
常用的非比較排序算法:計數排序,基數排序,桶排序的詳細資料概述











評論