▌一. 前言:
作為AI入門小白,參考了一些文章,想記點筆記加深印象,發出來是給有需求的童鞋學習共勉,大神輕拍!
【毒雞湯】:算法這東西,讀完之后的狀態多半是 -->“我是誰,我在哪?”沒事的,吭哧吭哧學總能學會,畢竟還有千千萬萬個算法等著你。
本文貨很干,堪比沙哈拉大沙漠,自己挑的文章,含著淚也要讀完!
▌二. 科普:
生物上的神經元就是接收四面八方的刺激(輸入),然后做出反應(輸出),給它一點??就燦爛。
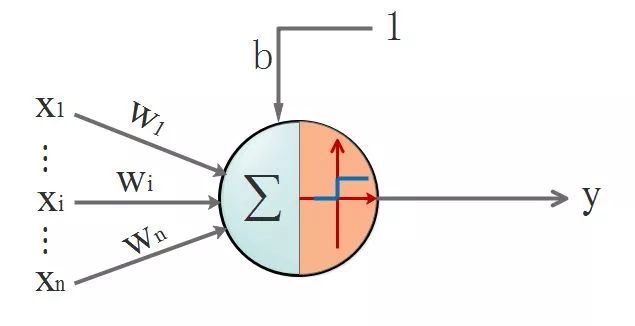
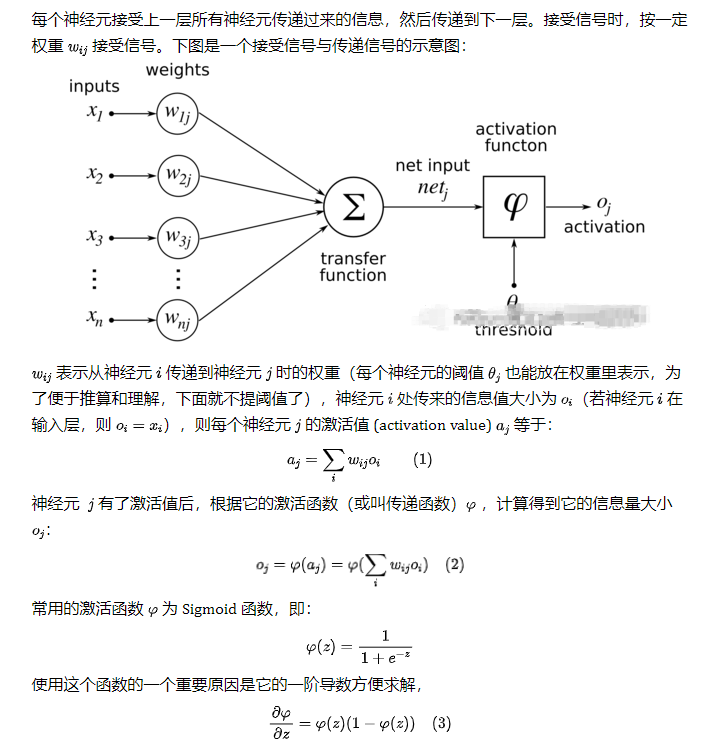
仿生嘛,于是喜歡放飛自我的某些人就提出了人工神經網絡。一切的基礎-->人工神經單元,看圖:
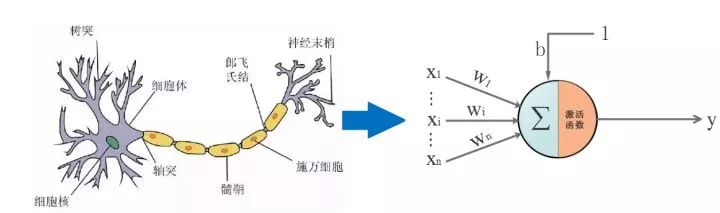
▌三. 通往沙漠的入口: 神經元是什么,有什么用:
開始前,需要搞清楚一個很重要的問題:人工神經網絡里的神經元是什么,有什么用。只有弄清楚這個問題,你才知道你在哪里,在做什么,要往哪里去。
首先,回顧一下神經元的結構,看下圖, 我們先忽略激活函數不管:
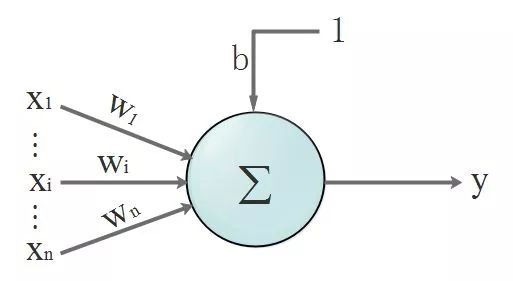

沒錯,開始曬公式了!我們的數據都是離散的,為了看得更清楚點,所以換個表達方式,把離散的數據寫成向量。該不會忘了向量是啥吧?回頭致電問候一下當年的體育老師!

現在回答問題剛才的問題:
一個神經元是什么:參照式(1.6),從函數圖像角度看,這就是一根直線。
一個神經元有什么用:要說明用途就要給出一個應用場景:分類。一個神經元就是一條直線,相當于楚河漢界,可以把紅棋綠棋分隔開,此時它就是個分類器。所以,在線性場景下,單個神經元能達到分類的作用,它總能學習到一條合適的直線,將兩類元素區分出來。
先睹為快,看效果圖,自己可以去玩:傳送門
http://t.cn/RBCoWof
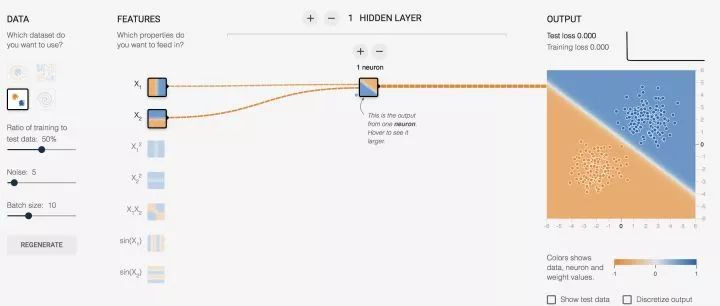
對上面的圖簡單說明一下:
(x1,x2) 對于神經元的輸入都是 x, 而對我們而言,這數據就是意義上的點的坐標,我們習慣寫成 (x,y)。
又要劃重點了:
我們需要對神經元的輸出做判定,那么就需要有判定規則,通過判定規則后我們才能拿到我們想要的結果,這個規則就是:
假設,0代表紅點,1代表藍點(這些數據都是事先標定好的,在監督學習下,神經元會知道點是什么顏色并以這個已知結果作為標桿進行學習)
當神經元輸出小于等于 0 時,最終結果輸出為 0,這是個紅點
當神經元輸出大于 1 時,最終結果輸出為 1,這是個藍點
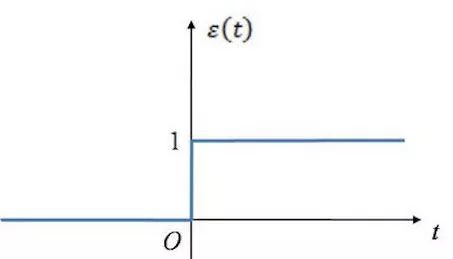
上面提到的規則讓我聞到了激活函數的味道!(這里只是線性場景,雖然不合適,但是簡單起見,使用了單位階躍函數來描述激活函數的功能)當 x<=0 時,y = 0; 當 x > 0 時,y = 1
這是階躍函數的長相:
此時神經元的長相:
▌四. 茫茫大漠第一步: 激活函數是什么,有什么用
從上面的例子,其實已經說明了激活函數的作用;但是,我們通常面臨的問題,不是簡單的線性問題,不能用單位階躍函數作為激活函數,原因是:
階躍函數在x=0時不連續,即不可導,在非0處導數為0。用人話說就是它具備輸出限定在[0-1],但是它不具備絲滑的特性,這個特性很重要。并且在非0處導數為0,也就是硬飽和,壓根兒就沒梯度可言,梯度也很重要,梯度意味著在神經元傳播間是有反應的,而不是“死”了的。
接下來說明下,激活函數所具備的特性有什么,只挑重要的幾點特性講:
非線性:即導數不是常數,不然就退化成直線。對于一些畫一條直線仍然無法分開的問題,非線性可以把直線掰彎,自從變彎以后,就能包羅萬象了。
幾乎處處可導:也就是具備“絲滑的特性”,不要應激過度,要做正常人。數學上,處處可導為后面降到的后向傳播算法(BP算法)提供了核心條件
輸出范圍有限:一般是限定在[0,1],有限的輸出范圍使得神經元對于一些比較大的輸入也會比較穩定。
非飽和性:飽和就是指,當輸入比較大的時候,輸出幾乎沒變化了,那么會導致梯度消失!什么是梯度消失:就是你天天給女生送花,一開始妹紙還驚喜,到后來直接麻木沒反應了。梯度消失帶來的負面影響就是會限制了神經網絡表達能力,詞窮的感覺你有過么。sigmod,tanh函數都是軟飽和的,階躍函數是硬飽和。軟是指輸入趨于無窮大的時候輸出無限接近上線,硬是指像階躍函數那樣,輸入非0輸出就已經始終都是上限值。數學表示我就懶得寫了,傳送門在此(https://www.cnblogs.com/rgvb178/p/6055213.html),里面有寫到。如果激活函數是飽和的,帶來的缺陷就是系統迭代更新變慢,系統收斂就慢,當然這是可以有辦法彌補的,一種方法是使用交叉熵函數作為損失函數,這里不多說。ReLU是非飽和的,親測效果挺不錯,所以這貨最近挺火的。
單調性:即導數符號不變。導出要么一直大于0,要么一直小于0,不要上躥下跳。導數符號不變,讓神經網絡訓練容易收斂。
這里只說我們用到的激活函數:
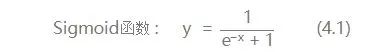
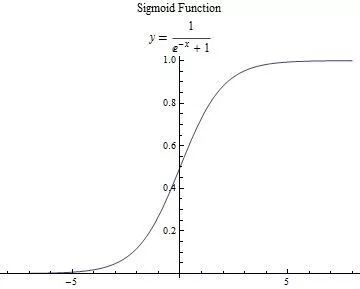
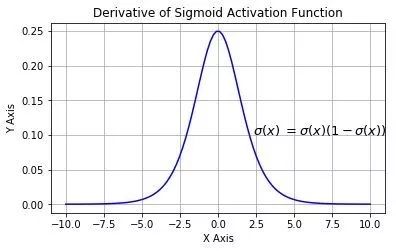
求一下它的導數把,因為后面講bp算法會直接套用它:
先祭出大殺器,高中數學之復合函數求導法則:

它的導數圖像:
▌五. 沙漠中心的風暴:BP(Back Propagation)算法
1. 神經網絡的結構
經過上面的介紹,單個神經元不足以讓人心動,唯有組成網絡。神經網絡是一種分層結構,一般由輸入曾,隱藏層,輸出層組成。所以神經網絡至少有3層,隱藏層多于1,總層數大于3的就是我們所說的深度學習了。
輸入層:就是接收原始數據,然后往隱層送
輸出層:神經網絡的決策輸出
隱藏層:該層可以說是神經網絡的關鍵,相當于對數據做一次特征提取。隱藏層的意義,是把前一層的向量變成新的向量。就是坐標變換,說人話就是把數據做平移,旋轉,伸縮,扭曲,讓數據變得線性可分。可能這個不那么好理解,舉個栗子:
下面的圖左側是原始數據,中間很多綠點,外圍是很多紅點,如果你是神經網絡,你會怎么做呢?
一種做法:把左圖的平面看成一塊布,把它縫合成一個閉合的包包(相當于數據變換到了一個3維坐標空間),然后把有綠色點的部分擼到頂部(伸縮和扭曲),然后外圍的紅色點自然在另一端了,要是姿勢還不夠帥,就挪挪位置(平移)。這時候干脆利落的砍一刀,綠點紅點就徹底區分開了。
重要的東西再說一遍:神經網絡換著坐標空間玩數據,根據需要,可降維,可升維,可大,可小,可圓可扁,就是這么“無敵”
這個也可以自己去玩玩,直觀的感受一下:傳送門
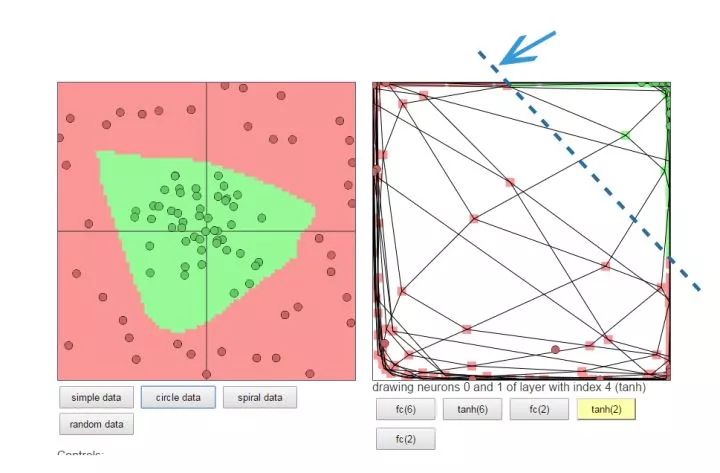
2.正反向傳播過程
看圖,這是一個典型的三層神經網絡結構,第一層是輸入層,第二層是隱藏層,第三層是輸出層。PS:不同的應用場景,神經網絡的結構要有針對性的設計,這里僅僅是為了推導算法和計算方便才采用這個簡單的結構
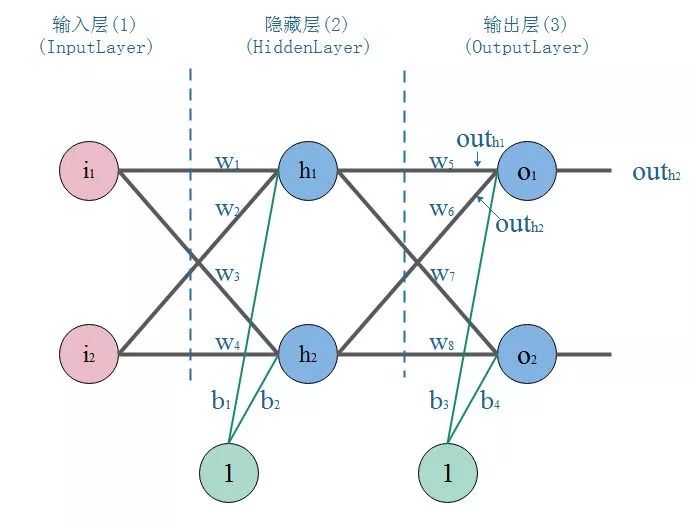
我們以戰士打靶,目標是訓練戰士能命中靶心成為神槍手作為場景:
那么我們手里有這樣一些數據:一堆槍擺放的位置(x,y),以及射擊結果,命中靶心和不命中靶心。
我們的目標是:訓練出一個神經網絡模型,輸入一個點的坐標(射擊姿勢),它就告訴你這個點是什么結果(是否命中)。
我們的方法是:訓練一個能根據誤差不斷自我調整的模型,訓練模型的步驟是:
正向傳播:把點的坐標數據輸入神經網絡,然后開始一層一層的傳播下去,直到輸出層輸出結果。
反向傳播(BP):就好比戰士去靶場打靶,槍的擺放位置(輸入),和靶心(期望的輸出)是已知。戰士(神經網絡)一開始的時候是這樣做的,隨便開一槍(w,b參數初始化稱隨機值),觀察結果(這時候相當于進行了一次正向傳播)。然后發現,偏離靶心左邊,應該往右點兒打。所以戰士開始根據偏離靶心的距離(誤差,也稱損失)調整了射擊方向往右一點(這時,完成了一次反向傳播)
當完成了一次正反向傳播,也就完成了一次神經網絡的訓練迭代,反復調整射擊角度(反復迭代),誤差越來越小,戰士打得越來越準,神槍手模型也就誕生了。
3.BP算法推導和計算
參數初始化:

正向傳播:

2.隱層-->輸出層:

正向傳播結束,我們看看輸出層的輸出結果:[0.7987314002, 0.8374488853],但是我們希望它能輸出[0.01, 0.99],所以明顯的差太遠了,這個時候我們就需要利用反向傳播,更新權值w,然后重新計算輸出.
反向傳播:
1.計算輸出誤差:

PS: 這里我要說的是,用這個作為誤差的計算,因為它簡單,實際上用的時候效果不咋滴。如果激活函數是飽和的,帶來的缺陷就是系統迭代更新變慢,系統收斂就慢,當然這是可以有辦法彌補的,一種方法是使用交叉熵函數作為損失函數。
交叉熵做為代價函數能達到上面說的優化系統收斂下歐工,是因為它在計算誤差對輸入的梯度時,抵消掉了激活函數的導數項,從而避免了因為激活函數的“飽和性”給系統帶來的負面影響。如果項了解更詳細的證明可以點 -->傳送門(https://blog.csdn.net/lanchunhui/article/details/50086025)
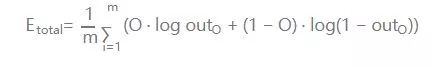
對輸出的偏導數:
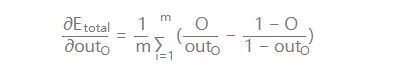
2.隱層-->輸出層的權值及偏置b的更新:
先放出鏈式求導法則:

以更新w5舉例:
我們知道,權重w的大小能直接影響輸出,w不合適那么會使得輸出誤差。要想直到某一個w值對誤差影響的程度,可以用誤差對該w的變化率來表達。如果w的一點點變動,就會導致誤差增大很多,說明這個w對誤差影響的程度就更大,也就是說,誤差對該w的變化率越高。而誤差對w的變化率就是誤差對w的偏導。
所以,看下圖,總誤差的大小首先受輸出層神經元O1的輸出影響,繼續反推,O1的輸出受它自己的輸入的影響,而它自己的輸入會受到w5的影響。這就是連鎖反應,從結果找根因。
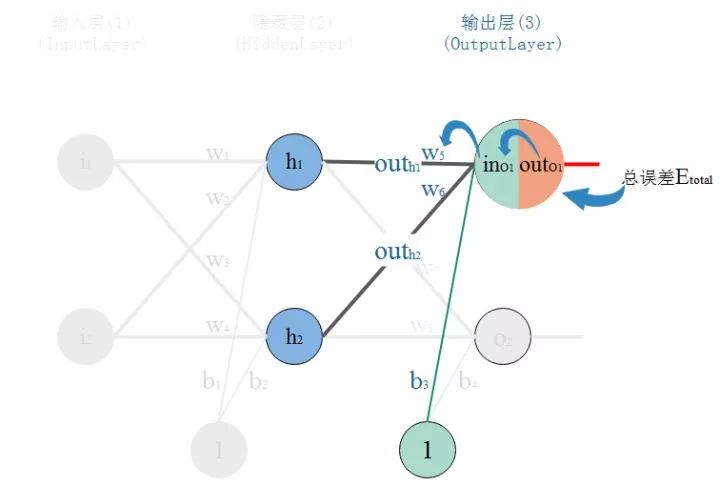
那么,根據鏈式法則則有:
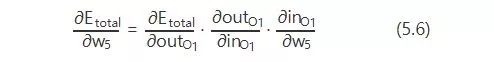
現在挨個計算:


有個學習率的東西,學習率取個0.5。關于學習率,不能過高也不能過低。因為訓練神經網絡系統的過程,就是通過不斷的迭代,找到讓系統輸出誤差最小的參數的過程。每一次迭代都經過反向傳播進行梯度下降,然而誤差空間不是一個滑梯,一降到底,常規情況下就像坑洼的山地。學習率太小,那就很容易陷入局部最優,就是你認為的最低點并不是整個空間的最低點。如果學習率太高,那系統可能難以收斂,會在一個地方上串下跳,無法對準目標(目標是指誤差空間的最低點),可以看圖:
xy軸是權值w平面,z軸是輸出總誤差。整個誤差曲面可以看到兩個明顯的低點,顯然右邊最低,屬于全局最優。而左邊的是次低,從局部范圍看,屬于局部最優。而圖中,在給定初始點的情況下,標出的兩條抵達低點的路線,已經是很理想情況的梯度下降路徑。
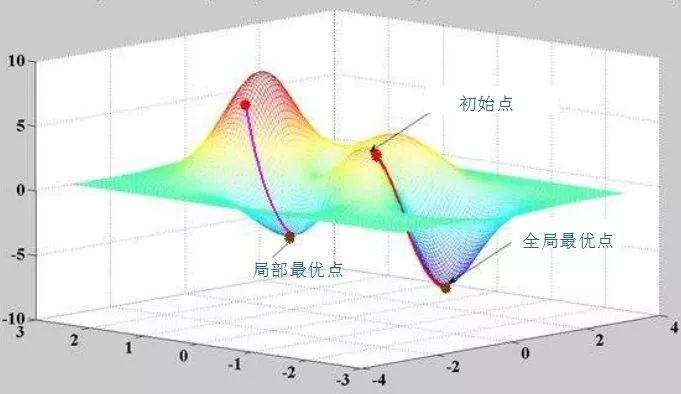

3.輸入層-->隱層的權值及偏置b更新:
以更新w1為例:仔細觀察,我們在求w5的更新,誤差反向傳遞路徑輸出層-->隱層,即out(O1)-->in(O1)-->w5,總誤差只有一根線能傳回來。但是求w1時,誤差反向傳遞路徑是隱藏層-->輸入層,但是隱藏層的神經元是有2根線的,所以總誤差沿著2個路徑回來,也就是說,計算偏導時,要分開來算。看圖:
那么,現在開始算總誤差對w1的偏導:





4.結論:
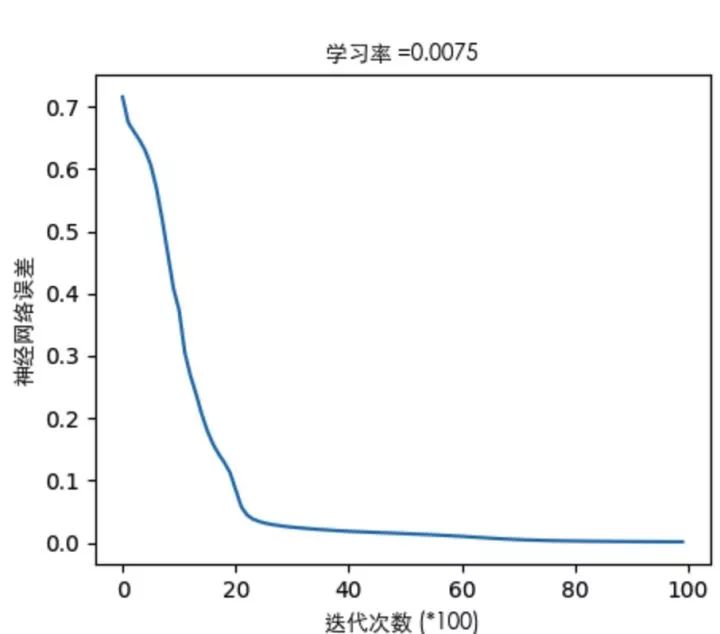
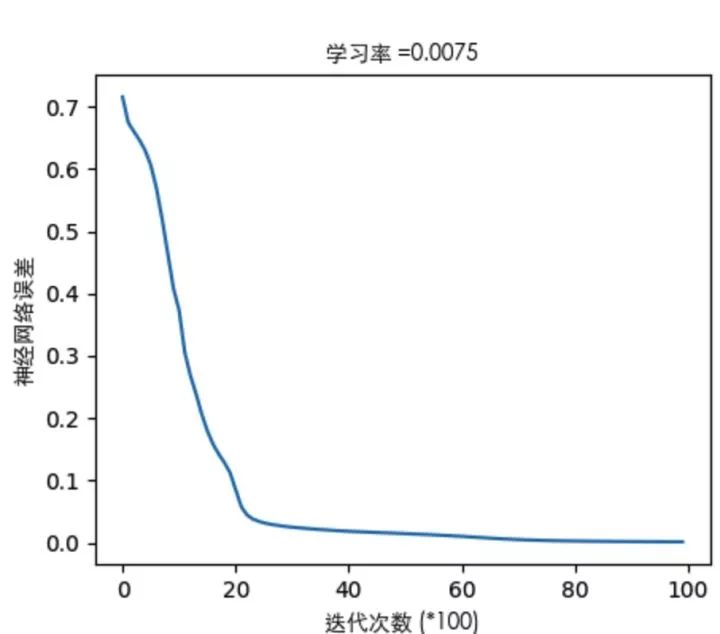
我們通過親力親為的計算,走過了正向傳播,也體會了反向傳播,完成了一次訓練(迭代)。隨著迭代加深,輸出層的誤差會越來越小,專業點說就是系統趨于收斂。來一張系統誤差隨迭代次數變化的圖來表明我剛才說描述:
▌六. 沙漠的綠洲:代碼實現
1. 代碼代碼!
其實已經有很多機器學習的框架可以很簡單的實現神經網絡。但是我們的目標是:在看懂算法之后,我們是否能照著算法的整個過程,去實現一遍,可以加深對算法原理的理解,以及對算法實現思路的的理解。順便說打個call,numpy這個庫,你值得擁有!
代碼實現如下。代碼里已經做了盡量啰嗦的注釋,關鍵實現的地方對標了公式的編號,如果看的不明白的地方多回來啃一下算法推導。對應代碼也傳到了github上。
代碼能自己定義神經網絡的結構,支持深度網絡。代碼實現了對紅藍顏色的點做分類的模型訓練,通過3層網絡結構,改變隱藏層的神經元個數,通過圖形顯示隱藏層神經元數量對問題的解釋能力。
代碼中還實現了不同激活函數。隱藏層可以根據需要換著激活函數玩,輸出層一般就用sigmoid,當然想換也隨你喜歡~
#coding:utf-8importh5pyimportsklearn.datasetsimportsklearn.linear_modelimportmatplotlibimportmatplotlib.font_managerasfmimportmatplotlib.pyplotaspltimportnumpyasnpnp.random.seed(1)font=fm.FontProperties(fname='/System/Library/Fonts/STHeitiLight.ttc')matplotlib.rcParams['figure.figsize']=(10.0,8.0)defsigmoid(input_sum):"""函數:激活函數Sigmoid輸入:input_sum:輸入,即神經元的加權和返回:output:激活后的輸出input_sum:把輸入緩存起來返回"""output=1.0/(1+np.exp(-input_sum))returnoutput,input_sumdefsigmoid_back_propagation(derror_wrt_output,input_sum):"""函數:誤差關于神經元輸入的偏導:dE/dIn=dE/dOut*dOut/dIn參照式(5.6)其中:dOut/dIn就是激活函數的導數dy=y(1-y),見式(5.9)dE/dOut誤差對神經元輸出的偏導,見式(5.8)輸入:derror_wrt_output:誤差關于神經元輸出的偏導:dE/dy?=1/2(d(expect_to_output-output)**2/doutput)=-(expect_to_output-output)input_sum:輸入加權和返回:derror_wrt_dinputs:誤差關于輸入的偏導,見式(5.13)"""output=1.0/(1+np.exp(-input_sum))doutput_wrt_dinput=output*(1-output)derror_wrt_dinput=derror_wrt_output*doutput_wrt_dinputreturnderror_wrt_dinputdefrelu(input_sum):"""函數:激活函數ReLU輸入:input_sum:輸入,即神經元的加權和返回:outputs:激活后的輸出input_sum:把輸入緩存起來返回"""output=np.maximum(0,input_sum)returnoutput,input_sumdefrelu_back_propagation(derror_wrt_output,input_sum):"""函數:誤差關于神經元輸入的偏導:dE/dIn=dE/dOut*dOut/dIn其中:dOut/dIn就是激活函數的導數dE/dOut誤差對神經元輸出的偏導輸入:derror_wrt_output:誤差關于神經元輸出的偏導input_sum:輸入加權和返回:derror_wrt_dinputs:誤差關于輸入的偏導"""derror_wrt_dinputs=np.array(derror_wrt_output,copy=True)derror_wrt_dinputs[input_sum<=?0]?=?0????return?derror_wrt_dinputsdef?tanh(input_sum):????"""????函數:????????激活函數?tanh????輸入:????????input_sum:?輸入,即神經元的加權和????返回:????????output:?激活后的輸出????????input_sum:?把輸入緩存起來返回????"""????output?=?np.tanh(input_sum)????return?output,?input_sumdef?tanh_back_propagation(derror_wrt_output,?input_sum):????"""????函數:????????誤差關于神經元輸入的偏導:?dE/dIn?=?dE/dOut?*?dOut/dIn????????其中:?dOut/dIn?就是激活函數的導數?tanh'(x)?=?1?-?x2??????????????dE/dOut?誤差對神經元輸出的偏導????輸入:????????derror_wrt_output:誤差關于神經元輸出的偏導:?dE/dy??=?1/2(d(expect_to_output?-?output)**2/doutput)?=?-(expect_to_output?-?output)????????input_sum:?輸入加權和????返回:????????derror_wrt_dinputs:?誤差關于輸入的偏導????"""????output?=?np.tanh(input_sum)????doutput_wrt_dinput?=?1?-?np.power(output,?2)????derror_wrt_dinput?=??derror_wrt_output?*?doutput_wrt_dinput????return?derror_wrt_dinputdef?activated(activation_choose,?input):????"""把正向激活包裝一下"""????if?activation_choose?==?"sigmoid":????????return?sigmoid(input)????elif?activation_choose?==?"relu":????????return?relu(input)????elif?activation_choose?==?"tanh":????????return?tanh(input)????return?sigmoid(input)def?activated_back_propagation(activation_choose,?derror_wrt_output,?output):????"""包裝反向激活傳播"""????if?activation_choose?==?"sigmoid":????????return?sigmoid_back_propagation(derror_wrt_output,?output)????elif?activation_choose?==?"relu":????????return?relu_back_propagation(derror_wrt_output,?output)????elif?activation_choose?==?"tanh":????????return?tanh_back_propagation(derror_wrt_output,?output)????return?sigmoid_back_propagation(derror_wrt_output,?output)class?NeuralNetwork:????def?__init__(self,?layers_strcuture,?print_cost?=?False):????????self.layers_strcuture?=?layers_strcuture????????self.layers_num?=?len(layers_strcuture)????????#?除掉輸入層的網絡層數,因為其他層才是真正的神經元層????????self.param_layers_num?=?self.layers_num?-?1????????self.learning_rate?=?0.0618????????self.num_iterations?=?2000????????self.x?=?None????????self.y?=?None????????self.w?=?dict()????????self.b?=?dict()????????self.costs?=?[]????????self.print_cost?=?print_cost????????self.init_w_and_b()????def?set_learning_rate(self,?learning_rate):????????"""設置學習率"""????????self.learning_rate?=?learning_rate????def?set_num_iterations(self,?num_iterations):????????"""設置迭代次數"""????????self.num_iterations?=?num_iterations????def?set_xy(self,?input,?expected_output):????????"""設置神經網絡的輸入和期望的輸出"""????????self.x?=?input????????self.y?=?expected_output????def?init_w_and_b(self):????????"""????????函數:????????????初始化神經網絡所有參數????????輸入:????????????layers_strcuture:?神經網絡的結構,例如[2,4,3,1],4層結構:????????????????第0層輸入層接收2個數據,第1層隱藏層4個神經元,第2層隱藏層3個神經元,第3層輸出層1個神經元????????返回:?神經網絡各層參數的索引表,用來定位權值?w???和偏置?b?,i為網絡層編號????????"""????????np.random.seed(3)????????#?當前神經元層的權值為?n_i?x?n_(i-1)的矩陣,i為網絡層編號,n為下標i代表的網絡層的節點個數????????#?例如[2,4,3,1],4層結構:第0層輸入層為2,那么第1層隱藏層神經元個數為4????????#?那么第1層的權值w是一個?4x2?的矩陣,如:????????#????w1?=?array([?[-0.96927756,?-0.59273074],????????#?????????????????[?0.58227367,??0.45993021],????????#?????????????????[-0.02270222,??0.13577601],????????#?????????????????[-0.07912066,?-1.49802751]?])????????#?當前層的偏置一般給0就行,偏置是個1xn?的矩陣,n?為第i層的節點個數,例如第1層為4個節點,那么:????????#????b1?=?array([?0.,??0.,??0.,??0.])????????for?l?in?range(1,?self.layers_num):????????????self.w["w"?+?str(l)]?=?np.random.randn(self.layers_strcuture[l],?self.layers_strcuture[l-1])/np.sqrt(self.layers_strcuture[l-1])????????????self.b["b"?+?str(l)]?=?np.zeros((self.layers_strcuture[l],?1))????????return?self.w,?self.b????def?layer_activation_forward(self,?x,?w,?b,?activation_choose):????????"""????????函數:????????????網絡層的正向傳播????????輸入:????????????x:?當前網絡層輸入(即上一層的輸出),一般是所有訓練數據,即輸入矩陣????????????w:?當前網絡層的權值矩陣????????????b:?當前網絡層的偏置矩陣????????????activation_choose:?選擇激活函數?"sigmoid",?"relu",?"tanh"????????返回:????????????output:?網絡層的激活輸出????????????cache:?緩存該網絡層的信息,供后續使用:?(x,?w,?b,?input_sum)?->cache"""#對輸入求加權和,見式(5.1)input_sum=np.dot(w,x)+b#對輸入加權和進行激活輸出output,_=activated(activation_choose,input_sum)returnoutput,(x,w,b,input_sum)defforward_propagation(self,x):"""函數:神經網絡的正向傳播輸入:返回:output:正向傳播完成后的輸出層的輸出caches:正向傳播過程中緩存每一個網絡層的信息:(x,w,b,input_sum),...->caches"""caches=[]#作為輸入層,輸出=輸入output_prev=x#第0層為輸入層,只負責觀察到輸入的數據,并不需要處理,正向傳播從第1層開始,一直到輸出層輸出為止#range(1,n)=>[1,2,...,n-1]L=self.param_layers_numforlinrange(1,L):#當前網絡層的輸入來自前一層的輸出input_cur=output_prevoutput_prev,cache=self.layer_activation_forward(input_cur,self.w["w"+str(l)],self.b["b"+str(l)],"tanh")caches.append(cache)output,cache=self.layer_activation_forward(output_prev,self.w["w"+str(L)],self.b["b"+str(L)],"sigmoid")caches.append(cache)returnoutput,cachesdefshow_caches(self,caches):"""顯示網絡層的緩存參數信息"""i=1forcacheincaches:print("%dtdLayer"%i)print("input:%s"%cache[0])print("w:%s"%cache[1])print("b:%s"%cache[2])print("input_sum:%s"%cache[3])print("----------")i+=1defcompute_error(self,output):"""函數:計算檔次迭代的輸出總誤差輸入:返回:"""m=self.y.shape[1]#計算誤差,見式(5.5):E=Σ1/2(期望輸出-實際輸出)2#error=np.sum(0.5*(self.y-output)**2)/m#交叉熵作為誤差函數error=-np.sum(np.multiply(np.log(output),self.y)+np.multiply(np.log(1-output),1-self.y))/merror=np.squeeze(error)returnerrordeflayer_activation_backward(self,derror_wrt_output,cache,activation_choose):"""函數:網絡層的反向傳播輸入:derror_wrt_output:誤差關于輸出的偏導cache:網絡層的緩存信息(x,w,b,input_sum)activation_choose:選擇激活函數"sigmoid","relu","tanh"返回:梯度信息,即derror_wrt_output_prev:反向傳播到上一層的誤差關于輸出的梯度derror_wrt_dw:誤差關于權值的梯度derror_wrt_db:誤差關于偏置的梯度"""input,w,b,input_sum=cacheoutput_prev=input#上一層的輸出=當前層的輸入;注意是'輸入'不是輸入的加權和(input_sum)m=output_prev.shape[1]#m是輸入的樣本數量,我們要取均值,所以下面的求值要除以m#實現式(5.13)->誤差關于權值w的偏導數derror_wrt_dinput=activated_back_propagation(activation_choose,derror_wrt_output,input_sum)derror_wrt_dw=np.dot(derror_wrt_dinput,output_prev.T)/m#實現式(5.32)->誤差關于偏置b的偏導數derror_wrt_db=np.sum(derror_wrt_dinput,axis=1,keepdims=True)/m#為反向傳播到上一層提供誤差傳遞,見式(5.28)的(Σδ·w)部分derror_wrt_output_prev=np.dot(w.T,derror_wrt_dinput)returnderror_wrt_output_prev,derror_wrt_dw,derror_wrt_dbdefback_propagation(self,output,caches):"""函數:神經網絡的反向傳播輸入:output:神經網絡輸caches:所有網絡層(輸入層不算)的緩存參數信息[(x,w,b,input_sum),...]返回:grads:返回當前迭代的梯度信息"""grads={}L=self.param_layers_num#output=output.reshape(output.shape)#把輸出層輸出輸出重構成和期望輸出一樣的結構expected_output=self.y#見式(5.8)#derror_wrt_output=-(expected_output-output)#交叉熵作為誤差函數derror_wrt_output=-(np.divide(expected_output,output)-np.divide(1-expected_output,1-output))#反向傳播:輸出層->隱藏層,得到梯度:見式(5.8),(5.13),(5.15)current_cache=caches[L-1]#取最后一層,即輸出層的參數信息grads["derror_wrt_output"+str(L)],grads["derror_wrt_dw"+str(L)],grads["derror_wrt_db"+str(L)]=self.layer_activation_backward(derror_wrt_output,current_cache,"sigmoid")#反向傳播:隱藏層->隱藏層,得到梯度:見式(5.28)的(Σδ·w),(5.28),(5.32)forlinreversed(range(L-1)):current_cache=caches[l]derror_wrt_output_prev_temp,derror_wrt_dw_temp,derror_wrt_db_temp=self.layer_activation_backward(grads["derror_wrt_output"+str(l+2)],current_cache,"tanh")grads["derror_wrt_output"+str(l+1)]=derror_wrt_output_prev_tempgrads["derror_wrt_dw"+str(l+1)]=derror_wrt_dw_tempgrads["derror_wrt_db"+str(l+1)]=derror_wrt_db_tempreturngradsdefupdate_w_and_b(self,grads):"""函數:根據梯度信息更新w,b輸入:grads:當前迭代的梯度信息返回:"""#權值w和偏置b的更新,見式:(5.16),(5.18)forlinrange(self.param_layers_num):self.w["w"+str(l+1)]=self.w["w"+str(l+1)]-self.learning_rate*grads["derror_wrt_dw"+str(l+1)]self.b["b"+str(l+1)]=self.b["b"+str(l+1)]-self.learning_rate*grads["derror_wrt_db"+str(l+1)]deftraining_modle(self):"""訓練神經網絡模型"""np.random.seed(5)foriinrange(0,self.num_iterations):#正向傳播,得到網絡輸出,以及每一層的參數信息output,caches=self.forward_propagation(self.x)#計算網絡輸出誤差cost=self.compute_error(output)#反向傳播,得到梯度信息grads=self.back_propagation(output,caches)#根據梯度信息,更新權值w和偏置bself.update_w_and_b(grads)#當次迭代結束,打印誤差信息ifself.print_costandi%1000==0:print("Costafteriteration%i:%f"%(i,cost))ifself.print_costandi%1000==0:self.costs.append(cost)#模型訓練完后顯示誤差曲線ifFalse:plt.plot(np.squeeze(self.costs))plt.ylabel(u'神經網絡誤差',fontproperties=font)plt.xlabel(u'迭代次數(*100)',fontproperties=font)plt.title(u"學習率="+str(self.learning_rate),fontproperties=font)plt.show()returnself.w,self.bdefpredict_by_modle(self,x):"""使用訓練好的模型(即最后求得w,b參數)來決策輸入的樣本的結果"""output,_=self.forward_propagation(x.T)output=output.Tresult=output/np.sum(output,axis=1,keepdims=True)returnnp.argmax(result,axis=1)defplot_decision_boundary(xy,colors,pred_func):#xy是坐標點的集合,把集合的范圍算出來#加減0.5相當于擴大畫布的范圍,不然畫出來的圖坐標點會落在圖的邊緣,逼死強迫癥患者x_min,x_max=xy[:,0].min()-0.5,xy[:,0].max()+0.5y_min,y_max=xy[:,1].min()-0.5,xy[:,1].max()+0.5#以h為分辨率,生成采樣點的網格,就像一張網覆蓋所有顏色點h=.01xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))#把網格點集合作為輸入到模型,也就是預測這個采樣點是什么顏色的點,從而得到一個決策面Z=pred_func(np.c_[xx.ravel(),yy.ravel()])Z=Z.reshape(xx.shape)#利用等高線,把預測的結果畫出來,效果上就是畫出紅藍點的分界線plt.contourf(xx,yy,Z,cmap=plt.cm.Spectral)#訓練用的紅藍點點也畫出來plt.scatter(xy[:,0],xy[:,1],c=colors,marker='o',cmap=plt.cm.Spectral,edgecolors='black')if__name__=="__main__":plt.figure(figsize=(16,32))#用sklearn的數據樣本集,產生2種顏色的坐標點,noise是噪聲系數,噪聲越大,2種顏色的點分布越凌亂xy,colors=sklearn.datasets.make_moons(60,noise=1.0)#因為點的顏色是1bit,我們設計一個神經網絡,輸出層有2個神經元。#標定輸出[1,0]為紅色點,輸出[0,1]為藍色點expect_output=[]forcincolors:ifc==1:expect_output.append([0,1])else:expect_output.append([1,0])expect_output=np.array(expect_output).T#設計3層網絡,改變隱藏層神經元的個數,觀察神經網絡分類紅藍點的效果hidden_layer_neuron_num_list=[1,2,4,10,20,50]fori,hidden_layer_neuron_numinenumerate(hidden_layer_neuron_num_list):plt.subplot(5,2,i+1)plt.title(u'隱藏層神經元數量:%d'%hidden_layer_neuron_num,fontproperties=font)nn=NeuralNetwork([2,hidden_layer_neuron_num,2],True)#輸出和輸入層都是2個節點,所以輸入和輸出的數據集合都要是nx2的矩陣nn.set_xy(xy.T,expect_output)nn.set_num_iterations(30000)nn.set_learning_rate(0.1)w,b=nn.training_modle()plot_decision_boundary(xy,colors,nn.predict_by_modle)plt.show()
2. 曬圖曬圖!
關于誤差曲線(這里只舉其中一個栗子):
通過看誤差曲線,可以從一定程度上判定網絡的效果,模型訓練是否能收斂,收斂程度如何,都可以從誤差曲線對梯度下降的過程能見一二。
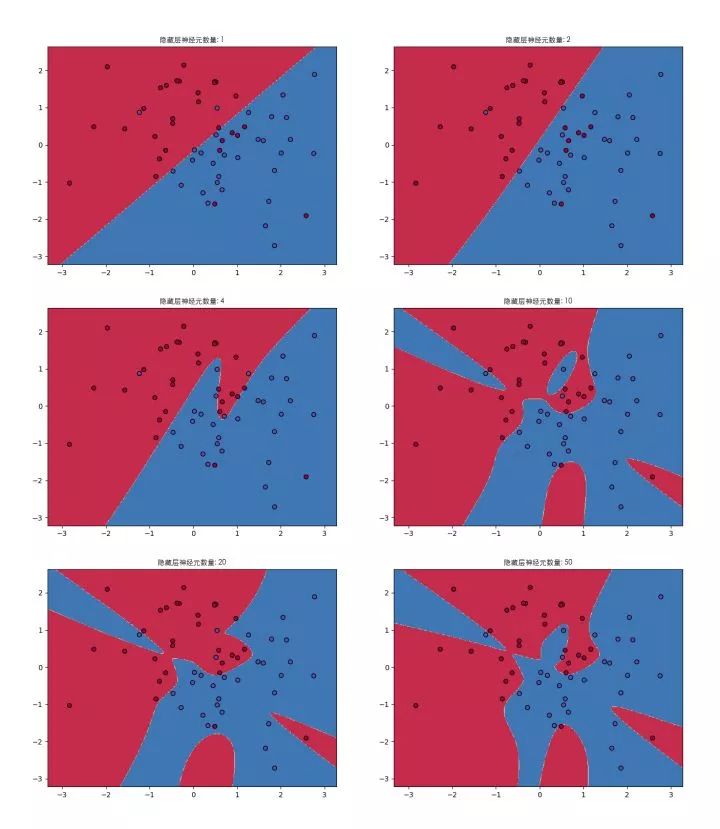
3層網絡的結構下,隱藏層只有一層,看圖說明一下隱藏層神經元個數變化對神經網絡表達能力的影響:
當隱藏層只有1個神經元:就像文章剛開始說的,一個神經元,就是個線性分類器,表達能力就一條直線而已,見式(3.6)
2個神經元:線開始有點彎曲了,但是這次結果一點都不明顯,尷尬。但從原理上神經網絡開始具備了非線性表達能力
隨著隱藏層神經元個數不斷增加,神經網絡表達能力越來越強,分類的效果越來越好。當然也不是神經元越多越好,可以開始考慮深度網絡是不是效果更好一些。
▌7. 沒有結局
記住一點,bp神經網絡是其他各種神經網絡中最簡單的一種。只有學會了它,才能以此為基礎展開對其他更復雜的神經網絡的學習。
雖然推導了并實現了算法,但是仍然是有很多疑問,這里就作為拋磚引玉吧:
神經網絡的結構,即幾層網絡,輸入輸出怎么設計才最有效?
數學理論證明,三層的神經網絡就能夠以任意精度逼近任何非線性連續函數。那么為什么還需要有深度網絡?
在不同應用場合下,激活函數怎么選擇?
學習率怎么怎么選擇?
訓練次數設定多少訓練出的模型效果更好?
AI,從入門到放棄,首篇結束。
-
函數
+關注
關注
3文章
4305瀏覽量
62430 -
神經元
+關注
關注
1文章
363瀏覽量
18438
原文標題:AI從入門到放棄:BP神經網絡算法推導及代碼實現筆記
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 神經元和函數算法之間的關系(干貨)
神經元和函數算法之間的關系(干貨)











評論